Exponential- und Logarithmusfunktionen – Kurvendiskussion
Definitionsbereich, Wertebereich, Nullstellen, Symmetrie, Extrema, Wendepunkte, Verhalten im Unendlichen, Schnittpunkt y-Achse, Sattelpunkte, Graph
Inhaltsverzeichnis zum Thema
- Einleitung
- Kurvendiskussion einer Exponentialfunktion
- Definitionsbereich
- Symmetrie
- Achsenschnittpunkte
- Extrema
- Wendepunkte
- Verhalten im Unendlichen
- Graph
- Monotonieverhalten
Einleitung
Die Untersuchung einer Funktion im Bereich der Analysis erfolgt über eine Kurvendiskussion und orientiert sich an folgenden Kriterien:
- Definitionsbereich
- Symmetrie
- Nullstellen / Achsenschnittpunkte
- Extrema
- Wendepunkte
- Verhalten im Unendlichen
- Graph
- Monotonieverhalten
Kurvendiskussion einer Exponentialfunktion
Exemplarisch untersuchen wir im Weiteren folgende Funktion bezüglich der oben genannten Kriterien:
$f(x) = xe^{-x^{2}}$
Das Vorgehen lässt sich auf andere Funktionen entsprechend übertragen.
Definitionsbereich
Um den Definitionsbereich dieser Funktion zu bestimmen, überlegen wir, welche $x$-Werte eingesetzt werden dürfen. Wir stellen im Bereich der reellen Zahlen keine Einschränkung fest, sodass der Definitionsbereich wie folgt lautet:
$\mathbb{D} = \mathbb{R}$
Symmetrie
Wir unterscheiden die Achsensymmetrie von der Punktsymmetrie. Bei der Achsensymmetrie verläuft der Graph symmetrisch zur $y$-Achse. Eine achsensymmetrische Funktion erfüllt folgende Bedingung:
$f(x) = f(-x)$
Diese überprüfen wir nun für die betrachtete Exponentialfunktion. Wir erhalten:
$f(x) = x\cdot e^{-x^{2}} \neq -x\cdot e^{-(-x)^{2}}=f(-x)$
Da die Funktion nicht achsensymmetrisch ist, untersuchen wir sie auf Punktsymmetrie. Eine Funktion ist punktsymmetrisch zum Koordinatenursprung, wenn sie folgende Bedingung erfüllt:
$f(x) = -f(-x)$
Für die Funktion ergibt sich durch Einsetzen:
$-f(-x) = - (-x)\cdot e^{-(-x)^{2}} = x\cdot e^{-x^{2}}=f(x)$
Da $f(x)=-f(-x)$ gilt, schließen wir auf Punktsymmetrie.
Achsenschnittpunkte
Der Graph kann sowohl die $x$-Achse als auch die $y$-Achse schneiden. Die $x$-Werte der Schnittpunkte mit der $x$-Achse werden auch Nullstellen genannt. Wir ermitteln die Nullstellen, indem wir die Funktionsgleichung mit $0$ gleichsetzen, also als Funktionswert $0$ annehmen. Es folgt dann:
$f(x) =x\cdot e^{-x^{2}}=0$
Ein Produkt wird Null, wenn einer der Faktoren Null ist. Da eine $e$-Funktion niemals den Wert Null annimmt, erhalten wir nur folgende Nullstelle:
$x = 0$
Der $x$-Achsenschnittpunkt ist also bei $N (0|0)$. Daraus ergibt sich auch der Schnittpunkt mit der $y$-Achse. Dem Punkt $N(0|0)$ können wir nämlich entnehmen, dass für $x=0$ der Funktionswert $y = 0$ folgt.
Folglich verläuft die Funktion durch den Koordinatenursprung.
Extrema
Um die Hoch- bzw. Tiefpunkte der Funktion zu ermitteln, ist es zunächst hilfreich, die Ableitungen zu bestimmen.
Die erste Ableitung bilden wir unter Anwendung der Produktregel. Diese lautet wie folgt:
$\left(u\cdot v\right)'=u' \cdot v + v' \cdot u$
In unserem Fall entspricht $x$ dem Faktor $u$ und $e^{-x^{2}}$ dem Faktor $v$. Zum Ableiten von $v=e^{-x^{2}}$ brauchen wir ferner die Kettenregel für die innere und äußere Ableitung:
$f'(x) = 1\cdot e^{-x^{2}} + x\cdot (-2x)\cdot e^{-x^{2}}$
Mithilfe des Distributivgesetzes können wir diesen Ausdruck wie folgt durch Ausklammern vereinfachen:
$f'(x) = e^{-x^{2}}\cdot (1 - 2x^{2})$
Die zweite Ableitung bestimmen wir durch Ableiten der ersten Ableitung. Auch hier wenden wir wieder die Ketten- und Summenregel an:
$\begin{array}{lll} f''(x) &=& -2x\cdot e^{-x^{2}}\cdot (1 - 2x^{2}) + e^{-x^{2}} \cdot (-4x) \\ &=& e^{-x^{2}}\cdot (-6x + 4x^{3}) \end{array}$
Ebenso gehen wir vor, um die dritte Ableitung zu bestimmen:
$\begin{array}{lll} f'''(x) &=&−2x\cdot e^{−x^{2}}\cdot (−6x+4x^{3}) + e^{−x^{2}}\cdot (−6+12x^{2}) \\ &=& e^{−x^{2}}\cdot (−8x^{4}+24x^{2}−6) \end{array}$
Um die Extremstellen zu berechnen, orientieren wir uns an den notwendigen und hinreichenden Bedingungen. Die notwendige Bedingung für die Existenz eines Extremums lautet:
$f'(x)=0$
Die Tangente in einem Hoch- beziehungsweise Tiefpunkt ist nämlich waagerecht, also parallel zur $x$-Achse, sodass die erste Ableitung, welche die Steigung des Funktionsgraphen in jedem Punkt beschreibt, in diesem Punkt gleich Null sein muss. Folglich setzen wir die erste Ableitung gleich Null und ermitteln die Extremstellen der Funktion:
$e^{−x^{2}}\cdot (1−2x^{2}) = 0$
Da der erste Faktor nicht Null werden kann, berechnen wir:
$\begin{array}{lll} 1 - 2x^{2} &=& 0\\ 1 &=& 2x^{2}\\ \frac{1}{2} &=& x^{2} \end{array}$
Durch das Ziehen der Wurzel erhalten wir die beiden Lösungen
$x_1 = \frac{1}{\sqrt2} \\ x_2 = -\frac{1}{\sqrt2}$
Die hinreichende Bedingung für die Existenz eines Extremums lautet:
$f''(x)\neq 0$
Wenn also die erste Ableitung gleich Null und die zweite Ableitung an der gleichen Stelle ungleich Null ist, dann handelt es sich bei der ermittelten Stelle um ein Extremum. Wir setzen in die zweite Ableitung zunächst den Wert $x_1$ ein:
$\begin{array}{lll} f''(x_{1}) &=& f''(\frac{1}{\sqrt2}) \\ &=& e^{-\left(\frac{1}{\sqrt2}\right)^{2}}\cdot (-6\cdot \frac{1}{\sqrt2} + 4\cdot\left(\frac{1}{\sqrt2}\right)^{3})\\ &=& -\frac{4}{\sqrt2}\cdot e^{-\frac{1}{2}} \lt 0 \end{array}$
Da die zweite Ableitung kleiner als Null ist, handelt es sich um ein Maximum. Den Funktionswert zu diesem Punkt bekommen wir durch Einsetzen von $x_1$ in die Ausgangsfunktion $f$:
$\begin{array}{lll} f(\frac{1}{\sqrt2})&=& \frac{1}{\sqrt2}\cdot e^{-\left(\frac{1}{\sqrt2}\right)^{2}}\\ &=&\frac{1}{\sqrt2}\cdot e^{-\frac{1}{2}} \end{array}$
Der Hochpunkt dieser Funktion liegt also bei $H(\frac{1}{\sqrt2} | \frac{1}{\sqrt2}\cdot e^{-\frac{1}{2}})$. Genauso verfahren wir mit dem Punkt $x_{2}$:
$\begin{array}{lll} f''(x_{2}) &=& f''(-\frac{1}{\sqrt2}) \\ &=& e^{-\left(-\frac{1}{\sqrt2}\right)^{2}}\cdot (-6\cdot \left(-\frac{1}{\sqrt2}\right) + 4\cdot\left(-\frac{1}{\sqrt2}\right)^{3})\\ &=& \frac{4}{\sqrt2}\cdot e^{-\frac{1}{2}} \gt 0 \end{array}$
Da die zweite Ableitung größer als Null ist, handelt es sich um ein Minimum. Den Funktionswert zu diesem Punkt erhalten wir durch Einsetzen in die Ausgangsfunktion:
$\begin{array}{lll} f(-\frac{1}{\sqrt2}) &=& -\frac{1}{\sqrt 2}\cdot e^{-\left(-\frac{1}{\sqrt2}\right)^{2}}\\ &=&-\frac{1}{\sqrt2}\cdot e^{-\frac{1}{2}} \end{array}$
Der Tiefpunkt dieser Funktion liegt bei $T(-\frac{1}{\sqrt2}| -\frac{1}{\sqrt2}\cdot e^{-\frac{1}{2}})$.
Betrachtet man die Koordinaten des Hoch- und Tiefpunktes, lassen sich die entgegengesetzten Vorzeichen durch die Punktsymmetrie erklären.
Wendepunkte
Wie schon bei den Extrema beachten wir bei der Ermittlung der Wendepunkte die notwendigen und hinreichenden Bedingungen.
Die notwendige Bedingung für die Existenz eines Wendepunktes lautet:
$f''(x) = 0$
Wir erhalten also:
$f''(x) = e^{-x^{2}} \cdot (-6x + 4x^{3}) = 0$
Da $e^{-x^{2}}\neq 0$, betrachten wir die Gleichung $-6x + 4x^{3}=0$. Es handelt sich hierbei um eine Gleichung dritten Grades, die wir durch Ausklammern von $x$ wie folgt vereinfachen können:
$x(-6 + 4x^{2}) = 0$
Laut dem Satz vom Nullprodukt wird ein Produkt Null, wenn einer der Faktoren Null ist. Daraus ergibt sich: $x_1 = 0$ oder $-6 + 4x^{2} = 0$
$\begin{array}{llll} -6 + 4x^{2} &=& 0 & \vert +6\\ 4x^{2} &=& 6 & \vert :4\\ x^{2} &=& \frac{3}{2} & \end{array}$
Wir ziehen die Wurzel und erhalten zusätzlich zu $x_1=0$ die beiden Lösungen
$x_2 = \sqrt\frac{3}{2} \\ x_3 = - \sqrt\frac{3}{2}$
Die hinreichende Bedingung für die Existenz eines Wendepunktes lautet:
$f'''(x)\neq 0$
Durch Einsetzen der ermittelten Werte überprüfen wir diese Bedingung. Wir erinnern uns an unsere dritte Ableitung:
$f'''(x) = e^{−x^{2}}\cdot(−8x^{4}+24x^{2}−6)$
Für die ermittelten Werte erhalten wir:
$ f'''(0) \neq 0 \\ f'''(\sqrt\frac{3}{2}) \neq 0 \\ f'''(- \sqrt\frac{3}{2}) \neq 0 $
Nun bestimmen wir noch die zugehörigen Funktionswerte. Wir kennen bereits den Punkt $(0|0)$ des Funktionsgraphen, hier haben wir also den ersten Wendepunkt $W_1(0|0)$. Die beiden übrigen Wendepunkte sind wie folgt gegeben:
$\begin{array}{lll} f(\sqrt\frac{3}{2}) &=& \sqrt\frac{3}{2}\cdot e^{-\left(\sqrt\frac{3}{2}\right)^{2}} \\ &=& \sqrt\frac{3}{2}\cdot e^{-\frac{3}{2}} \end{array}$
Für den zweiten Wendepunkt ergibt sich $W_{2}(\sqrt\frac{3}{2} | \sqrt\frac{3}{2}\cdot e^{-\frac{3}{2}})$. Aufgrund der Punktsymmetrie können wir nun auf den dritten Wendepunkt schließen, dieser liegt in $W_{3}(-\sqrt\frac{3}{2} | -\sqrt\frac{3}{2}\cdot e^{-\frac{3}{2}})$.
Verhalten im Unendlichen
Wir untersuchen das Verhalten für betragsmäßig große $x$-Werte, also das Globalverhalten $|x| \rightarrow \infty$.
Was passiert, wenn in die Funktion sehr große und sehr kleine Werte eingesetzt werden? Konvergieren dann die Funktionswerte zu einem bestimmten Wert oder gegen $+\infty$ beziehungsweise $-\infty$?
Unsere Funktion zerlegen wir in die beiden Faktoren $x$ und $e^{- x^{2}}$ und stellen uns vor, dass die Variable $x$ gegen $\infty$ strebt. Der erste Faktor $x$ wird dann gegen $\infty$ streben. Den zweiten Faktor schreiben wir wie folgt um:
$e^{- x^{2}}=\frac{1}{e^{x^2}}$
Dieser Faktor strebt für $x\rightarrow\infty$ gegen Null, da der Nenner immer größer und dadurch der Bruch immer kleiner wird. Das Produkt aus den Grenzwerten $\infty$ und $0$ ergibt $0$, da die Exponentialfunktion wesentlich schneller gegen Null konvergiert als die ganzrationale Funktion $x$.
Aufgrund der Punktsymmetrie verhält es sich für $x\rightarrow -\infty$ genauso. Der erste Faktor $x$ strebt gegen $-\infty$ und der zweite Faktor wieder gegen Null, sodass die Funktion insgesamt gegen Null strebt.
Dieses Streben gegen Null weist auf Asymptoten hin. Die Funktion schmiegt sich bei sehr kleinen und sehr großen $x$-Werten immer mehr an die $x$-Achse an.
Graph
Aufgrund der ermittelten Funktionseigenschaften können wir nun auf den Graphen der Funktion schließen.
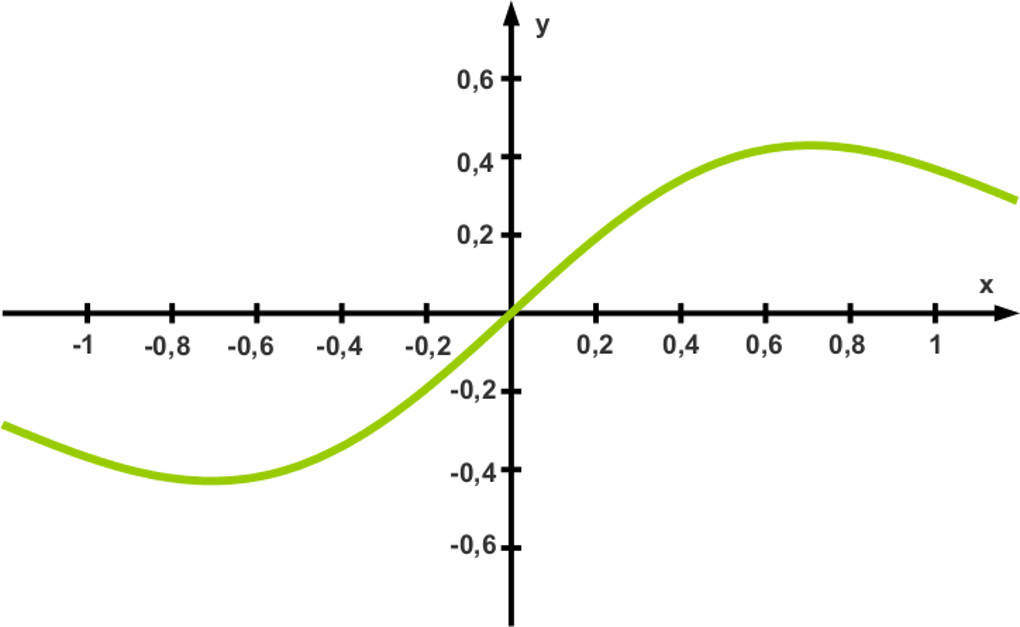
Monotonieverhalten
Anhand des Graphen erkennen wir, dass die Funktion zwischen den Extrema steigt oder fällt.
Wir interessieren uns für das Verhalten rechts von dem Hochpunkt $\frac{1}{\sqrt2}$ und untersuchen die erste Ableitung für einen $x$-Wert rechts davon, beispielsweise $x = 1$. Wir erhalten dann:
$f'(1) = e^{-1^{2}}\cdot (1 - 2) \lt 0$
Es resultiert also ein negativer Wert, welcher auf eine fallende Tangente schließen lässt. Also fällt die Ausgangsfunktion monoton rechts vom Hochpunkt.
Genauso können wir vorgehen, um zu ermitteln, wie sich die Funktion links vom Tiefpunkt verhält. Es folgt:
$f'(-1) = e^{-(-1)^{2}}\cdot (1 - 2) \lt 0$
Die erste Ableitung ist an der Stelle $x = -1$ ebenfalls negativ, also fällt die Funktion von $-\infty$ bis $\frac{-1}{\sqrt2}$ ebenfalls monoton.
Schauen wir noch auf den Bereich in der Mitte, also zwischen Tiefpunkt und Hochpunkt.
Wählen wir einen Punkt dazwischen, zum Beispiel $x = 0$. Wir können von der ersten Ableitung wieder auf das Monotonieverhalten schließen:
$f'(0) = e^{0^{2}}\cdot 1 = 1\cdot 1 = 1\gt 0$
Da die Ableitung positiv ist, steigt die Funktion zwischen dem Tief- und Hochpunkt monoton.
Alle Videos zum Thema
Videos zum Thema
Exponential- und Logarithmusfunktionen – Kurvendiskussion (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Exponential- und Logarithmusfunktionen – Kurvendiskussion (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 Exponentialfunktion – Kurvendiskussion
Exponentialfunktion – Kurvendiskussion
 Natürliche Logarithmusfunktionen – Kurvendiskussion
Natürliche Logarithmusfunktionen – Kurvendiskussion









