Massenspektrometer

Massenspektrometer Übung

• Gib an, welche Aussagen über das Massenspektrometer zutreffen.

  Tipps

  Das Massenspektrometer besteht unter anderem aus einem Geschwindigkeitsfilter.

  Nach dem Geschwindigkeitsfilter findet sich ein evakuiertes Vakuumrohr.

  Lösung

  Das Massenspektrometer beruht auf einigen wenigen physikalischen Grundannahmen.

  Zunächst müssen die betrachteten Teilchen unbedingt elektrisch geladen sein. Es kommen daher Elektronen, Protonen oder Ionen als Probekörper infrage. Neutronen oder nach außen elektrisch neutrale Elemente oder Moleküle können nicht verwendet werden. Das liegt daran, dass auf die Teilchen die Lorentzkraft wirken soll, um eine Kreisbewegung zu erzeugen und so anhand des Radius eine Aussage über die Masse machen zu können. Es wirkt also eine Kraft im Magnetfeld.

  Aufgrund dieser Kraft werden die geladenen Teilchen auf eine Kreisbahn bewegt und letztendlich auf eine Photoplatte geschossen. Je nach Auftreffpunkt kann man nun bestimmen, wie schwer das auftreffende Teilchen sein musste.

  Wichtig ist dabei, dass im Inneren des Massenspektrometers ein Vakuum herrscht. Andernfalls treffen die beschleunigten Ionen, schon bevor sie auf die Photoplatte treffen, auf Gasmolekühle, sodass keine Messung mehr möglich wäre.

• Bezeichne den Aufbau des Massenspektrometers.

  Tipps

  Unter Einwirkung der Lorentzkraft verlaufen die Ionen auf einer Kreisbahn.

  Die Lorentzkraft wirkt auf bewegte Ladungsträger.

  Den Kondensator mit angelegtem Magnetfeld können nur Ionen mit bestimmter Geschwindigkeit passieren.

  Die Messung muss im Vakuum stattfinden.

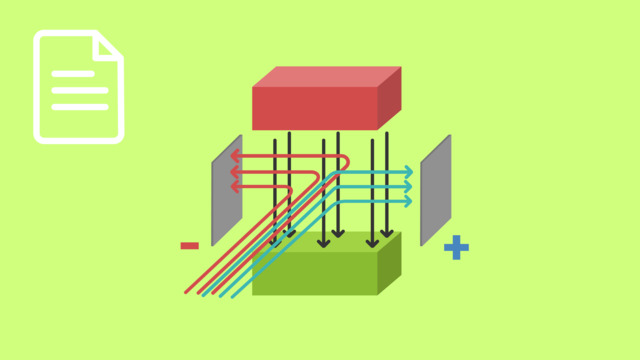
  Lösung

  Das Massenspektrometer besteht im Wesentlichen aus vier Bauteilen, die innerhalb eines evakuierten Raumes angebracht sind.

  Das erste Bauteil ist eine Ionenquelle. Diese erzeugt freie Ionen, indem etwa eine Heizspule unter Spannung gesetzt wird. Diese freien, geladenen Teichen werden beschleunigt und durch einen Geschwindigkeitsfilter gelenkt. Dieser Filter ist das zweite Bauteil. Diesen können nur Ionen bestimmter Geschwindigkeit passieren. Aufgrund des elektrischen Feldes werden zu langsame Ionen zu den Platten des Kondensators abgelenkt. Ionen, die zu schnell sind, werden aufgrund der Lorentzkraft ausgesiebt.

  Die Ionen, welche den Filter passieren, gelangen durch eine Blende in den zweiten Teil des Massenspektrometers. Hier sind die Ionen wieder einem magnetischen Feld ausgesetzt, sozusagen dem dritten Bauteil des Messgerätes. Auch hier wirkt die Lorentzkraft und die Ionen werden auf eine Kreisbahn gelenkt. Der Radius der Kreisbahn ist dabei äquivalent zur Masse der Ionen. Auf einer Photoplatte, dem vierten Bauteil, werden die Ionen detektiert. So kann der Radius der Kreisbewegung genau ermittelt und schlussendlich mit dem Ansatz $m = \frac{q \cdot B' \cdot r}{v} $ bestimmt werden.

  Die Messung muss dabei im Vakuum stattfinden. Andernfalls würden die Ionen mit den Gasmolekülen stoßen und ihre Bewegungsenergie verlieren. Eine zuverlässige Messung wäre nicht weiter möglich.

• Berechne die Geschwindigkeit der Ionen hinter dem Geschwindigkeitsfilter.

  Tipps

  Rechne in den Grundeinheiten.

  Es soll $ F_E = F_L$ sein.

  Es gilt $ q \cdot E = q \cdot v \cdot B$.

  Lösung

  In einem Geschwindigkeitsfilter steht ein Magnetfeld der Stärke $B$ senkrecht auf dem elektrischen Feld $E$ eines Kondensators.

  Bringt man nun eine beschleunigte Ladung senkrecht zu $B$ und $E$ in den Geschwindigkeitsfilter ein, so wirken auf den Probekörper zum einen die Kraft $ F_E = q \cdot E $ aus der elektrischen Anziehung des elektrischen Feldes sowie die Lorentzkraft $ F_L = q \cdot v \cdot B$.

  Nur, wenn sich die beiden Kräfte im Gleichgewicht befinden, kann ein Teilchen den Filter passieren.

  Setzen wir also $ F_E = F_L$. Damit ist $ q \cdot E = q \cdot v \cdot B$. Nun kürzen wir das $q$ weg und erhalten : $ E = v \cdot B $. Umgestellt nach $v$ ergibt sich nun $ v = \frac{E}{B} $.

  Die Filterwirkung hängt also nur von der Stärke des elektrischen Feldes und der Magnetfeldstärke ab.

  Für einen Filter mit : $ E =1,45~\frac{\text{kV}}{\text{m}} $ und $B = 278~\text{mT}$ ergibt sich $ v = \frac{E}{B} = \frac{1{,}45~\frac{\text{kV}}{\text{m}}}{278~\text{mT}} = \frac{1450~\frac{\text{V}}{\text{m}}}{0{,}278~\text{T}} =5\,215{,}83~\frac{\text{m}}{\text{s}}$.

  Achte bei der Berechnung unbedingt darauf, in den Grundeinheiten zu rechnen.

• Berechne die Massen.

  Tipps

  $ v = \frac{E}{B} $

  Rechne in den Grundeinheiten.

  $m = \frac{q \cdot r \cdot B' \cdot B}{E}$

  Lösung

  Um die Masse eines Teilchens zu berechnen, welches auf die Photoplatte des Massenspektrometers aufgetroffen ist, müssen wir zunächst einmal dessen Ladung und Geschwindigkeit kennen. Zudem müssen wir das an der Vakuumröhre angelegte Magnetfeld kennen sowie den Radius der Kreisbewegung.

  Sind diese Größen bekannt, so können wir die Formel $m = \frac{q \cdot r \cdot B' \cdot B}{E}$ anwenden.

  Doch wo finden wir hier die Geschwindigkeit? Im Massenspektrometer ist ein sogenannter Geschwindigkeitsfilter integriert. Dieser besteht aus einem Kondensator, auf den ein ausgerichtetes Magnetfeld wirkt. Tritt nun ein geladenes Teilchen hindurch, wird dieses entweder vom magnetischen oder elektrischen Feld abgelenkt oder diese beiden Wirkungen heben sich auf und das Teilchen passiert den Filter. So kann sichergestellt werden, dass nur Teilchen mit einer bestimmten Geschwindigkeit in die Vakuumröhre des Massenspektrometers eintreten. Es gilt der Zusammenhang $v = \frac{E}{B}$.

  Die Teilchen, die den Geschwindigkeitsfilter passiert haben, sind nun also alle gleich schnell und werden in die Vakuumröhre eingeleitet. Hier werden sie nun durch das Magnetfeld $B'$ ausgerichtet. Dieses ist nicht gleich dem Magnetfeld im Geschwindigkeitsfilter. Als Folge der Lorentzkraft werden die geladenen Teilchen auf eine Kreisbahn gelenkt und treffen auf einer Photoplatte auf. Anhand des Auftreffpunkts kann nun der Radius der Kreisbewegung $r$ abgemessen werden. Nun kann man alle Größen einsetzen und erhält als Ergebnis die Masse des untersuchten Teilchens.

  Betrachten wir ein Beispiel: Ein Ion mit doppelter Einheitsladung $e$ tritt einen Geschwindigkeitsfilter mit $E = 1{,}1~\frac{\text{kV}}{\text{m}}$ und $B = 5~\text{mT}$. In der anschließenden Vakuumröhre herrscht ein Magnetfeld von $B' = 32{,}2~\text{T}$. Der Radius der Kreisbahn wird zu $ r = 7{,}7~\text{mm}$ bestimmt.

  Wir setzen in $m = \frac{q \cdot r \cdot B' \cdot B}{E}$ ein und erhalten so $m = \frac{3{,}2 \cdot 10^{-19} \cdot 0{,}0077~\text{mm} \cdot 32{,}2~\text{T} \cdot 0{,}005~\text{T}}{1\,100~\frac{\text{V}}{\text{m}}}$.

  Als Ergebnis erhalten wir nun $m = 3{,}61 \cdot 10^{-25}~\text{kg}$.

• Gib die Funktion des Massenspektrometers an.

  Tipps

  Es wirkt die Lorentzkraft.

  Die Lorentzkraft wirkt auf bewegte Ladungsträger.

  Lösung

  Das Massenspektrometer ist, wie der Name schon vermuten lässt, ein Messgerät zur Bestimmung der Masse von Atomen und Molekülen.

  Mit Hilfe eines Geschwindigkeitsfilters werden nur Ionen, die sich mit einer bestimmen Geschwindigkeit bewegen, in eine Vakuumröhre geleitet. Hier sind sie nun ausschließlich einem magnetischen Feld ausgesetzt und werden aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt. Diese Kraft wirkt ausschließlich auf geladene Teilchen. Neutronen oder neutrale Teilchen werden also nicht beeinflusst und sind daher auch nicht messbar. Je nachdem, wie stark das Magnetfeld, wie groß die Masse des Ions und wie schnell dieses ist, trifft es an einer bestimmten Stelle auf einer Photoplatte auf. Man kann über den Radius der Kreisbewegung bestimmen, welche Masse das Ion haben muss.

  So können auch die Massen sehr leichter Teilchen bestimmt werden.

• Bestimme die fehlenden Begriffe.

  Tipps

  Isotope sind meist nur wenige Neutronenmassen leichter oder schwerer als ihre elementaren Atome.

  Der Radius der Ionenbewegung verhält sich proportional zur Ionenmasse.

  Im Geschwindigkeitsfilter gilt : $v = \frac{E}{B}$.

  Lösung

  Um die Aussagen zu überprüfen, betrachten wir zunächst den Geschwindigkeitsfilter. Nur Ionen mit einer bestimmten Geschwindigkeit können diesen passieren. Mit dem Ansatz <nobr>$v = \frac{E}{B}$</nobr> kann die Durchtrittsgeschwindigkeit ermittelt werden. Für den Fall, das $E$ und $B$ den gleichen Betrag aufweisen, ergibt sich dann mit <nobr>$E = B$</nobr> in <nobr>$v = \frac{E}{B} = \frac{E}{E} = 1~\frac{\text{m}}{\text{s}}$.</nobr> Für einen Geschwindigkeitsfilter mit <nobr>$E = 3{,}9~\frac{\text{kv}}{\text{m}}$</nobr> und <nobr>$B = 1{,}1~\text{T}$</nobr> ergibt sich aus dem gleichen Ansatz <nobr>$v = \frac{3,9~\frac{\text{kv}}{\text{m}}}{1{,}1~\text{T}} = 3\,545{,}45~\frac{\text{m}}{\text{s}}$.</nobr>

  Da die Masse eines Teilchens direkt proportional zum Radius der Ionenbahn ist, treffen schwere Teilchen weiter außen auf als leichtere. Das ist damit zu erklären, dass der Radius der Ionenbahn zunimmt und der Abstand zwischen Blende und Auftreffpunkt ebenfalls steigt.

  Haben Teilchen ähnliche Massen, wie es bei den Isotopen einer Atomart der Fall ist, treffen diese logischerweise nah beieinander auf der Photoplatte auf. Auch hier liegt die Proportionalität von Radius und Masse zugrunde. Isotope sind ja nur ein wenig leichter oder schwerer als ihre elementaren Ionen, denn der Gewichtsunterschied besteht meist in wenigen Neutronenmassen.

  Du siehst: Mit einigen simplen Ansätzen lassen sich auch relativ komplexe Fragestellungen zum Massenspektrometer leicht beantworten.