Synchrotron

Videos
anschauen

Übungen
starten

Arbeitsblätter
anzeigen

Lehrer*innen
fragen

Du willst ganz einfach ein neues Thema lernen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?

5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.

92%

der Schüler*innen hilft sofatutor beim selbstständigen Lernen.
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.

93%

der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert.
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.

94%

der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Noch nicht angemeldet? 30 Tage kostenlos testen

Bewertung

Gib eine Bewertung ab!

Du musst eingeloggt sein, um bewerten zu können.

Wow, Danke!
Gib uns doch auch deine Bewertung bei Google! Wir freuen uns!

Zu Google

Die Autor*innen

Kalo

Synchrotron

lernst du in der 11. Klasse - 12. Klasse - 13. Klasse

Grundlagen zum Thema Synchrotron

In diesem Video lernst du, was man unter einem Synchrotron versteht. Das Synchrotron ist ein Teilchenbeschleuniger, der geladenen Teilchen eine hohe Geschwindigkeit (hohe kinetische Energie) verleiht, ganz ähnlich wie ein Zyklotron. Die Teilchen werden in einem Ringtunnel (Torus) mit elektrischen Wechselfeldern beschleunigt und dabei mit Magnetfeldern auf einer Bahn in der Mitte des Torus gehalten. Magnetfeld und elektrisches Wechselfeld werden synchron an die Änderung der Geschwindigkeit und der relativistischen Masse der beschleunigten Teilchen angepasst.

Transkript Synchrotron

Hallo und herzlich willkommen. Ich zeige hier die Prinzipien des Aufbaus eines Synchrotrons und erkläre in Grundzügen seine Funktionsweise. Du solltest mit der Bewegung von Ladungsträgern in elektrischen und magnetischen Feldern vertraut sein. Und wenn du das Video über das Zyklotron gesehen hast, dann hast du einen guten Teil der Funktionsprinzipien auch des Synchrotrons schon verstanden. Im Video über das Zyklotron war erwähnt, dass es eine Weiterentwicklung gibt, das Synchrozyklotron, das man einsetzt, wenn man eine Energie größer als 20 Megaelektronenvolt, der dafür Protonen erzielen will, ab einem Gigaelektronenvolt Energie muss man sogar zum Synchrotron übergehen. Auch hier erfolgt die Beschleunigung durch elektrische Felder und die Einlenkung des Teilchens auf eine Bahn wird durch ein Magnetfeld erzwungen. Nur ist das Konstruktiv anders aufgebaut. Denn das Hauptstück ist ein großer Ringtunnel in der Form eines Donuts, das heißt geometrisch eines Torus, der zum Beispiel am Desy in Hamburg einen Umfang von 6,3 Kilometer haben kann. Um diesen Ringtunnel herum sind in regelmäßigen Abständen Elektromagneten installiert, die sich der Bogenform des Ringes anschmiegen. Das von ihnen erzeugte magnetische Feld lässt sich so steuern, dass man ganz gezielt Teilchen verschiedener Geschwindigkeiten und verschiedener Masse genau auf der Mittelachse des Torus entlang fliegen lassen kann. Zwischen den Abschnitten mit Magneten haben wir Anordnungen elektrischer Felder, ganz wie am Spalt des Zyklotrons. Durch sie werden die geladenen Teilchen, die in den Tunnel eingeschossen wurden, weiter beschleunigt. Jetzt ist es leicht verständlich, warum hier etwas synchronisiert werden muss, denn wenn wir die Teilchen beschleunigen, erhöhen wir ihre Geschwindigkeit. Also muss auch die Radialbeschleunigung steigen, wenn wir das Teilchen auf einer Kreisbahn wieder im gegebenen Radius halten wollen. Dass wir unsere Teilchen mit magnetischen Feldern auf einer Bahn halten, heißt natürlich, dass wir die Lorentzkraft einsetzen. Wir müssen also die magnetische Feldstärke erhöhen, wenn die Bahngeschwindigkeit V erhöht wurde, aber alle anderen Größen konstant geblieben sind. Tatsächlich müssen wir die Feldstärke oder den magnetischen Fluss sogar noch stärker erhöhen, als nur durch die Steigerung der Geschwindigkeit nötig wäre. Denn wir arbeiten hier ja bei Geschwindigkeiten, die so hoch sind, dass die relativistische Massenzunahme eine bedeutende Rolle spielt. Eben das hatte schon den Übergang vom einfachen Zyklotron zum Synchrozyklotron bestimmt. Und hier erst recht. Nun muss noch dafür gesorgt werden, dass die elektrischen Felder immer dann maximale Kraft auf die Teilchen ausüben und sie beschleunigen, wenn diese Teilchen durch die Zone des Feldes laufen. Das erreicht man natürlich am besten mit einer Wechselspannung, deren Kreisfrequenz gerade der Umlaufgeschwindigkeit der Teilchen entspricht und die also auch nachgeregelt wird, wenn die Teilchen schneller werden. Natürlich gibt es noch mindestens 2 Lücken im Torus, das heißt, der Ring ist nicht ganz geschlossen. Zum einen, damit Teilchen überhaupt hineingeschossen werden können und zum anderen, um in die Bahn der beschleunigten Teilchen ein Target halten zu können und den erwünschten Effekt, die Kollision der hochenergetischen Teilchen, mit ausgesuchtem Material herbeiführen zu können. Ein solcher Beschuss dient vorwiegend der Materialuntersuchung, aber in Abhängigkeit von der Energie der Teilchen, sehr häufig auch heute noch der gezielten Kollision von Elementarteilchen, an deren nachfolgendem Zerfall durch den Aufprall, man Studien über den Aufbau der Materie durchführt. In den 80er und 90er Jahren wurde mit einem solchen Gerät das W-Boson und das Top-Quark nachgewiesen. Kurz zusammengefasst besteht also das Synchrotron aus einem ringförmigen Tunnel, in den geladene Elementarteilchen eingeschossen werden, nachfolgend durch elektrische Felder schubweise beschleunigt werden und dabei von Magnetfeldern auf die Kreisbahn des Ringtunnels gezwungen werden. Synchrotron, also synchronisierend, heißt dieses Gerät, weil wir einerseits mit dem Anwachsen der Geschwindigkeit und der Zunahme der relativistischen Masse die Magnetfelder verstärken müssen, die die Radialkraft erzeugen, um die Teilchen auf ihrer Kreisbahn zu halten. Und andererseits ebenso die Wechselspannung der elektrischen Felder, die die Beschleunigung der Teilchen bewirken nachregeln müssen, wenn die Teilchen sich schneller auf diesem Ring bewegen. Wenn du ein bisschen neugierig geworden sein solltest, dann lohnt es sich, dass du dich ein bisschen informierst, über das Forschungszentrum Desy in Hamburg, das Forschungszentrum CERN in Genf in der Schweiz oder die Anlage Soleil in Frankreich. Bis zum nächsten Video.

Synchrotron Übung

Du möchtest dein gelerntes Wissen anwenden? Mit den Aufgaben zum Video Synchrotron kannst du es wiederholen und üben.

Nenne die wichtigsten Bestandteile eines Synchrotrons.

Tipps

Im Synchrotron werden etwa Protonen oder Elektronen beschleunigt.

Die spezifische Ladung von Protonen und Elektronen ist sehr groß.

Es wirkt die Lorentzkraft.

Lösung

Damit Teilchen im Synchrotron beschleunigt werden können, sind einige Komponenten besonders wichtig.
An einem Ringtunnel sind dazu mehrere elektrische Felder angebracht.
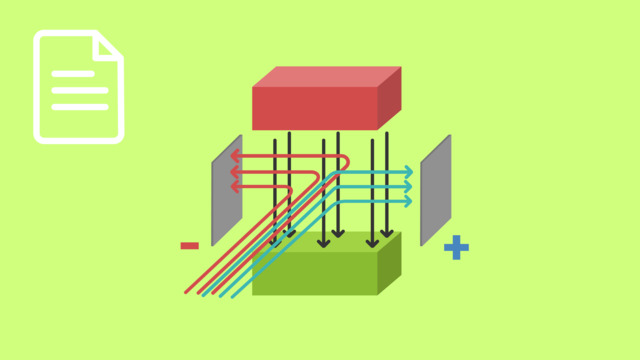
Setzen wir ein geladenes Teilchen dem elektrischen Feld aus, so wird dieses beschleunigt. Es werden nur geladene Teilchen beschleunigt, denn das elektrische Feld hat keine Auswirkung auf ungeladene Teilchen wie etwa Neutronen.
Das geladene Teilchen wird durch das elektrische Feld nun lediglich geradlinig beschleunigt. Es würde also schnell mit der Wand des Tunnels stoßen und wir könnten keine großen Geschwindigkeiten erreichen.
Es ist also eine Art Lenkung zur Kontrolle der Teilchenbewegung notwendig.
Dazu sind mehrere Elektromagneten am Ringtunnel angebracht. Diese generieren ein einstellbares, homogenes magnetisches Feld. Durchschreitet ein geladenes Teilchen, also ein elektrischer Strom, dieses Magnetfeld, so wird es aufgrund der Lorentzkraft abgelenkt. So kann es auf der Kreisbahn gehalten werden.
Das Schwerefeld der Erde spielt dabei nur eine untergeordnete Rolle. Die Kräfte, die aufgrund der Interaktion des Teilchens mit dem starken magnetischem und elektrischem Feld wirken, sind sehr sehr viel größer als jene, die aus der Teilchenmasse und dem relativ schwachen Schwerefeld der Erde resultieren.
Das wird noch klarer, wenn wir die Ladung eines Elektrons mit seiner Masse vergleichen. Dieses trägt die Elementarladung $ q = 1,6 \cdot 10^{-19} C$, wiegt dabei jedoch lediglich etwa $ m = 9,1 \cdot 10^{-31} kg$. Daraus resultiert eine große spezifische Ladung $ \frac{q}{m}$.
Aus diesem Grund können wir die Erdanziehung vernachlässigen.
Beschreibe, welche Prozesse im Synchrotron ablaufen.

Tipps

1980 wurde das W-Boson und das Top-Quark mit Hilfe des Synchrotrons nachgewiesen.

Das Synchrotron wir gebraucht, um geladene Teilchen auf sehr hohe Geschwindigkeiten zu beschleunigen.

Auf einen Strom wirkt im Magnetfeld die Lorentzkraft.

Lösung

Das Synchrotron wir gebraucht, um geladene Teilchen auf sehr hohe Geschwindigkeiten zu beschleunigen.
Dabei werden zunächst geladene Teilchen aus einer Ionenquelle in den Rohrtunnel des Zyklotrons eingeführt. Diese geladenen Teilchen sind nun zunächst einem elektrischen Feld ausgesetzt, welches der Beschleunigung dient.
Damit die beschleunigten Teilchen nun auf eine Kreisbahn gelenkt und gehalten werden können, sind einige Elektromagneten am Rohrsystem angebracht.
Das hat den Vorteil, dass die Magnetfeldstärke gut regelbar ist und man so auf eine steigende Teilchengeschwindigkeit oder relativistische Massenzunahme gut reagieren kann.
Durchläuft ein Teilchen mit der Ladung $Q$ in einer bestimmten Zeit $ \Delta t$ einen beobachteten Querschnitt, so ist per Definition $ \frac{Q}{\Delta t} = I$ also ein Strom $I$ vorhanden.
Auf einen Strom wirkt im Magnetfeld nun die Lorentzkraft. Diese lenkt die Teilchenbewegung nun auf eine Kreisbahn und der Ringtunnel des Synchrotrons kann immer wieder durchlaufen werden.
Doch wozu der ganze Aufwand?
Sobald ein Teilchen die angestrebte Geschwindigkeit erreicht hat, kann man dieses auf Kollisionskurs mit anderen Teilchen oder mit einem Target bringen.
Durch die enorm hohe Energie der sehr schnellen Bewegung der Teilchen, verlieren diese ihre atomare Struktur und man kann subatomare Beobachtungen. Dadurch kann man die Beschaffenheit der Materie besser verstehen.
So wurden mit Hilfe des Synchrotrons 1980 das W-Boson und das Top-Quark nachgewiesen.
Ordne den Komponenten des Synchrotrons ihre Wirkung zu.

Tipps

Es sollten möglichst wenige Fremdpartikel im Synchrotron vorhanden sein.

$ F_L = F_R$

Eine bewegte Ladung ist ein Strom.

Lösung

Das Synchrotron wir gebraucht, um geladene Teilchen auf sehr hohe Geschwindigkeiten zu beschleunigen.
Dazu haben unterschiedliche Komponenten ganz unterschiedliche Aufgaben. Die Anordnung in einem Ringtunnel hat den Hintergrund, dass sichergestellt werden muss, dass sich möglichst keine unerwünschten Partikel im Synchrotron befinden.
Durch die Spalten die im Tunnel angebracht sind, können nun geladene Teilchen hineingebracht oder herausgeschossen werden.
Wird ein Teilchen in das Synchrotron eingebracht, so wird dieses in einem elektrischen Feld beschleunigt.
Nun bewegt sich das Teilchen und wir können dieses als Strom definieren. Denn ein elektrischer Strom ist ja auch nichts anderes als bewegte Ladung.
Aufgrund der Magnetfeldes, welches an einigen Stellen den Ringtunnel durchfließt, wirkt die Lorentzkraft auf das Teilchen.
Durch die Lorentzkraft wird das Teilchen nun auf eine Kreisbahn gelenkt und kann den Ringtunnel immer wieder durchlaufen, und dabei immer mehr an Geschwindigkeit gewinnen.
Berechne die notwendige Stärke der Magnetfelder.

Tipps

$F_R = m \cdot \frac{v^2}{r}$

$F_L = q \cdot v \cdot B$

$B = \frac{m \cdot v}{q \cdot r}$

Lösung

Wir berechnen, wie groß ein Magnetfeld sein muss, damit ein Teilchen mit bestimmter Masse und Ladung mit einer festgelegten Geschwindigkeit auf einer bestimmten Bahn läuft.
Das heißt also, wir wollen $B$ in Abhängigkeit von $q$,$m$,$v$ und $r$ ausdrücken.
Da wir wissen, dass die Lorentzkraft wirkt und es sich um eine Kreisbewegung handelt, setzen wir die Zentripetalkraft $F_R$ mit der Lorentzkraft $F_R$ gleich.
Mit $ F_R = m \cdot \frac{v^2}{r} $ und $ F_L = q \cdot v \cdot B$ folgt also $m \cdot \frac{v^2}{r} = q \cdot v \cdot B $, und nach Umformen: $B = \frac{m \cdot v}{q \cdot r} $.
Betrachten wir ein Beispiel.
Mit der Masse $m = 9,1 \cdot 10^{-31} kg$ und der Ladung $ q = 1,6 \cdot 10^{-19} C$ sowie $r = 1250 m$ und $v = 9,1 \cdot 10^6 \frac{m}{s}$ folgt
$B = \frac{$m = 9,1 \cdot 10^{-31} kg \cdot 9,1 \cdot 10^6 \frac{m}{s}}{1,6 \cdot 10^{-19} C \cdot 1250 m} = 41,4 nT$.
Mit einem Magnetfeld der Stärke $ B = 41,4 nT$ können wir die beschriebene Bewegung des Teilchens einstellen.
Gib an, wozu die Spalten zwischen den Teilen des Ringtunnels genutzt werden.

Tipps

Mit dem Synchrotron konnte man die Existenz von subatomaren Partikeln nachweisen.

Wir nutzen geladenen Teilchen aus einer Ionenquelle.

Lösung

Die Spalten in der Betonwand des Ringtunnels sind für die Verwendung des Synchrotrons sehr wichtig.
Sie werden dazu genutzt, Teilchen in das System hineinzugeben, diese herauszuschießen oder ein Target einzubringen.
Sie stellen also sicher, dass man ein auswertbares Versuchsergebnis bekommen kann.
Betrachten wir die einzelnen Verwendungen genauer.
Bevor ein Teilchen überhaupt beschleunigt werden kann, muss dieses erst einmal in das Synchrotron hineingegeben werden, gewissermaßen müssen wir erst einmal nachladen.
Dazu schießt man geladenen Teilchen aus einer Ionenquelle durch den Spalt in das Synchrotron hinein.
Nun werden die Teilchen beschleunigt und auf eine Kreisbahn gelenkt.
Um nun ein Versuchsergebnis zu erhalten, bringt man ein Target ein. Das heißt, es werden Fremdteilchen durch einen Spalt in das Synchrotron eingebracht.
Das Target wird in die Bahn der beschleunigten Teilchen gehalten, und man kann beobachten, was beim Aufprall passiert.
Mit diesem Versuch konnte man die Existenz von subatomaren Partikeln nachweisen. Außerdem kann man Materialien prüfen, die für hohe Belastungen ausgelegt sein sollen.
Analysiere, was synchronisiert wird.

Tipps

Synchronisieren bedeutet, mehrere Komponenten aufeinander abzustimmen.

Ein Teilchen im Zyklotron beschreibt eine spiralförmige Bahn, im Synchrotron eine kreisförmige.

Die Geschwindigkeit eines Teilchens ist nicht konstant. Damit ist auch die Kreisfrequenz veränderlich.

Lösung

Der Name des Synchrotrons weist uns direkt darauf hin, dass hier etwas synchronisiert werden muss.
Synchronisieren bedeutet in diesem Zusammenhang, dass wir mehrere Komponenten aufeinander abstimmen müssen.
Steigt etwa die Geschwindigkeit eines Teilchens bei konstantem Magnetfeld, Ladung und Masse, so muss aus $ r = \frac{m \cdot v }{B \cdot q} $ der Radius größer werden.
Da dieser jedoch konstant sein muss, denn sonst würde das Teilchen ja mit der Wand der Tunnelröhre stoßen, müssen wir das Magnetfeld vergrößern.
Sehr praktisch sind dafür die angebrachten Elektromagneten. Diese können sehr unterschiedliche Magnetfelder erzeugen, je nachdem, welches benötigt wird.
Hier findet also eine erste Synchronisation statt.
Weiterhin müssen auch die elektrisches Felder an die Umlaufgeschwindigkeit angepasst werden.
Diese werden mit einer Wechselspannung betrieben. Daher muss die Frequenz der Wechselspannung an die Kreisfrequenz der Teilchenbewegung angepasst werden.
Da die Geschwindigkeit jedoch nicht konstant ist, sind auch die Umlaufdauer und damit die Kreisfrequenz nicht konstant.
Hier muss auch eine Anpassung stattfinden.
Wie du siehst, finden im Synchrotron mehrere Anpassungen statt. So kann gewährleistet werden, dass auch bei sehr hohen Geschwindigkeiten stets eine konstante Kreisbahn beschrieben werden kann.
An dieser Stelle unterscheiden sich Synchrotron und Zyklotron sehr deutlich. Während ein Teilchen im Zyklotron eine spiralförmige Bahn beschriebt, die von innen nach außen immer größer wird, ist die Bahn im Synchrotron konstant.