Massenspektrometer
Entdecke das Massenspektrometer! Erforsche seinen Aufbau, seine Funktionsweise und Einsatzmöglichkeiten. Lerne, wie es Atome und Moleküle nach ihrer Größe sortiert und dabei auf elektrischen und magnetischen Feldern basiert. Neugierig geworden? Vertiefe dein Wissen in der faszinierenden Welt der Spektrometrie!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Massenspektrometer
Massenspektrometer – einfach erklärt
Den Begriff Spektrometer kennst du vermutlich schon aus dem Physikunterricht. Mit Spektrometern kann man Spektren abbilden und messen. Im Falle von Licht kann das beispielsweise die Lichtintensität in Abhängigkeit von der Wellenlänge sein.
Mit einem Massenspektrometer kann man die Masse von Atomen oder Molekülen bestimmen, indem man sie der Größe nach sortiert.
Das Messprinzip basiert vor allem auf den folgenden Punkten:
- Kraft auf geladene Teilchen (Ionen) im elektrischen Feld
- Kraft auf geladene Teilchen (Ionen) im Magnetfeld
Wir wollen uns im Folgenden anschauen, wie ein Massenspektrometer im Detail funktioniert. Dabei betrachten wir das Massenspektrometer nach Bainbridge. Es gibt auch andere Bauweisen – die Grundidee ist aber immer ähnlich.
Massenspektrometer – Aufbau
Wir schauen uns zunächst an, aus welchen Bestandteilen ein Massenspektrometer aufgebaut ist.
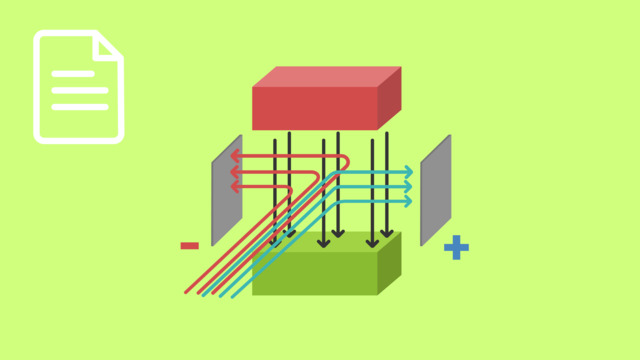
Zunächst werden in einer Ionenquelle die Ionen erzeugt. Es kann sich dabei sowohl um Atome als auch um Moleküle handeln. Eine mögliche Bauform der Ionenquelle sind Atomöfen, in denen ein Material durch starkes Erhitzen verdampft und im Anschluss durch Stöße mit Elektronen ionisiert wird.
Die Ionen werden dann in die erste Kammer beschleunigt, in der Kondensatorplatten ein elektrisches Feld $E$ erzeugen, das senkrecht zu einem Magnetfeld $B$ steht. Nach Durchlaufen der ersten Kammer gelangen sie durch eine kleine Blende in eine zweite Kammer, die ebenfalls von einem Magnetfeld durchsetzt ist. Wir nennen das Magnetfeld in der zweiten Kammer $B^{\prime}$. Hier beschreiben die Ionen eine Kreisbahn und treffen schließlich auf eine Fotoplatte, auf der sie eine geschwärzte Markierung hinterlassen.
Beide Kammern sind evakuiert – in ihnen herrscht also ein Vakuum. Das ist wichtig, da die Ionen andernfalls ständig mit Luft- oder Gasteilchen stoßen und so abgebremst würden.
Wusstest du schon?
Der Nobelpreis für Physik von 1906 ging an J.J. Thomson, der das Elektron mit Hilfe eines frühen Massenspektrometers entdeckte. Dank dieser Entdeckung können wir heute viele verschiedene Substanzen bis auf ihre Atome genau untersuchen!
Massenspektrometer – Funktionsweise
Um die Funktionsweise des Massenspektrometers zu verstehen, vollziehen wir die Bahn eines einzelnen geladenen Teilchens nach.
Massenspektrometer – der Geschwindigkeitsfilter
Wir stellen uns ein Ion mit positiver Ladung $q$ vor, das sich mit einer Geschwindigkeit $v$ durch die erste Kammer bewegt. Innerhalb der Kammer wirken zwei Kräfte auf das geladene Teilchen: Die Kraft im elektrischen Feld $F_{el}$ und die durch das magnetische Feld hervorgerufene Lorentzkraft $F_L$.
Da das Ion positiv geladen ist, zeigt die Kraft $F_{el}$ zur negativ geladenen Platte, also senkrecht zur Bewegungsrichtung nach oben in unserer Abbildung. Die Richtung der Lorentzkraft $F_L$ kann mit der Drei-Finger-Regel der rechten Hand bestimmt werden. Sie zeigt hier senkrecht zur Bewegungsrichtung nach unten. Sie wirkt also der elektrischen Kraft entgegen. Nur wenn beide Kräfte exakt gleich groß sind, heben sie sich gegenseitig auf und das Ion erreicht die zweite Kammer. Sind die Kräfte ungleich, wird es abgelenkt und verfehlt die Blende. Es muss also gelten:
$F_{el} = F_L$
Setzen wir die Formeln für die Kraft im elektrischen Feld und die Lorentzkraft ein, erhalten wir:
$q \cdot E = q \cdot v \cdot B$
Wir können auf beiden Seiten durch die Ladung $q$ und das Magnetfeld $B$ teilen. Dann erhalten wir:
$v = \dfrac{E}{B}$
Damit kennen wir die Geschwindigkeit $v$ der Ionen, die die zweite Kammer erreichen. Über die Größen $E$ und $B$ können wir die dazu passende Geschwindigkeit experimentell sogar beliebig einstellen. Deswegen nennt man diesen Teil des Aufbaus auch einen Geschwindigkeitsfilter.
Massenspektrometer – der Massenfilter
Die Ionen, die die Blende passieren, gelangen in die zweite Kammer. Dort wirkt die Lorentzkraft $F_L^{\prime}$ durch das Magnetfeld $B^{\prime}$ auf sie und zwingt sie auf eine Kreisbahn. Die Lorentzkraft wirkt also als Zentripetalkraft $F_Z$. Die Richtung der Lorentzkraft können wir wieder durch die Drei-Finger-Regel der rechten Hand bestimmen. Den Radius der Kreisbahn können wir berechnen, indem wir die Formeln für Lorentzkraft und Zentripetalkraft gleichsetzen:
$F_L^{\prime} = F_Z $
$q \cdot v \cdot B^{\prime} = \dfrac{m \cdot v^{2} }{r}$
Dabei ist $m$ die Masse des Ions und $r$ der Radius der Kreisbahn. Diese Gleichung können wir nach $m$ umstellen, indem wir mit $r$ multiplizieren und durch $v^{2}$ teilen:
$m = q \cdot B^{\prime} \cdot r \cdot \dfrac{1}{v}$
Wenn wir jetzt noch die oben hergeleitete Gleichung für die Geschwindigkeit $v$ einsetzen, erhalten wir für das Massenspektrometer die Formel:
$m = q \cdot B^{\prime} \cdot r \cdot \dfrac{B}{E}$
In dieser Gleichung sind $B$, $B^{\prime}$ und $E$ Größen, die wir durch das Experiment vorgeben können. Den Radius können wir anhand der Position auf der Fotoplatte ablesen. Nur die Ladung können wir nicht direkt bestimmen. Allerdings muss sie ein ganzzahliges Vielfaches der Elementarladung $e$ sein. Wir sehen anhand der Formel außerdem, dass eine zweifache Ladung im Vergleich zur einfachen Ladung zu einem halbierten Radius führt – also gut unterscheidbar ist.
Massenspektrometer – Anwendungen
Massenspektrometer werden nicht nur in der Physik, sondern auch in vielen anderen Bereichen wie der Chemie, der Geologie oder Archäologie verwendet. Sie werden beispielsweise genutzt, um verschiedene Isotope zu bestimmen.
Fehleralarm
Nicht selten wird angenommen, dass ein Massenspektrometer nur Elemente nachweisen kann. Tatsächlich kann es auch Moleküle und ihre Isotope aufgrund der leicht unterschiedlichen Massen identifizieren.
So kann man auch das Mengenverhältnis von verschiedenen, in einer Probe auftretenden Isotope bestimmen, wenn man deren Massen eindeutig zuordnen kann.
Ausblick – das lernst du nach Massenspektrometer
Erweitere dein Wissen über die Anwendungen von magnetischen Feldern. Themen wie die Magnetschwebebahn oder der Magnetresonanztomograph (MRT) bieten dir spannende Einblicke in die verschiedenen Anwendungsbereiche.
Zusammenfassung
- Das Massenspektrometer ist ein Aufbau zur Bestimmung der Massen von geladenen Teilchen. Das können ionisierte Atome oder Moleküle sein.
- Die Massenbestimmung beruht auf der Ablenkung geladener Teilchen in einem Magnetfeld. Hierbei ist die Lorentzkraft gleich der Zentripetalkraft. Es gilt: $F_{L} = F_{Z}$
- Die Auswahl bestimmter Teilchen wird durch einen Geschwindigkeitsfilter sichergestellt, der die Ablenkung geladener Teilchen in einem elektrischen Feld sowie einem Magnetfeld nutzt. Hierbei ist die Kraft im elektrischen Feld gleich der Lorentzkraft. Es gilt: $F_{el} = F_{L}$
- Durch diese Methode können in einer Probe auftretende Isotope bestimmt werden, sowie deren Mengenverhältnis zueinander, wenn die zugehörigen Massen bereits bekannt sind.
Häufig gestellte Fragen zum Thema Massenspektrometer
Transkript Massenspektrometer
Schönen guten Morgen. Hier ist er wieder, euer Robert Schabloni, heute mit dem Massenspektrometer. Das Massenspektrometer ist ein Gerät, dass man dafür benutzt, um die Masse von Atomen und Molekülen zu bestimmen. Es gibt verschiedene Methoden, wie man das machen kann und wir besprechen hier das Massenspektrometer, nach dem Herrn Bainbridge. Wie funktioniert das? Man benutzt dafür die Kraft im elektrischen Feld auf ein geladenes Teilchen, dann benutzt man die Kraft im magnetischen Feld auf ein bewegtes, geladenes Teilchen, also die Lorentzkraft und man braucht natürlich geladene Teilchen, Ionen, die Atome, wo man die Masse von bestimmen will, muss man also ioniesieren. Hier habe ich jetzt mal ein Massenspektrometer hingezeichnet. Ich habe hier also eine schematische Zeichnung gemacht und das will ich jetzt erst mal erklären, was das alles für Sachen sind, die man hier sieht. Das große S, das steht für die Ionenquelle, da werden die Atome jonisiert und sausen dann raus. Die Ionen kann man erzeugen, indem man den Stoff da drin ganz heiß macht und denke mal die Ionen da mit einer Beschleunigungsspannung hinaussaugen. Hier haben wir dann einen Plattenkondensator, mit einem elektrischen Feld, senkrecht zu dem elektrischen Feld ist ein magnetisches Feld angelegt, hier durch die blauen Punkte dargestellt. Wenn die Ionen es nun also dadurch geschafft haben, dann gelangen sie in einen Bereich, wo also nur ein magnetisches Feld ist, das B-Strich hier, und da bewegen sie sich dann in einer Kreisbahn und treffen dann auf eine Wand, auf eine Fotoplatte. Rot gestrichelt ist hier die Flugbahn der Teilchen. Ja, also dieser Kreis hat einen Radius, diese Kreisbahn, und ich zeichne jetzt hier mal in Grün den Durchmesser ein von dieser Kreisbahn 2r, 2 mal den Radius. Hier unten auf der Fotoplatte kann man dann anhand des schwarzen Fleckes erkennen wo die Ionen aufgetroffen sind. Extrem wichtig bei der ganzen Sache ist, dass im Inneren dieses Apparates ein Vakuum herrschen muss. Ansonsten können die Ionen da gar nicht durchfliegen, sie würden von der Luft gebremst. Wir betrachten jetzt mal die Vorgänge im Inneren des Massenspektrometers genauer. Wir haben hier also einen Plattenkondensator gehabt und der ist also von einem Magnetfeld durchsetzt gewesen. Das sind die blauen Punkte. Die elektrischen Feldlinien zeichne ich jetzt mal wegen der Übersichtlichkeit nicht ein, aber ihr wisst natürlich, dass sie von Plus nach Minus laufen. Das Ganze ist nun also so angeordnet, dass das elektrische Feld und das Magnetfeld senkrecht aufeinander stehen. So, und jetzt fliegen wir mal von links ein geladenes Teilchen rein, hier in Rot gezeichnet. Das hat eine positive Ladung. Es wird also zur negativen Kondensatorplatte hinabgelenkt. Hervorgerufen durch die Kraft q×E. In die entgegengesetzte Richtung wirkt dann die Lorentz-Kraft und die können wir schreiben als q×v×B. Wenn die beiden Kräfte betragsmäßig gleich sind, dann heben sie sich auf und das Teilchen wird überhaupt nicht abgelenkt, es fliegt gerade durch. Ich schreib das also mal hier rechts als Gleichung hin: q×E=q×v×B Das heißt also, die elektrische Anziehungskraft ist gleich der Lorentzkraft. FE=FL. Wenn man also das elektrische Feld und das magnetische Feld eingestellt hat, dann hängt das also von der Geschwindigkeit ab, ob das Teilchen dann durchkommt oder es abgelenkt wird. Deswegen sagt man dazu auch : Geschwindigkeitsfilter. Wir wollen jetzt die Geschwindigkeit ausrechnen, die das Teilchen haben muss, um grade durchzufliegen. Aus der Gleichung können wir das q herauskürzen, und dann noch einmal durch B teilen und die gesuchte Geschwindigkeit ist dann gerade E:B. Teichen, die also gerade diese Geschwindigkeit haben, werden nicht abgelenkt, sondern fliegen gerade durch den Filter hindurch. Dann gelangen sie in den nächsten Teil des Massenspektrometers, wo sich nur ein Magnetfeld befindet. Ja, wie ihr sicherlich wisst, führt das zu einer Kreisbahn die die Ionen dann beschreiten. Das liegt daran, dass die Lorentzkraft gerade die Zentripetalkraft liefert, die für die Kreisbahn gebraucht wird. FZ ist die Zentripetalkraft und die ist gleich der Lorentzkraft FL. Die Lorentzkraft hatten wir heute schon einmal q×v×B und die Zentripetalkraft, die schreibt sich m×vquadrat:r. Und an das B mache ich jetzt noch einen Strich, damit wir dieses Magnetfeld von dem anderen Magnetfeld, von dem Geschwindigkeitsfilter unterscheiden können. Jetzt kürze ich mal ein v aus dieser Gleichung raus, dann multipliziere ich mit r, dann teile ich noch einmal durch v und dann haben wir das Ganze umgestellt nach der Masse. m ist jetzt=q×BStrich×r×1:v v war =E:B und der Kehrwert davon, 1:v ist dann B:E Als Ergebnis können wir also festhalten dass m=q×r×B×BStrich:E ist. Von dieser Formel können wir eigentlich alle Größen, die wir zur Bestimmung von m brauchen, messen. das r kann man ja am Detektor, an der Photoplatte ablesen, aber das q, die Ladung von dem Jon, die kann man nun leider nicht so direkt messen. Allerdings haben die meisten Ionen, die man in der Jonquelle erzeugt, eine Elementarladung, also q=e. Wenn die jetzt eine größere Ladung haben, also q ist zum Beispiel 2e, dann fliegen die auf einer engeren Kreisbahn mit dem halben Radius. Das kann man auch an der Formel sehen, wenn man q verdoppelt und r halbiert, dann bleibt m gleich. Diese Auftreffpunkte liegen also weit auseinander, man wird sich da nicht so leicht vertun. Man kann mit dem Massenspektrometer auch feststellen, dass Elemente aus verschiedenen Isotopen zusammengesetzt sind. Diese Isotope, also Atome, wo sich die Masse geringfügig unterscheidet und die zu einem Element gehören, die treffen also dicht nebeneinander auf. So, jetzt sind wir also schon fast am Ende, aber eine Sache möchte ich noch klären. Wenn ihr eine Klausur schreibt und ihr sollt da ein Massenspektrometer skizzieren, dann müsst ihr natürlich auch wissen, wie man die Richtung von v, von B und von E richtig wählt. Wenn man ein Magnetfeld zeichnet und dafür Punkte hinmalt, dann heißt das, dass die Magnetfeldlinien aus der Zeichenebene herauszeigen, also nach oben. Nun soll von rechts ein positiv geladenes Teilchen in das Magnetfeld hineinfliegen. Die Richtung der Lorentzkraft, die kann man nur bestimmen mit der Drei-Finger-Regel, der rechten Hand. Für negativ geladene Teilchen kann man das mit der Drei-Finger-Regel der linken Hand machen. Wir nehmen also den Daumen und halten ihn in die Bewegungsrichtung des geladenen Teilchens. Den Zeigefinger halten wir in Richtung der Magnetfeldlinien und dann halten wir den Mittelfinger senkrecht zu den beiden anderen Fingern, und das ist dann die Richtung der Lorentzkraft. Wenn wir nun einen Geschwindigkeitsfilter bauen wollen, müssen wir also die negativ geladene Kondensatorplatte oben hinmachen und unten die positiv geladene. Denn nur so kann die elektrische Ablenkungskraft q×E, die Lorentzkraft kompensieren. Wenn man das Magnetfeld mit so Kreuzen zeichnet, dann heißt das, das zeigt nach unten, also in die Zeichenebene hinein. So, und nun soll ein Teilchen von rechts nach links fliegen. Es ist ebenfalls wieder positiv geladen. Also, wir halten jetzt den Daumen nach links und den Zeigefinger nach unten und dann spreizen wir den Mittelfinger ab und jetzt zeigt der nach gerade hier, also da nach unten an die Bildschirmkante. Nun müssen wir also den Plattenkondensator genauso bauen, wie eben auch, also mit der negativen Kondensatorplatte oben hin und die positiv geladene unten hin, damit das Teilchen da andersherum abgelenkt wird, also nach oben. Jetzt wisst ihr also, worauf man achten muss, wenn man ein Geschwindigkeitsfilter zeichnet. Ja und das war es dann auch zum Massenspektrometer. Ich verabschiede mich. Bis zum nächsten Mal.
Massenspektrometer Übung
-
Gib an, welche Aussagen über das Massenspektrometer zutreffen.
TippsDas Massenspektrometer besteht unter anderem aus einem Geschwindigkeitsfilter.
Nach dem Geschwindigkeitsfilter findet sich ein evakuiertes Vakuumrohr.
LösungDas Massenspektrometer beruht auf einigen wenigen physikalischen Grundannahmen.
Zunächst müssen die betrachteten Teilchen unbedingt elektrisch geladen sein. Es kommen daher Elektronen, Protonen oder Ionen als Probekörper infrage. Neutronen oder nach außen elektrisch neutrale Elemente oder Moleküle können nicht verwendet werden. Das liegt daran, dass auf die Teilchen die Lorentzkraft wirken soll, um eine Kreisbewegung zu erzeugen und so anhand des Radius eine Aussage über die Masse machen zu können. Es wirkt also eine Kraft im Magnetfeld.
Aufgrund dieser Kraft werden die geladenen Teilchen auf eine Kreisbahn bewegt und letztendlich auf eine Photoplatte geschossen. Je nach Auftreffpunkt kann man nun bestimmen, wie schwer das auftreffende Teilchen sein musste.
Wichtig ist dabei, dass im Inneren des Massenspektrometers ein Vakuum herrscht. Andernfalls treffen die beschleunigten Ionen, schon bevor sie auf die Photoplatte treffen, auf Gasmolekühle, sodass keine Messung mehr möglich wäre.
-
Bezeichne den Aufbau des Massenspektrometers.
TippsUnter Einwirkung der Lorentzkraft verlaufen die Ionen auf einer Kreisbahn.
Die Lorentzkraft wirkt auf bewegte Ladungsträger.
Den Kondensator mit angelegtem Magnetfeld können nur Ionen mit bestimmter Geschwindigkeit passieren.
Die Messung muss im Vakuum stattfinden.
LösungDas Massenspektrometer besteht im Wesentlichen aus vier Bauteilen, die innerhalb eines evakuierten Raumes angebracht sind.
Das erste Bauteil ist eine Ionenquelle. Diese erzeugt freie Ionen, indem etwa eine Heizspule unter Spannung gesetzt wird. Diese freien, geladenen Teichen werden beschleunigt und durch einen Geschwindigkeitsfilter gelenkt. Dieser Filter ist das zweite Bauteil. Diesen können nur Ionen bestimmter Geschwindigkeit passieren. Aufgrund des elektrischen Feldes werden zu langsame Ionen zu den Platten des Kondensators abgelenkt. Ionen, die zu schnell sind, werden aufgrund der Lorentzkraft ausgesiebt.
Die Ionen, welche den Filter passieren, gelangen durch eine Blende in den zweiten Teil des Massenspektrometers. Hier sind die Ionen wieder einem magnetischen Feld ausgesetzt, sozusagen dem dritten Bauteil des Messgerätes. Auch hier wirkt die Lorentzkraft und die Ionen werden auf eine Kreisbahn gelenkt. Der Radius der Kreisbahn ist dabei äquivalent zur Masse der Ionen. Auf einer Photoplatte, dem vierten Bauteil, werden die Ionen detektiert. So kann der Radius der Kreisbewegung genau ermittelt und schlussendlich mit dem Ansatz $m = \frac{q \cdot B' \cdot r}{v} $ bestimmt werden.
Die Messung muss dabei im Vakuum stattfinden. Andernfalls würden die Ionen mit den Gasmolekülen stoßen und ihre Bewegungsenergie verlieren. Eine zuverlässige Messung wäre nicht weiter möglich.
-
Berechne die Geschwindigkeit der Ionen hinter dem Geschwindigkeitsfilter.
TippsRechne in den Grundeinheiten.
Es soll $ F_E = F_L$ sein.
Es gilt $ q \cdot E = q \cdot v \cdot B$.
LösungIn einem Geschwindigkeitsfilter steht ein Magnetfeld der Stärke $B$ senkrecht auf dem elektrischen Feld $E$ eines Kondensators.
Bringt man nun eine beschleunigte Ladung senkrecht zu $B$ und $E$ in den Geschwindigkeitsfilter ein, so wirken auf den Probekörper zum einen die Kraft $ F_E = q \cdot E $ aus der elektrischen Anziehung des elektrischen Feldes sowie die Lorentzkraft $ F_L = q \cdot v \cdot B$.
Nur, wenn sich die beiden Kräfte im Gleichgewicht befinden, kann ein Teilchen den Filter passieren.
Setzen wir also $ F_E = F_L$. Damit ist $ q \cdot E = q \cdot v \cdot B$. Nun kürzen wir das $q$ weg und erhalten : $ E = v \cdot B $. Umgestellt nach $v$ ergibt sich nun $ v = \frac{E}{B} $.
Die Filterwirkung hängt also nur von der Stärke des elektrischen Feldes und der Magnetfeldstärke ab.
Für einen Filter mit : $ E =1,45~\frac{\text{kV}}{\text{m}} $ und $B = 278~\text{mT}$ ergibt sich $ v = \frac{E}{B} = \frac{1{,}45~\frac{\text{kV}}{\text{m}}}{278~\text{mT}} = \frac{1450~\frac{\text{V}}{\text{m}}}{0{,}278~\text{T}} =5\,215{,}83~\frac{\text{m}}{\text{s}}$.
Achte bei der Berechnung unbedingt darauf, in den Grundeinheiten zu rechnen.
-
Berechne die Massen.
Tipps$ v = \frac{E}{B} $
Rechne in den Grundeinheiten.
$m = \frac{q \cdot r \cdot B' \cdot B}{E}$
LösungUm die Masse eines Teilchens zu berechnen, welches auf die Photoplatte des Massenspektrometers aufgetroffen ist, müssen wir zunächst einmal dessen Ladung und Geschwindigkeit kennen. Zudem müssen wir das an der Vakuumröhre angelegte Magnetfeld kennen sowie den Radius der Kreisbewegung.
Sind diese Größen bekannt, so können wir die Formel $m = \frac{q \cdot r \cdot B' \cdot B}{E}$ anwenden.
Doch wo finden wir hier die Geschwindigkeit? Im Massenspektrometer ist ein sogenannter Geschwindigkeitsfilter integriert. Dieser besteht aus einem Kondensator, auf den ein ausgerichtetes Magnetfeld wirkt. Tritt nun ein geladenes Teilchen hindurch, wird dieses entweder vom magnetischen oder elektrischen Feld abgelenkt oder diese beiden Wirkungen heben sich auf und das Teilchen passiert den Filter. So kann sichergestellt werden, dass nur Teilchen mit einer bestimmten Geschwindigkeit in die Vakuumröhre des Massenspektrometers eintreten. Es gilt der Zusammenhang $v = \frac{E}{B}$.
Die Teilchen, die den Geschwindigkeitsfilter passiert haben, sind nun also alle gleich schnell und werden in die Vakuumröhre eingeleitet. Hier werden sie nun durch das Magnetfeld $B'$ ausgerichtet. Dieses ist nicht gleich dem Magnetfeld im Geschwindigkeitsfilter. Als Folge der Lorentzkraft werden die geladenen Teilchen auf eine Kreisbahn gelenkt und treffen auf einer Photoplatte auf. Anhand des Auftreffpunkts kann nun der Radius der Kreisbewegung $r$ abgemessen werden. Nun kann man alle Größen einsetzen und erhält als Ergebnis die Masse des untersuchten Teilchens.
Betrachten wir ein Beispiel: Ein Ion mit doppelter Einheitsladung $e$ tritt einen Geschwindigkeitsfilter mit $E = 1{,}1~\frac{\text{kV}}{\text{m}}$ und $B = 5~\text{mT}$. In der anschließenden Vakuumröhre herrscht ein Magnetfeld von $B' = 32{,}2~\text{T}$. Der Radius der Kreisbahn wird zu $ r = 7{,}7~\text{mm}$ bestimmt.
Wir setzen in $m = \frac{q \cdot r \cdot B' \cdot B}{E}$ ein und erhalten so $m = \frac{3{,}2 \cdot 10^{-19} \cdot 0{,}0077~\text{mm} \cdot 32{,}2~\text{T} \cdot 0{,}005~\text{T}}{1\,100~\frac{\text{V}}{\text{m}}}$.
Als Ergebnis erhalten wir nun $m = 3{,}61 \cdot 10^{-25}~\text{kg}$.
-
Gib die Funktion des Massenspektrometers an.
TippsEs wirkt die Lorentzkraft.
Die Lorentzkraft wirkt auf bewegte Ladungsträger.
LösungDas Massenspektrometer ist, wie der Name schon vermuten lässt, ein Messgerät zur Bestimmung der Masse von Atomen und Molekülen.
Mit Hilfe eines Geschwindigkeitsfilters werden nur Ionen, die sich mit einer bestimmen Geschwindigkeit bewegen, in eine Vakuumröhre geleitet. Hier sind sie nun ausschließlich einem magnetischen Feld ausgesetzt und werden aufgrund der Lorentzkraft auf eine Kreisbahn gelenkt. Diese Kraft wirkt ausschließlich auf geladene Teilchen. Neutronen oder neutrale Teilchen werden also nicht beeinflusst und sind daher auch nicht messbar. Je nachdem, wie stark das Magnetfeld, wie groß die Masse des Ions und wie schnell dieses ist, trifft es an einer bestimmten Stelle auf einer Photoplatte auf. Man kann über den Radius der Kreisbewegung bestimmen, welche Masse das Ion haben muss.
So können auch die Massen sehr leichter Teilchen bestimmt werden.
-
Bestimme die fehlenden Begriffe.
TippsIsotope sind meist nur wenige Neutronenmassen leichter oder schwerer als ihre elementaren Atome.
Der Radius der Ionenbewegung verhält sich proportional zur Ionenmasse.
Im Geschwindigkeitsfilter gilt : $v = \frac{E}{B}$.
LösungUm die Aussagen zu überprüfen, betrachten wir zunächst den Geschwindigkeitsfilter. Nur Ionen mit einer bestimmten Geschwindigkeit können diesen passieren. Mit dem Ansatz <nobr>$v = \frac{E}{B}$</nobr> kann die Durchtrittsgeschwindigkeit ermittelt werden. Für den Fall, das $E$ und $B$ den gleichen Betrag aufweisen, ergibt sich dann mit <nobr>$E = B$</nobr> in <nobr>$v = \frac{E}{B} = \frac{E}{E} = 1~\frac{\text{m}}{\text{s}}$.</nobr> Für einen Geschwindigkeitsfilter mit <nobr>$E = 3{,}9~\frac{\text{kv}}{\text{m}}$</nobr> und <nobr>$B = 1{,}1~\text{T}$</nobr> ergibt sich aus dem gleichen Ansatz <nobr>$v = \frac{3,9~\frac{\text{kv}}{\text{m}}}{1{,}1~\text{T}} = 3\,545{,}45~\frac{\text{m}}{\text{s}}$.</nobr>
Da die Masse eines Teilchens direkt proportional zum Radius der Ionenbahn ist, treffen schwere Teilchen weiter außen auf als leichtere. Das ist damit zu erklären, dass der Radius der Ionenbahn zunimmt und der Abstand zwischen Blende und Auftreffpunkt ebenfalls steigt.
Haben Teilchen ähnliche Massen, wie es bei den Isotopen einer Atomart der Fall ist, treffen diese logischerweise nah beieinander auf der Photoplatte auf. Auch hier liegt die Proportionalität von Radius und Masse zugrunde. Isotope sind ja nur ein wenig leichter oder schwerer als ihre elementaren Ionen, denn der Gewichtsunterschied besteht meist in wenigen Neutronenmassen.
Du siehst: Mit einigen simplen Ansätzen lassen sich auch relativ komplexe Fragestellungen zum Massenspektrometer leicht beantworten.
8.883
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.852
Lernvideos
37.617
Übungen
33.734
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Wie entsteht Ebbe und Flut?
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohm'Sches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt
Ich denke das es eine Verbesserung wäre, wenn die Rechnung der Testfrage, wie z.B. bei diesem Video, am Ende, nach der Antwort eingeblendet werden würde.
So hätte man dann die Möglichkeit es zumindest nachzuvollziehen, und kann eventuell noch offene Fragen erkennen und diese dann unter dem Video zu klären. Ich beende nun dieses Video mit dem Makel die Aufgabe nicht gelöst zu haben. :-(
Ein Lob an den Sprecher. Hahahaha. :)
hallo :)) ich habe eine frage und zwar : wenn an wolkenlosen sommertagen die sonne zehn stunden lang scheint , dann ist insgesamt eine energie von 18MJ pro Quadrat meter eingestrahlt worden. um wie viel erhöht sich dadurch die temperatur im schwimmbecken ( Wassertiefe 2,5m) und im Planschbecken ( wassertiefe 0,8 m)?
@Patrick: Du hast recht. Bei der ersten Erklärung des Geschwindigkeitsfilters zeigt die Lorentzkraft in die falsche Richtung und damit Lorentzkraft und elektrische Kraft in entgegengesetze Richtungen zeigen müsste mann plus und minus beim Plattenkondensator vertauschen.
Du hast einen kleinen Fehler gemacht! Wie du am Ende richtig beschreibst muss die obere Platte im Geschwindigkeitsfilter negativ geladen sein. Fehler: Bei 3:47 muss es sich aber um ein negatives Teilchen handeln wenn die Lorentzkraft nach oben wirken soll. Wenn es aber negativ ist, wird es nicht von der unteren negativ geladenen Platte angezogen.
Gruß Patrick