Zyklotron


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Zyklotron
In diesem Video wird das Zyklotron vorgestellt, eine frühe Art des Kreisbeschleunigers. Ein Zyklotron besteht aus zwei halbkreisförmigen, durch einen schmalen Spalt getrennten Duanten, die senkrecht von einem Magnetfeld durchsetzt sind. Das Magnetfeld hält die zu beschleunigenden Teilchen im Duant auf einer halbkreisförmigen Bahn. Durch Wahl einer Wechselspannung mit geeigneter Frequenz werden die Teilchen bei jedem Durchgang durch den Spalt beschleunigt, wobei sich ihr Bahnradius stetig vergrößert. Zum Schluss werden noch die Formeln, die zur Berechnung einer Beschleunigung im Zyklotron notwendig sind, hergeleitet.
Transkript Zyklotron
Hallo und herzlich willkommen zu Physik mit Kalle. Wir wollen uns heute aus dem Gebiet Elektrizität und Magnetismus mit dem Zyklotron beschäftigen. Wir lernen heute, was ein Zyklotron ist, wie es aufgebaut ist und was in ihm passiert und zum Schluss wollen wir uns die Formeln ansehen, mit deren Hilfe man die Bahn geladener Teilchen in einem Zyklotron berechnen kann. Dann wollen wir mal. Ein Zyklotron ist eine etwas ältere Form eines Kreisbeschleunigers, in dem geladene Teilchen wiederholt beschleunigt und dabei von einem Magnetfeld auf einer Spiralbahn gehalten werden. Erfunden wurde das Ganze 1929 von Ernest Lawrence, den ihr hier mit seinem Kollegen Lewingston vor dem 1. Zyklotron seht. Ihr könnt die beiden dicken Magnetpole oben und unten sehen. Was aber nun wirklich genau im Zyklotron passiert, das wollen wir uns nun im nächsten Kapitel ansehen. Obwohl es inzwischen deutlich bessere Teilchenbeschleuniger gibt, wird das Zyklotron, weil es so einfach zu bauen ist, auch heute noch eingesetzt. Vor allem für medizinische Zwecke, wie z.B. Strahlentherapie. Ein Zyklotron besteht aus 2 Duanten, die senkrecht von einem Magnetfeld durchsetzt sind. Im Englischen sagt man wegen der Form einfach Di, stellt euch das Ganze am besten vor wie eine runde Sardinenbüchse die einfach in der Mitte durchgeschnitten ist. In der Mitte unseres Zyklotron befindet sich eine Ionenquelle, die also geladene Teilchen ausspuckt. Zwischen den Duanten. die durch einen schmalen Spalt getrennt sind, liegt die hochfrequente Wechselspannung UB an, mit deren Hilfe geladene Teilchen im Spalt beschleunigt werden. Hat UB die richtige Frequenz, dann werden die Teilchen mit jedem Durchgang durch den Zwischenraum beschleunigt. In dem Duanten wirkt nur das magnetische Feld. Daher beschreiben die Teilchen dort Halbkreisbare. Durch die wiederholte Beschleunigung wächst der Radius der Halbkreisbahnen beständig und daher folgt das Teilchen insgesamt einer Spiralbahn, bis es auf den Auslass trifft und das Zyklotron verlässt. Wie diese Spiralbahn nun genau aussieht und vor allem wie sie zustande kommt, das wollen wir uns nun im nächsten Kapitel ansehen. Durch die wiederholte Beschleunigung wächst der Radius der Halbkreisbahnen beständig und daher folgt das Teilchen insgesamt einer Spiralbahn, bis es auf den Auslass trifft und das Zyklotron verlässt.2 Sardinenbüchsenhälften, getrennt durch einen Spalt, der hier auf dem Bild deutlich größer ist, als in Wirklichkeit, und das Ganze wird durchsetzt von einem Magnetfeld. Zwischen diesen beiden Büchsenhälften schließen wir die Wechselspannung UB an. So, fast fertig. Jetzt fehlt uns nur noch die Ionenquelle im Spalt und dann kann es losgehen. Unser Ion wird nun von der Beschleunigungsspannung beschleunigt. In welche Richtung? Das hängt davon ab, wie sie gerade gepolt ist. Wir sagen mal, es geht nach links. Betritt unser Teilchen nun den Duanten, wirkt nur noch eine Kraft, und zwar die Lorenzkraft. Sie wirkt senkrecht zu Bewegungsrichtung und zur Magnetfeldrichtung. In unserm Fall, für ein positiv geladenes Teilchen, also nach unten. Falls ihr euch nun beschwert warum die Lorenzkraft auch mit im Beschleunigungsspalt wirkt, ihr habt ja recht, das tut sie, aber wie ich vorhin schon gesagt habe, in Wirklichkeit ist der Beschleunigungsspalt winzig. D.h. die Lorenzkraft innerhalb des Spaltes kann vernachlässigt werden. Zurück zu unserem Teilchen. Es wirkt also die Lorenzkraft Q×v×B. Und da sich weder Q noch V noch B im Duanten ändern, fliegt unser Teilchen also auf einer Kreisbahn. Die Bahn des Teilchens ist also ein Halbkreis, bis es wieder im Beschleunigungsspalt ankommt. Und in der Zwischenzeit soll sich unsere Beschleunigungsspannung umgepolt haben, sodass unser Teilchen diesmal nach rechts beschleunigt wird. Wie unsere Halbkreisbahn nun aussehen wird, nachdem wir das zweite Mal den Beschleunigungsspalt durchquert haben, das können wir einfach herausfinden, indem wir folgenden Ansatz machen. Die Lorenzkraft hält unser Teilchen auf der Kreisbahn, sie ist also die Zentripetalkraft. Darum können wir schreiben mv2/r=Q×v×B. Lös ich das auf nach dem Radius, dann erhalte ich: r=m×V/Q×B. Da meine Geschwindigkeit V nun mit jedem Durchgang durch den Beschleunigungsspalt steigen soll, ist auch der Radius meiner Halbkreisbahn nach jedem Durchlauf durch den Beschleunigungsspalt größer. Unser Teilchen beschreibt also wieder eine Halbkreisbahn, mit größerem Radius und kommt zum 2mal am Beschleunigungsspalt an. Die Polung der Beschleunigungsspannung sollte sich wieder geändert haben, sodass es erneut durch den Spalt beschleunigt wird. Dadurch steigt erneut der Radius der Kreisbahn im Duanten. Und so soll das Ganze immer weiter gehen. Ihr seht, der Trick bei der ganzen Geschichte ist, dass die Beschleunigungsspannung immer richtig gepolt ist, um unser Teilchen zu beschleunigen. Dazu muss ich die Umlaufdauer meines Teilchens herausfinden, um die Frequenz meiner Wechselspannung darauf abzustimmen. Darum kümmern wir uns aber im letzten Kapitel. Zuerst wollen wir uns noch ein anderes Problem ansehen. Wie ihr vielleicht gemerkt habt, wächst der Radius eines Teilchens mit jedem Durchlauf durch den Beschleunigungsspalt langsamer. Das könnte natürlich daran liegen, dass ich kein besonders guter Zeichner bin und das ist normalerweise auch kein schlechter Tipp. Diesmal ist es allerdings Absicht. Wie wir herausgefunden hatten, hängt der Radius von Masse, Geschwindigkeit, Ladung und Magnetfeld ab. Da M, Q, B konstant sein sollen, wollen wir mal sehen, ob wir nicht einen Ausdruck für die Geschwindigkeit finden. Wir setzen dazu die aufgewertete Beschleunigungsarbeit Wel gleich der gewonnenen kinetischen Energie, Wkin. Das ergibt für n-Durchläufe die Formel: Q×n×UB=½×mvn2. Lös ich das nach vn auf, dann erhalte ich, die Geschwindigkeit vn nach dem n-ten Durchlauf durch den Beschleunigungsspalt ist die \sqrt(2×Q×b×UB)/m. Ihr seht also, da wie vorhin schon gesagt, Q, UB und m konstant sind, wächst die Geschwindigkeit vn mit der Wurzel der Anzahl der Umläufe. Also vn ist proportional zu \sqrtn. Die Geschwindigkeit läuft also umso langsamer, je mehr Umläufe ich schon hinter mir habe. Und genau das Gleiche, ihr könnt es in der Formel oben sehen, gilt damit auch für den Radius. Wir können uns also merken: Die Zunahme des Bahnradius wird nach außen immer kleiner. Wie nun das Problem mit der Umlaufdauer gelöst wird, das wollen wir uns im letzten Kapitel ansehen. Mit welchen Formeln man diese Bewegungen berechnen kann, das können wir uns im letzten Kapitel ansehen. Dann wollen wir doch mal sehen, was ich hier für Ansätze machen kann. Als 1., für die Beschleunigung des geladenen Teilchens, die elektrische Energie, die zur Beschleunigung des Teilchens aufgewendet wird, ist gleich der kinetischen Energie. Ich kann also schreiben: n×Q×U für n-Beschleunigungen =½×m×vn2. Für die Halbkreisbahn kann ich schreiben: Die Kraft, die meine geladenen Teilchen auf ihrer Bahn hält, ist die Lorenzkraft. Ich schreibe also die Zentripetalkraft ist die Lorenzkraft oder m×v2/r=Q×v×B. Da ich hier gleich ein wenig umformen muss, mach ich mir erst mal eine kleine Skizze und ein paar Notizen. Ihr erinnert euch vielleicht, die Geschwindigkeit eines Objekts das sich auf einem Kreis bewegt, ist gleich dem Radius × der Winkelgeschwindigkeit. Ich schreibe also: v=ω×r. Wobei ω die Winkelgeschwindigkeit ist. Damit ist die Umlaufdauer T=2×π/ω. Und wenn ich diese beiden Gleichungen benutze, kann ich schreiben: 2×π×r/T=ω×r=v. Das macht auch Sinn. Bei der Geschwindigkeit v brauche ich für 2×π×r, was ja genau der Umfang des Kreises ist, exakt die Umlaufdauer T. So, damit bewaffnet machen wir uns nun mal auf die Suche nach der Formel für die Umlaufdauer T des Zyklotrons. Wir benutzen unseren Ansatz für die Halbkreisbahn, aus dem wir 1 v kürzen können und schreiben: m×vn/r=Q×B. Dies will ich nun umformen. Ihr seht, link steht v/r, wenn ich meine v=ω×r Formel nach ω auflöse, erhalte ich ω=v/r. Ich kann also links, statt v/r auch ω einsetzen. Wenn ich nun die Formel für meine Umlaufdauer nach ω auflöse, erhalte ich ω=2π/T. Ich kann also auch gleich statt v/r, 2π/T einsetzen. Damit erhalte ich also m×2π/T=Q×B oder aufgelöst nach der Umlaufdauer: T=2πm/Q×B. Ihr seht also, solange sich die Masse, die Ladung und die Magnetfeldstärke nicht ändern, ist die Umlaufdauer für alle Geschwindigkeiten gleich. Das ist ein wunderschönes Ergebnis für unser Problem. Solange ich also m, Q und B kenne, kann ich die Umlaufdauer der Teilchen für alle Geschwindigkeiten ausrechnen. Sie ist konstant und damit kann ich einfach mit Frequenz=1/Umlaufdauer, die Frequenz meiner Wechselspannung nun so einstellen, dass die Teilchen mit jedem Durchgang durch den Spalt beschleunigt werden. Probleme bekomme ich erst, wenn meine Teilchen so schnell werden, dass ich die relativistische Massenzunahme berücksichtigen muss. D.h. sobald ich relativistische Geschwindigkeitszunahmen erreiche, muss ich meine Formel anpassen. Denn dann steigt die Masse ja mit der Geschwindigkeit. Wir merken uns: Wenn ich relativistisch rechne, muss ich statt der Masse die relativistische Masse m=die Ruhemasse m0/\sqrt(1-v2/c2) einsetzen. Man muss relativistisch rechnen, sobald die Geschwindigkeit v des Teilchens 1/10 der Lichtgeschwindigkeit erreicht hat. Deswegen ist das Zyklotron übrigens für Elektronen eher ungeeignet. Aufgrund ihrer geringen Masse, werden sie im Spalt stark beschleunigt und erreichen damit viel zu schnell relativistische Geschwindigkeiten. Wir wollen noch mal wiederholen, was wir heute gelernt haben: Ein Zyklotron ist ein früher Kreisbeschleuniger, der aber auch heute noch wegen seiner Einfachheit, vor allem für medizinische Zwecke eingesetzt wird. Er besteht aus 2 Duanten, die sich in einem Magnetfeld befinden und zwischen denen eine hochfrequente Wechselspannung anliegt. Die Umlaufdauer ist für nicht-relativistische Geschwindigkeiten T=2πm/QB. Ist v größer oder gleich 1/10 der Lichtgeschwindigkeit, so muss ich relativistisch rechnen. Dann muss ich für die Masse m die Ruhemasse m0/\sqrt(1-v2/c2) einsetzen. So das wars schon wieder für heute. Ich hoffe, ich konnte euch helfen. Vielen Dank fürs Zuschauen. Vielleicht bis zum nächsten Mal, euer Kalle.
Zyklotron Übung
-
Definiere, was ein Zyklotron ist.
TippsDie Bahn der Teilchen verändert sich mit jedem Umlauf im Zyklotron.
Es liegt eine Ionenquelle in der Mitte des Zyklotrons vor.
Die Bewegung entsteht durch die Lorentz-Kraft.
LösungDas „Zyklotron" ist ein Kreisbeschleuniger, in dem Ionen wiederholt beschleunigt und durch ein Magnetfeld auf einer spiralen Bahn gehalten werden.
Dass Zyklotron besteht aus den zwei „Duanten", an welche eine Wechselspannung angelegt wird. Zusätzlich sind die beiden Duanten von einem Magnetfeld durchsetzt. In der Mitte des Zyklotrons, zwischen den Duanten, befindet sich eine Ionenquelle. Hier kommen die geladenen Teilchen her.
Es liegt hier also ein Magnetfeld und ein Strom (bewegte Ladung) vor. Als Resultat wirkt eine Kraft: die Lorentzkraft. Von dieser Kraft beschleunigt bewegen sich die Teilchen von der Ionenquelle ausgehend auf immer größer werdenden Kreisbahnen spiralförmig nach außen. So entsteht ein gerichteter Ionenstrahl, der zum Beispiel für medizinische Zwecke (Strahlentherapie) Anwendung findet.
-
Bestimme die zutreffenden Aussagen.
Tipps$ f = \frac {1}{T} $
Liegt die Spannung in der falschen Frequenz vor, bremst die Lorentzkraft, anstatt zu beschleunigen.
$ v_{n} = \sqrt{\frac{2 \cdot Q \cdot n \cdot U_B}{m}} $
LösungIm Zyklotron finden wir eine Vielzahl von physikalischen Einflussgrößen. Zum einen müssen wir den Aufbau des Zyklotrons beachten, zum anderen die Eigenschaften der anliegenden Spannung und der beschleunigten eingebrachten Ionen. Das verhält sich so wie bei einem Katapult. Hier müssen wir ebenfalls die Eigenschaften des Wurfgeschosses (Masse, Luftwiderstand) und die Geometrie des Katapultes (Höhe, Schwungmasse) betrachten, um eine Vorhersage über Wurfweite und kinetische Energie machen zu können.
Fangen wir mit der Umlaufdauer an : Diese gehorcht der Formel $ T = \frac{2 \cdot \pi \cdot m }{Q B} $. Also ist $ T $ eine Funktion von Masse $m$ , Ladung $Q$ und Magnetfeld $B$.
Damit eine Beschleunigung der Ionen überhaupt stattfinden kann, muss die Umlaufdauer an die Frequenz der Wechselspannung angepasst werden. Sonst würde die Lorentzkraft in die falsche Richtung wirken und die Ionen ausbremsen. Die Frequenz $ f $ der Wechselspannung folgt dabei der Formel $ f = \frac {1}{T} $. Diese muss dem Kehrwert der Umlaufdauer entsprechen.
Durch den Ansatz $ W_{el} = W_{kin} $ erhalten wir die Formel zur Berechnung der Geschwindigkeit der beschleunigten Ionen : $ v_{n} = \sqrt{\frac{2 \cdot Q \cdot n \cdot U_B}{m}} $ . Hier siehst du, dass die Geschwindigkeit $v$ mit der Wurzel der Umläufe steigt. Sie nimmt also mit jedem Umlauf im Zyklotron immer weiter zu, aber um immer geringer werdende Beträge. Die Größen $m$,$Q$ und $U_B$ sind hier konstant.
Erreicht die Geschwindigkeit ein Zehntel der Lichtgeschwindigkeit, so treten relativistische Effekte auf, die wir berücksichtigen müssen. Dazu nutzen wir die Formel $ m = \frac{m_0}{\sqrt{1-\frac{v^2}{c}}} $, wobei $m_0$ die Ausgangsmasse des betrachteten Teilchens ist, $c$ die Lichtgeschwindigkeit und $v$ die momentane Geschwindigkeit.
-
Bewerte die Aussagen.
Tipps$ F_Z = F_L $
$ r = \frac{m \cdot v^2}{Q \cdot v \cdot B}$
$ T = \frac{2 \pi r}{\omega r v } $
LösungUm die Bahn eines Teilchens um die Ionenquelle des Zyklotrons zu beschreiben, bedienen wir uns eines einfachen Ansatzes :
$ F_Z = F_L $.
Die Lorentzkraft soll also genau der Zentripetalkraft entsprechen.
Umgeformt nach dem Radius $r$ erhalten wir:
$ r = \frac{m \cdot v^2}{Q \cdot v \cdot B}$.
Der Radius ist also abhängig von Masse $m$ , Bahngeschwindigkeit $v$, Ladung $Q$ und Magnetfeld $B$.
Hier sehen wir bereits, dass der Radius **direkt proportional zu $m$ und $v$ und umgekehrt proportional zu $ Q$ und B$ ist.
Die Umlaufdauer stellen wir mit $ T = \frac{2 \pi r}{\omega r v } $ dar. ( mit $ f = \frac{1}{T}$ folgt also $ f = \frac{\omega r v }{2 \pi r} $ )
Hier siehst du, dass die Umlaufdauer $T$ umgekehrt proportional von der Winkel- $\omega$ und der Bahngeschwindigkeit $v$ abhängt. (Umgekehrt gilt dieser Zusammenhang für $f$ )
-
Berechne die anzulegende Frequenz der Wechselspannung.
TippsDie Lorentzkraft muss in Bewegungsrichtung wirken.
Frequenz und Umlaufdauer stehen in einem wohldefinierten Verhältnis.
$ f =\frac {1}{T} $
LösungFrequenz und Schwingung stehen in einem festdefinierten Verhältnis: Die Frequenz entspricht genau dem Kehrwert der Umlaufdauer $ f = \frac{1}{T} $. Damit die Umlaufdauer des beschleunigten Ions mit der Polung der Wechselspannung übereinstimmt, muss also die Frequenz angepasst sein. (Der Grund dafür ist, dass die Lorentzkraft immer in Beschleunigungsrichtung wirken muss, damit das Ion nicht gebremst wird.)
Wir müssen also die Richtung der Lorentzkraft auf die Bewegungsrichtung der Teilchen abstimmen. (Die Richtung der Lorentzkraft hängt ja von der Richtung des Stromes ab, also der Polung der Spannung.)
Wie bereits erklärt, funktioniert das mithilfe der Frequenz der Wechselspannung.
Ein Beispiel :
** Die Umlaufdauer betrage $ T = 0,01s $. Bilden wir den Kehrwert, ergibt sich nach $ f =\frac {1}{T} = \frac{1}{0,01s} = 100 s^{-1} = 100 Hz $. Die passende Frequenz beträgt hier 100 Hertz. **
-
Benenne den Entwickler des Zyklotrons.
TippsDer Erfinder ist ein US-Amerikaner.
Er wirkte an der Entwicklung der Atombombe mit.
Das 103. Element des Periodensystems ist nach ihm benannt.
LösungDer Erfinder des Zyklotrons ist der US-amerikanische Atomphysiker Ernest Lawrence. Er erhielt für die Entwicklung des Zyklotrons und die damit erzielten Ergebnisse im Jahre 1939 den Physik-Nobelpreis.
Außerdem wurde das Element Lawrencium, welches an Stelle 103 des Periodensystems zu finden ist, nach ihm benannt.
Er arbeitete maßgeblich an der Erfindung der ersten Atombombe während des Zweiten Weltkriegs mit.
Heute wird das Zyklotron weniger für die Erzeugung künstlicher Elemente verwendet (man hat mittlerweile bessere Technik dafür entwickelt), dafür umso mehr in der Medizin bei der Strahlentherapie.
-
Errechne die relativistische Masse.
Tipps$c = 299792458 \frac{m}{s} $
Relativistische Effekte treten erst auf, wenn ein Teilchen auf eine Geschwindigkeit von $v_t = 0,1 \cdot c $ beschleunigt wurde.
LösungDie relativistische Masse errechnet sich nach der Formel $ m_{rel} = \frac{m_0}{ \sqrt {1- \frac{v^2}{c}}}$ . Darin ist $m_0$ die Masse des ruhenden Teilchens, $v2$ die Geschwindigkeit des beschleunigten Teilchen und $c$ die Lichtgeschwindigkeit mit $c = 299792458 \frac{m}{s} $.
Ganz wichtig ist es, die Massen in $kg$ und die Geschwindigkeiten in $ \frac{m}{s} $ anzugeben. Sonst entstehen Rechenfehler aufgrund der falschen Einheiten.
Relativistische Effekte treten erst auf, wenn ein Teilchen auf eine Geschwindigkeit von $v_t = 0,1 \cdot c $ beschleunigt wurde. Bei kleineren Geschwindigkeiten sind diese Effekte sehr klein.
Mit diesen Angaben zur relativistischen Masse konntest du Albert hoffentlich weiterhelfen !
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.314
Lernvideos
38.636
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?







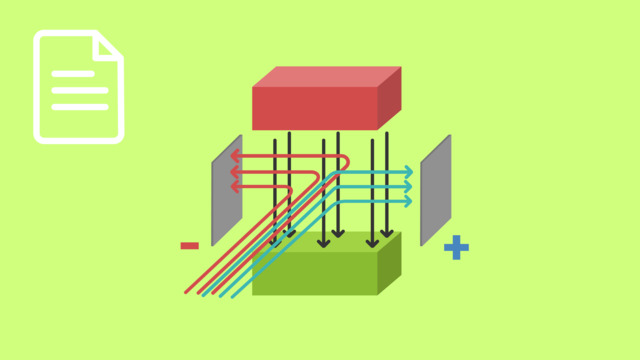










Diese Formel gehört zum elektrischen Feld, sie bestimmt die Beschleunigung der Ladungen im elektrischen Feld.
Für den einmaligen Durchlauf beträgt die Beschleunigungsarbeit wie gewohnt: W_el = Q * U_B
Also Ladung Q mal Beschleunigungsspannung U_B.
Da beim Zyklotron jedoch viele Durchläufe erfolgen, wird diese mit der Anzahl der Durchläufe n multipliziert.
Wir erhalten die Formel: W_el = n * Q * U_B.
woher hat man denn für Wel die Formel W*n*Ub (minute 5:54)
Super Video !
Allerdings habe ich eine Frage. Im Video kommen folgende Ansätze vor : Wel = Wkin und Eel = Ekin
Wo liegt da der unterschied ?
Seh ich genauso sehr verständlich
sehr sehr gutes Video :D