Magnetisches Feld
Stromdurchflossener Leiter; Magnetische Feldstärke; Lorentzkraft;Magnetfeld in einer langen Spule; Materie im magnetischen Feld; Magnetische Flussdichte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Magnete
Du kennst bereits Permanentmagnete und hast vielleicht auch schon einen Elektromagneten gesehen. Diese Magnete sind in der Lage, Körper aus ferromagnetischen Materialien über eine gewisse Entfernung anzuziehen.
Doch wie sind Elektromagnete aufgebaut? Du weißt du bereits, dass Magnete zwei Pole besitzen: den Nord- und den Südpol. Ebenso weißt du schon, dass sich gleichnamige Pole abstoßen und ungleichnamige Pole anziehen.
Aus dem Eisenspan-Experiment konntest du sehen, dass sich Eisenspäne anhand von Feldlinien orientieren und ausrichten.
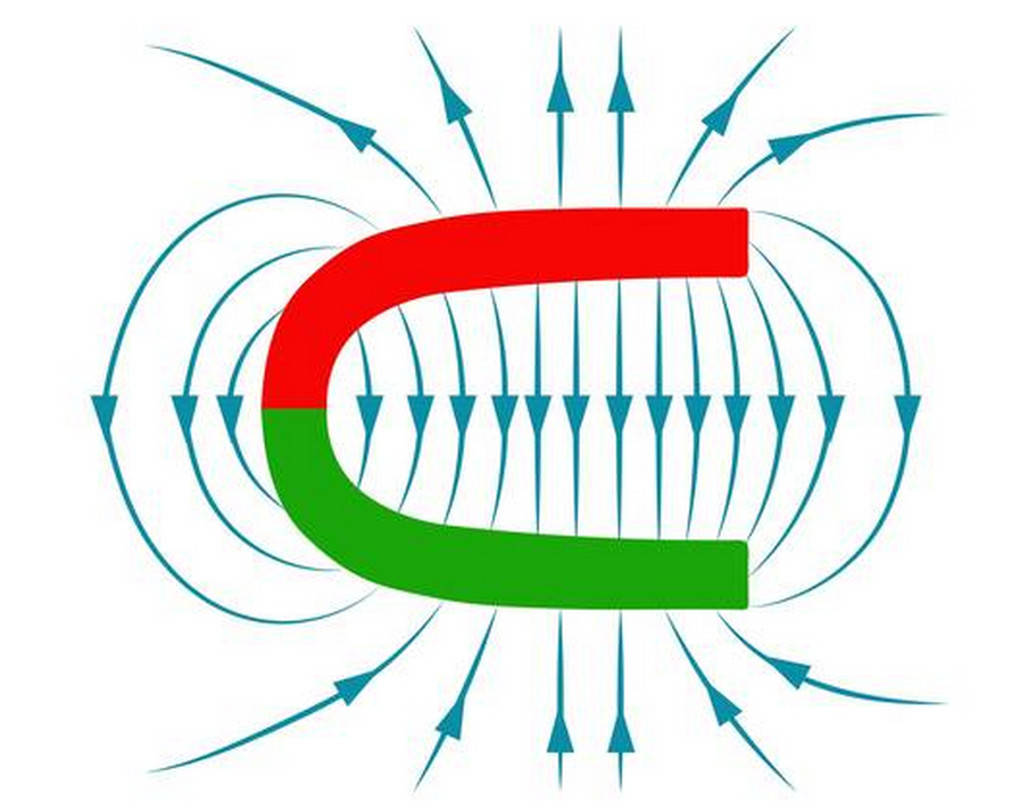
Diese Feldlinien bilden in ihrer Gesamtheit das magnetische Feld. Die magnetischen Feldlinien haben laut Definition eine eindeutige Richtung: Sie verlaufen von Nord nach Süd. Zudem schneiden sich diese Feldlinien nie. Nach diesen Regeln können wir das magnetische Feld leicht zeichnen.
Größen des magnetischen Feldes
Zur Beschreibung des magnetischen Feldes unterscheidet man drei häufig vermischte physikalische Größen: die magnetische Feldstärke $H$, die magnetische Flussdichte $B$ und den magnetischen Fluss $\Phi$.
Die magnetische Feldstärke gibt an, wie stark das Magnetfeld in einem bestimmten Abstand zur Quelle ist. Sie lässt sich beim Elektromagneten über die elektrische Stromstärke des verursachenden Stroms bestimmen.
$H=\frac{\text{Stromstärke }I}{2 \pi\cdot\text{Abstand zum Leiter }d},~[H]=1\frac Am$
Die magnetische Flussdichte gibt an, wie groß die Flächendichte des magnetischen Feldes ist, welche senkrecht durch eine definierte Fläche tritt. Die Einheit der magnetischen Flussdichte ist das Tesla.
$B=\frac{\text{Kraft auf den Leiter im Magnetfeld }F}{\text{Stromstärke }I\text{ Länge des Leiters }l},~[B]=1T =1\frac{V\cdot s}{m^2}=1\frac{Wb}{A}$
Der magnetische Fluss beschreibt wiederum die Stärke des magnetischen Stroms im Magnetfeld analog zur elektrischen Stromstärke in einem Leiter. Er hat die Einheit Weber.
$\Phi=B\cdot A,~[\Phi]=1Wb=1 V\cdot s= 1 T \cdot m^2$
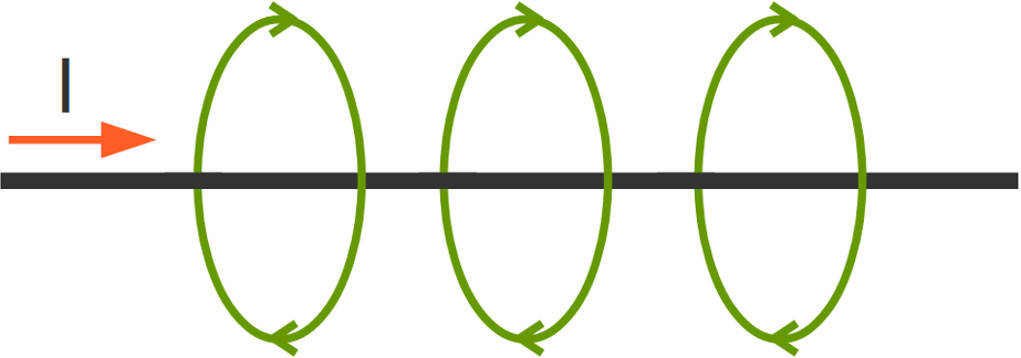
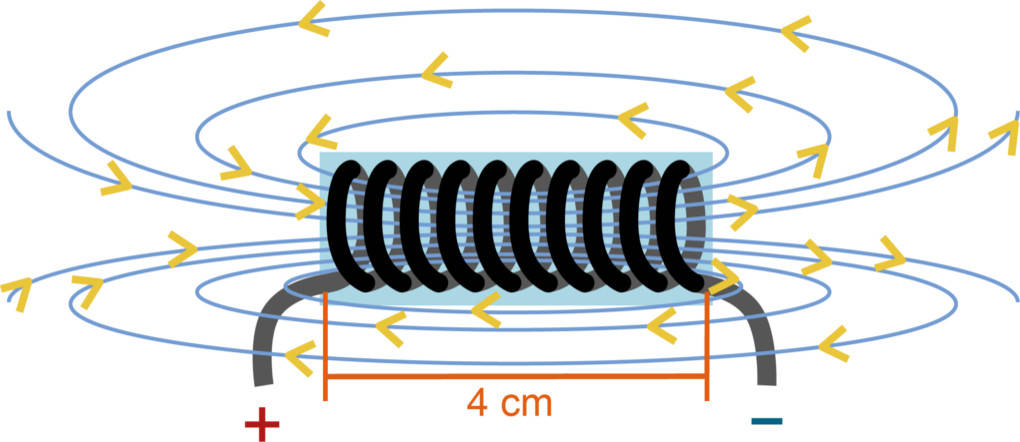
Magnetfelder von unterschiedlichen Leitern!
Für den geraden stromdurchflossenen Leiter gelten die oben genannten Formeln. Die Formel für den magnetischen Fluss ist sogar universell gültig. Es gibt jedoch Unterschiede, sobald man den Leiter zu einer Spule wickelt. Hier ist die Windungszahl $N$ wichtig und $l$ beschreibt nicht mehr die Länge des Leiters, sondern die Länge der Spule.
$H=\frac{N \cdot I}{l}$
$B=\mu_r \cdot \mu_0\cdot\frac{N\cdot I}{l}$
Dabei ist $\mu_0$ die magnetische Feldkonstante und $\mu_r$ die relative Permeabilität. Letztere unterscheidet sich je nach Medium, welches sich innerhalb der Spule befindet und kann Formelsammlungen entnommen werden.
Lorentzkraft
Im magnetischen Feld wirkt eine Kraft auf alle bewegten Ladungsträger und stromdurchflossenen Leiter: die Lorentzkraft. Diese Kraft ist direkt von der magnetischen Flussdichte und der Stromstärke abhängig.
Sie ist bei einem kleinen Elektromagneten noch relativ schwach, ein Magnetresonanztomograph (MRT) muss, obwohl er eher schwer ist, am Boden befestigt werden, um nicht wegen des starken elektrischen Stroms und des sehr starken magnetischen Feldes der Lorentzkraft zu folgen. Dass sich der MRT bewegen möchte, können wir am lauten Knacken im MRT wahrnehmen.
Die Lorentzkraft lässt sich für einen geraden, stromdurchflossenen Leiter über folgende Formel bestimmen.
$F_L=l\cdot I \cdot B$
Für eine Spule geht die Windungzahl $N$ zusätzlich als Faktor ein und $l$ entspricht wieder der Länge der Spule.
$F_L=N \cdot l\cdot I \cdot B$
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Magnetisches Feld (11 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Magnetisches Feld (11 Arbeitsblätter)
-
 Kräfte im Magnetfeld
PDF anzeigen
Kräfte im Magnetfeld
PDF anzeigen -
 Magnetfeld eines geraden, stromdurchflossenen Drahtes
PDF anzeigen
Magnetfeld eines geraden, stromdurchflossenen Drahtes
PDF anzeigen -
 Magnetfeld von Spulen
PDF anzeigen
Magnetfeld von Spulen
PDF anzeigen -
 Magnetische Permeabilität µ
PDF anzeigen
Magnetische Permeabilität µ
PDF anzeigen -
 Lorentzkraft – Kraft auf bewegte Ladungsträger im Magnetfeld
PDF anzeigen
Lorentzkraft – Kraft auf bewegte Ladungsträger im Magnetfeld
PDF anzeigen -
 Lorentzkraft – bewegte Ladung und Ströme im magnetischen Feld
PDF anzeigen
Lorentzkraft – bewegte Ladung und Ströme im magnetischen Feld
PDF anzeigen -
 Magnetischer Fluss Φ und magnetische Flussdichte B – Vergleich
PDF anzeigen
Magnetischer Fluss Φ und magnetische Flussdichte B – Vergleich
PDF anzeigen -
 Energie einer stromdurchflossenen Spule
PDF anzeigen
Energie einer stromdurchflossenen Spule
PDF anzeigen -
 Energiedichte von Feldern
PDF anzeigen
Energiedichte von Feldern
PDF anzeigen -
 Bestimmung der spezifische Ladung am Fadenstrahlrohr
PDF anzeigen
Bestimmung der spezifische Ladung am Fadenstrahlrohr
PDF anzeigen -
 Felder im Vergleich
PDF anzeigen
Felder im Vergleich
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie























