Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule
Erfahre, wie man mithilfe eines Fadenstrahlrohrs die spezifische Ladung eines Elektrons misst und somit seine Masse bestimmen kann. Entdecke, wie die Lorentzkraft Elektronen auf Kreisbahnen zwingt und erhalte Einblicke in den experimentellen Aufbau. Interesse geweckt? Das und mehr im folgenden Text!


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule
Die Bestimmung der spezifischen Ladung eines Elektrons mit dem Fadenstrahlrohr
Wir wollen uns im Folgenden damit beschäftigen, wie man mithilfe eines Fadenstrahlrohrs die spezifische Ladung eines Elektrons bestimmen kann und weshalb diese Größe von Bedeutung ist. Dazu schauen wir uns zunächst an, was die spezifische Ladung überhaupt ist und wie ein Fadenstrahlrohr aufgebaut ist.
Die spezifische Ladung
In der Physik bezeichnet man das Verhältnis von Ladung $Q$ zu Masse $m$ eines Körpers als seine spezifische Ladung. Sie gibt also an, wie viel Ladung ein Körper pro Masseeinheit hat. Die Einheit der spezifischen Ladung ist daher Coulomb pro Kilogramm beziehungsweise Amperesekunde pro Kilogramm:
$ \left[ \frac{Q}{m} \right] = \frac{ \text{C} }{ \text{kg} } = \frac{ \text{As} }{ \text{kg} } $
Wenn man die spezifische Ladung und die Ladung eines Körpers kennt, kann man so seine Masse bestimmen. Im Falle des Elektrons kennen wir seine Ladung bereits aus dem Millikan-Versuch. Wenn wir die spezifische Ladung messen, können wir so die Masse des Elektrons bestimmen.
Das Fadenstrahlrohr
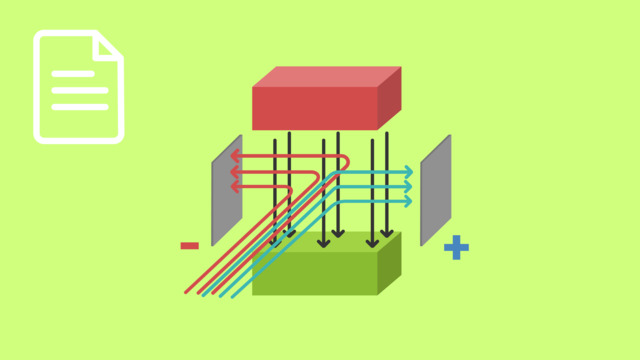
Das Fadenstrahlrohr ist ein experimenteller Aufbau, in dem die Wirkung der Lorentzkraft auf bewegte Ladungen in Magnetfeldern ausgenutzt wird, um die spezifische Ladung zu ermitteln. Das Experiment ist folgendermaßen aufgebaut:
Der Glaskolben ist bei sehr niedrigem Druck von einigen $10^{-6}~\text{bar}$ mit einem Edelgas wie beispielsweise Argon gefüllt. Der Glaskolben befindet sich in einer Helmholtzspule. Als Helmholtzspule bezeichnet man eine spezielle Anordnung von zwei großen, von Gleichstrom durchflossenen Spulen. Sie sind derart angeordnet, dass sich zwischen den einzelnen Spulen ein annähernd homogenes Magnetfeld ausbildet. Innerhalb des Kolbens befindet sich außerdem eine Elektronenkanone. Durch eine Heizspannung $U_H$ werden hier Elektronen aus einem Heizdraht ausgelöst und anschließend durch die Beschleunigungsspannung $U_B$ beschleunigt.
Wie funktioniert das Fadenstrahlrohr?
Nachdem die Elektronen mit der Ladung $q$ durch die Beschleunigungsspannung $U_B$ beschleunigt wurden, haben sie eine Geschwindigkeit $v$, die mit der kinetischen Energie $E_{kin} = qU_B$ zusammenhängt. Mit dieser Geschwindigkeit bewegen sie sich senkrecht zu dem von der Helmholtzspule erzeugten Magnetfeld $B$. Dadurch wirkt auf die Elektronen die Lorentzkraft
Jetzt können wir eine Formel aufstellen, um die spezifische Ladung des Elektrons zu bestimmen. Wir haben schon festgestellt, dass sich die Elektronen durch die Lorentzkraft $F_L$ auf einer Kreisbahn bewegen. Das bedeutet, dass die Lorentzkraft als Zentripetalkraft $F_Z$ wirkt. Es gilt also:
$F_L = F_Z$
Setzen wir die bekannten Formeln für die Lorentz- und die Zentripetalkraft ein, erhalten wir:
$q \cdot v \cdot B = m_e \cdot \frac{v^{2}}{r}$
Darin ist $m_e$ die Masse des Elektrons, $v$ seine Geschwindigkeit und $r$ der Radius der Kreisbahn. Das Verhältnis aus $q$ und $m_e$ wollen wir bestimmen, $B$ und $r$ können wir messen. Wir brauchen also noch eine Formel für die Geschwindigkeit $v$, die wir nicht direkt messen können. Wir hatten schon gesagt, dass sie mit der kinetischen Energie zusammenhängt, die die Elektronen durch die Beschleunigungsspannung $U_B$ erhalten, also:
$E_{kin} = qU_B$
Darin können wir die Formel für die kinetische Energie ausschreiben:
$\frac{1}{2} \cdot m_e \cdot v^{2} = q \cdot U_B$
Diesen Ausdruck müssen wir noch nach $v^{2}$ umstellen und anschließend die Wurzel ziehen. So erhalten wir:
$v = \sqrt{ \frac{ 2 \cdot q \cdot U_B }{ m_e } }$
Das können wir nun in die erste Gleichung einsetzen. Vorher quadrieren wir diese allerdings, damit wir keine Wurzelterme mehr betrachten müssen:
$q^{2} \cdot v^{2} \cdot B^{2} = m_e^{2} \cdot \frac{v^{4}}{r^{2}}$
Jetzt setzen wir für $v$ ein:
$q^{2} \cdot \frac{ 2 \cdot q \cdot U_B }{ m_e } \cdot B^{2} = m_e^{2} \cdot \frac{ \left( \frac{ 2 \cdot q \cdot U_B }{ m_e } \right)^{2} }{r^{2}}$
Diesen Ausdruck können wir noch vereinfachen. Zunächst können wir auf beiden Seiten durch $\frac{ 2 \cdot q \cdot U_B }{ m_e } $ teilen, anschließend können wir auf beiden Seiten durch $q$ teilen und auf der rechten Seite $m_e^{2}$ mit $m_e$ kürzen. So erhalten wir:
$q \cdot B^{2} = \frac{m_e}{r^{2}} \cdot 2 \cdot U_B$
Jetzt teilen wir auf beiden Seiten durch $m_e$ und $B^{2}$ und erhalten als endgültige Formel:
$\frac{q}{m_e} = \frac{2\cdot U_B}{B^{2} \cdot r^{2}}$
Alle Größen der rechten Seite können wir experimentell bestimmen und damit die spezifische Ladung $q/m_e$ des Elektrons berechnen.
Die aktuell genauesten Messungen ergeben den folgenden Wert:
$\frac{q}{m_e} \approx -1,759 \cdot 10^{11}~\frac{\text{C}}{\text{kg}} = \frac{-e}{m_e}$
Die Ladung des Elektrons ist $-e$, wobei $e$ die positive Elementarladung ist. Da wir den Wert der Ladung des Elektrons bereits aus dem Millikan-Versuch kennen, können wir mithilfe dieser Formel die Masse des Elektrons bestimmen. Dazu formen wir zunächst um, indem wir mit $m_e$ multiplizieren und durch die spezifische Ladung teilen und erhalten:
$m_e \approx \frac{e}{1,759 \cdot 10^{11}~\frac{\text{C}}{\text{kg}}}$
Dann setzen wir den Wert für die Elementarladung, $e = 1,602 \cdot 10^{-19}~\text{C}$, ein und erhalten für die Masse des Elektrons:
$m_e = 9,1 \cdot 10^{-31}~\text{kg}$
Transkript Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule
Hallo und herzlich willkommen bei Physik mit Kalle! Wir wollen uns heute aus dem Gebiet Elektrizität und Magnetismus mit der spezifischen Ladung des Elektrons beschäftigen und wie man sie mit einem Helmholtzspulenpaar und einer Fadenstrahlröhre bestimmen kann. Wir lernen heute, was die spezifische Ladung ist und warum sie uns überhaupt interessiert, welchen Versuchsaufbau wir benutzen, um sie zu ermitteln, und welche Geräte dabei verwendet werden und wie man dann genau aus den Versuchsergebnissen die Elektronenmasse berechnen kann. Dann wollen wir mal. Die spezifische Ladung gibt an, wie viel Ladung ein Körper im Verhältnis zu seiner Masse hat. Ihre Einheit ist damit C/kg (Coulomb pro kg) oder A×s/kg (Amperesekunde pro kg). Die spezifische Ladung interessiert uns aus folgendem Grund: Kennt man die spezifische Ladung Q/m eines Körpers und seine Ladung Q, so kann man seine Masse berechnen. Da man die Elektronenladung bereits aus dem Millikan-Versuch kennt, ist die Ermittlung der spezifischen Ladung (und damit der Elektronenmasse) mit dem Fadenstrahlrohr und einem Helmholtzspulenpaar ein beliebter Schulversuch. Und wie der genau funktioniert, wollen wir uns im nächsten Kapitel ansehen. Links im Bild seht ihr den fertigen Versuchsaufbau. Der Glaskolben in der Mitte ist das Fadenstrahlrohr. Ein Fadenstrahlrohr ist ein gasgefüllter Kolben, in dem sich eine Elektronenkanone befindet, also eine Elektronenquelle und eine kleine Vorrichtung zum Beschleunigen dieser Elektronen. Das Fadenstrahlrohr befindet sich in der Mitte eines Helmholtzspulenpaares. Ein Helmholtzspulenpaar ist eine spezielle Anordnung aus 2 kurzen Spulen, zwischen denen sich ein nahezu homogenes Magnetfeld bildet. Links im Bild seht ihr eine Skizze des Versuchsaufbaus, mit deren Hilfe wir jetzt kurz den Ablauf des Experiments durchgehen wollen. In der Elektronenkanone werden durch eine Heizspannung UH Elektronen freigesetzt und dann durch eine Beschleunigungsspannung UB beschleunigt. Durch das vom Helmholtzspulenpaar erzeugte Magnetfeld werden sie innerhalb unseres Fadenstrahlrohrs auf einer Kreisbahn gehalten. Dabei stoßen sie die Gasatome an und regen sie so zum Leuchten an. Ihre Flugbahn wird dadurch sichtbar und man kann den Radius der Kreisbahn einfach am Fadenstrahlrohr ablesen. Wir merken uns: Wir kennen den Radius der Kreisbahn r, wir kennen die Beschleunigungsspannung UB der Elektronenkanone und mithilfe der Stromstärke I, mit der wir das Helmholtzspulenpaar betreiben, können wir uns auch die magnetische Flussdichte ausrechnen. Im letzten Kapitel wollen wir uns jetzt ansehen, wie wir, damit bewaffnet, die spezifische Ladung des Elektrons ausrechnen können. Da unsere Elektronen vom Magnetfeld auf der Kreisbahn gehalten werden, können wir wieder den einfachen Ansatz, die Zentripetalkraft (FL) = die Lorentzkraft (FL) machen. Wir schreiben also: Q×v×B=mv2/r. Die Geschwindigkeit der Elektronen müssen wir uns allerdings erst aus der Beschleunigungsspannung herrechnen. Dazu schreiben wir: ½mv2=Q×UB. Oder, umgestellt nach v2: v2=((Q×UB)/m)×2 (Ladung × Beschleunigungsspannung / Masse × 2). Die Geschwindigkeit ist also v=\sqrt((2×Q×UB)/m). Wenn ich nun meinen ersten Ansatz erst kürze und dann ebenfalls nach v umstelle, erhalte ich: Die Geschwindigkeit v=((Q×B)/m)×r. Nun kann ich die beiden Ausdrücke für v gleichsetzen (um die Wurzel loszuwerden, quadriere ich sie gleich beide), und kann schreiben: (Q2×B2×r2/m²=(2×Q×UB)/m. Ich teile zur Vereinfachung durch die Ladung und nehme mit der Masse × (/Q×m). Dann erhalte ich: 2UB=(Q×B2×r2)/m. Und da Q/m ja meine spezifische Ladung ist, muss ich nur noch den ganzen Rest auf die andere Seite bringen und ich habe den Ausdruck, den ich gesucht habe. Q/m= (2UB)/B2×r2 (2 x die Beschleunigungsspannung / magnetische Flussdichte2 × Radius2). Und da ich das alles habe, kann ich es einsetzen und ich erhalte: =1,759×1011C/kg. Aus dem Millikan-Versuch wissen wir: Die Ladung des Elektrons ist die Elementarladung (e) und sie beträgt 1,6×10^-19C. Damit ist die Ladung des Elektrons die Ladung (Q) / die spezifische Ladung (Q/m), also (1,6×10^-19)/(1,759×1011)kg. Und das ergibt für die Elektronenmasse 9,1×10^-31kg. Wir wollen noch einmal wiederholen, was wir heute gelernt haben: Die spezifische Ladung gibt an, wie viel Ladung ein Körper im Verhältnis zu seiner Masse hat. Mithilfe des Fadenstrahlrohrs und eines Helmholtzspulenpaars kann die spezifische Ladung des Elektrons bestimmt werden, um dann (bei bekannter Elementarladung) die Elektronenmasse zu berechnen. Die spezifische Ladung des Elektrons beträgt 1,759×1011C/kg. Und damit kann man die Elektronenmasse zu 9,1×10^-31kg berechnen. So, das war es schon wieder für heute. Ich hoffe, ich konnte euch helfen. Vielen Dank fürs Zuschauen, vielleicht bis zum nächsten Mal, Euer Kalle
Spezifische Ladung des Elektrons – Ermittlung mit Fadenstrahlrohr und Helmholtzspule Übung
-
Gib die Definition der spezifischen Ladung an.
TippsDie spezifische Darstellung hat das Ziel, die Vergleichbarkeit zweier Proben unabhängig von der Masse zu gewährleisten.
Die spezifische Ladung muss direkt proportional zur absoluten Ladung sein.
LösungDie spezifische Ladung ist die auf eine Masse-Einheit festgelegte Ladung.
$ \frac{\text{Ladung}}{\text{Masse}} $
Dabei ist die spezifische Ladung umso größer, je mehr Ladung auf einer geringeren Masse angebracht werden kann.
Sinn und Zweck einer spezifischen Darstellung ist es, unterschiedliche Größenordnungen vergleichbar zu machen.
Anhand der spezifischen Ladung können wir ablesen, wie viel Ladung bezogen auf ein $kg$ von einem Stoff getragen werden kann, unabhängig davon, wie groß oder klein die untersuchte Probe ist.
-
Gib an, was ein Fadenstrahlrohr und Helmholtzspule sind.
TippsVerwendet man nur eine Helmholtzspule ist das erzeugte Magnetfeld nicht homogen.
Fadenstrahlrohr-Versuch = Fadenstrahlrohr + Helmholtzspulenpaar
Eine Elektronenkanone beschleunigt freie Elektronen.
LösungDas Fadenstrahlrohr ist ein mit Gas gefülltes Glasrohr.
In dieses werden durch eine Beschleunigungsspannung $U_B$ beschleunigte freie Elektronen eingebracht.
Man nennt das auch Elektronenkanone.
Bei Stößen mit den Gasmolekülen erzeugen die Elektronen eine sichtbare Leuchtspur.
Helmholtzspulen werden immer paarweise verwendet. (Würden wir nur eine verwendenden, wäre das erzeugte Magnetfeld nicht homogen.)
Indem man diese genau aufeinander ausrichtet, kann man ein nahezu homogenes Magnetfeld erzeugen. Bringt man ein Helmholtzspulenpaar an dem gefüllten Glasrohr an, so ist der Fadenstrahlversuch komplett.
Durch die Einwirkung des homogenen Magnetfeldes, kann man beobachten, dass die bewegten Elektronen auf eine Kreisbahn gebracht und gehalten werden. Das liegt an der Wirkung der Lorentz-Kraft, welche als Resultat aus Magnetfeld und bewegter Ladung resultiert.
Mit dem Fadenstrahlrohrversuch kann die spezifische Ladung des Elektrons ermittelt werden.
-
Erkläre, woher die freien Elektronen beim Fadenstrahlversuch kommen.
TippsElektronen sind in der Regel Bestandteil der Atomhülle.
Um Elektronen aus der Atomhülle zu lösen, ist Energie notwendig.
Es wird hier thermische Energie hinzugefügt.
LösungDamit der Fadenstrahlrohrversuch überhaupt ablaufen kann, müssen freie Elektronen vorhanden sein.
Doch in der Natur kommen diese meist gebunden als Bestandteile der Atomhülle vor. Diese werden dabei von der positiven Ladung der Protonen in unmittelbarer Nähe des Atomkern gehalten, sind also nicht frei.
Um diese Elektronen aus der Hülle zu lösen, wird eine Trennungsenergie benötigt.
Am einfachsten kann man diese als Wärme hinzufügen. Mit einer Heizspannung $ U_H$ wird ein Stoff stark erhitzt, sodass die Elektronen genug Energie erhalten, um der Anziehungskraft des Atomkerns zu trotzen und nun als freie Elektronen vorhanden sind. (Man könnte auch einen hohen Druck erzeugen oder die Atome mit sehr energetischer Strahlung beschießen, was jedoch schwieriger und gefährlicher ist.)
Durch eine Beschleunigungsspannung $U_B$ werden die nun freien Elektronen beschleunigt und in den Glaskolben hineinbewegt.
-
Errechne den Radius der Kreisbahn.
Tipps$r$ nimmt ab, wenn $B$ größer wird.
$r$ nimmt zu, wenn $v$ größer wird.
Rechne immer in den Grundeinheiten.
LösungDer Radius der Bahn, die ein Elektron im Fadenstrahlversuch beschreibt, hängt ab von den Masse $m$ und Elementarladung $e$ , die für ein Elektron ja beide bekannt und konstant sind. Die veränderlichen Größen sind das Magnetfeld $B$ und die Geschwindigkeit der Elektronen $v$.
Wichtig ist, bei Berechnung des Radius $r$ nur die Grundeinheiten zu verwenden, also etwa $[\text{m}]$ statt $[\text{cm}]$ für Längen oder $[\text{s}]$ anstatt $[\text{h}]$ für Zeiträume.
Du kannst beobachten, dass die Bahn der Elektronen bei steigendem Magnetfeld kleiner wird und bei zunehmender Geschwindigkeit der Elektronen ansteigt.
-
Gib an, wie man die Masse aus der spezifischen Ladung ermitteln kann.
TippsDie Ladung und die Masse sind direkt proportional zueinander .
Betrachte die Einheiten.
LösungDie Masse entspricht der Ladung, geteilt durch die spezifische Ladung.
Einen Beweis erhält man mit der Betrachtung der Einheiten:
$ kg = \frac{Q}{\frac{Q}{kg}} = kg $.
Je größer etwa die Ladung eines Körpers ist, desto größer muss auch seine Masse sein.
Stell dir vor, ein Material kann nur ein Elektron pro $kg$ Masse tragen, seine spezifische Ladung wäre also $ \frac{1e^-}{kg} $. Um eine Ladung von 5 Elektronen speichern zu können, müsste man also : $ m_5 = \frac {5e^-}{ \frac{1e^-}{kg}} = 5 kg $ des Stoffes haben.
Die Ladung und die Masse sind also direkt proportional zueinander und über die spezifische Ladung quantitativ miteinander verbunden.
-
Berechne die Masse des Protons.
TippsMasse und Ladung sind proportional zueinander.
Berechnung analog zur Berechnung der Elektronenmasse.
Die Grundladung eines Protons ist genauso groß wie die eines Elektrons.
LösungDie Masse des Proton ergibt sich durch die gleiche Berechnung, die wir auch für die Masse des Elektrons durchführen.
Indem wir die Ladung durch die spezifische Ladung teilen, erhalten wir die Masse $m_p$.
Es gilt :
$m_p = \frac{Ladung}{spezifische Ladung} = \frac{e_p}{\frac{e}{m_p}} = \frac{1,6 \cdot 10^{-19}}{9,58 \cdot 10^4} = m_p = 1,67 \cdot 10^{-24} kg = 1,67 \cdot 10^{-21} g $.
So erhalten wir für die Masse des Proton bei Kenntnis der Elementarladung und der spezifischen Ladung die Masse mit :
$m_p = 1,67 \cdot 10^{-24} kg $.
9.770
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.293
Lernvideos
38.561
Übungen
33.598
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?




















@Ascoras
Die Elektronen als geladene Teilchen, werden in diesem Magnetfeld immer gleich stark, also immer um den gleichen Winkel abgelenkt. Ist das Magnetfeld richtig eingestellt kann man es auf eine perfekte Kreisbahn zwingen.
Aber warum gibt es überhaupt einen KREISFÖRMIGEN elektronenstrahl? Was ist der Grund dafür? ...
sorry, aber wie soll man das verstehen? Wie kommt man auf die ganzen Formeln???
@Paula E.: Die Herleitung der Formel wird in diesem Video gezeigt und erklärt. Alles fängt damit an das man Lorentz- und Zentrifugalkraft gleichsetzt...Viel Spaß beim Anschauen!
Ich mag das Video (:
Kannst du mir verraten wie ich e/m herleite?? Ich kann das mit der formel -
e/m=2*U durch r hoch 2 *B hoch 2 - auch rechnen.
Mein Lehrer hat aber gesagt wir müssen die Formel auch herleiten können. Das habe ich aber irgendwie nicht verstanden.