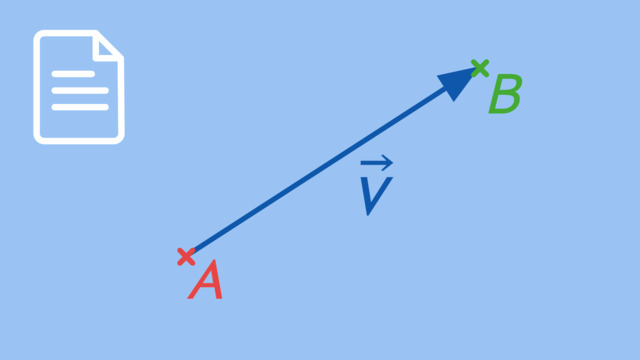
Was ist ein Vektor?

Was ist ein Vektor? Übung

• Vervollständige den Text zu Vektoren.

  Tipps

  Die Besonderheit von Vektoren ist, dass sie Größen beschreiben, die eine Richtung haben.

  Alle drei Vektoren im Bild sind gleich, obwohl sie an verschiedenen Stellen des Koordinatensystems sind. Was ist bei einem Vektor wichtig?

  Lösung

  Der Vektor von Punkt $A$ nach $B$ beschreibt im Allgemeinen eine Verschiebung des Punktes $A$ in den Punkt $B$. Sie wird durch einen Pfeil dargestellt, der an jeden beliebigen Punkt angesetzt werden kann. Vektoren sind also nicht ortsgebunden. Solange zwei Vektoren in Länge und Richtung übereinstimmen, sind diese beiden Vektoren gleich. Mithilfe von nur einem Vektoren lassen sich daher Verschiebungen von gesamten Figuren, wie z.B. Dreiecken, beschreiben. Dabei wird jeder Punkt der Figur mit dem Vektor verschoben.

  Der Vektor, der von Punkt $A$ zu Punkt $B$ zeigt, wird Verbindungsvektor $\overrightarrow{AB}$ genannt. Außerdem heißt der Vektor $\overrightarrow{BA}$, der genau in die entgegengesetzte Richtung zeigt, Gegenvektor von $\overrightarrow{AB}$. Dieser verbindet ebenfalls die Punkte $B$ und $A$, zeigt aber in die entgegengesetzte Richtung.

• Gib die richtige Definition der verschiedenen Begriffe an.

  Tipps

  Jeder Vektor hat eine Länge und eine Richtung und kann als Pfeil dargestellt werden. Die einzige Ausnahme ist der Nullvektor.

  Ein Vektor zwischen zwei Punkten beschreibt den Weg, um von einem Punkt zum anderen zu gelangen.

  Bei einem Ortsvektor wird der Weg vom Koordinatenursprung zu einem Punkt beschrieben.

  Lösung

  Ein Ortsvektor $\overrightarrow{OA}$ ist der Vektor, der die Bewegung beschreibt, um vom Koordinatenursprung $O$ zu einem Punkt $A$ zu kommen. Beispielsweise haben wir den Punkt $A$ mit den Koordinaten $A(2 | 4 )$. Da der Koordinatenursprung $O$ die Koordinaten $O(0|0)$ hat, ergibt sich für den Ortsvektor $\overrightarrow{OA} = \begin{pmatrix} 2\\4 \end{pmatrix}$.

  Ein Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der die Verschiebung von einem Punkt $A$ zu einem Punkt $B$ beschreibt. Er wird durch die Differenz der beiden Ortsvektoren berechnet: $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.
  Für die konkreten Punkte $A(3|1)$ und $B(1|0)$ ergibt sich beispielsweise der Verbindungsvektor $\overrightarrow{AB}$:

  $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}= \begin{pmatrix} 1\\0 \end{pmatrix} - \begin{pmatrix} 3\\1 \end{pmatrix} =\begin{pmatrix} -2\\-1 \end{pmatrix}$.

  Ein Gegenvektor $\overrightarrow{BA}$ ist der gleiche Vektor wie der Verbindungsvektor $\overrightarrow{AB}$, aber mit umgekehrter Richtung. Das bedeutet, dass er die Bewegung von einem Punkt $B$ zum Punkt $A$ beschreibt. Er entspricht dem Verbindungsvektor mit umgekehrten Vorzeichen: $\overrightarrow{BA}= - \overrightarrow{AB}$.
  Der Gegenvektor zu dem Verbindungsvektor $\overrightarrow{AB} = \begin{pmatrix} -2\\-1 \end{pmatrix}$ ist der Vektor: $\overrightarrow{BA}= \begin{pmatrix} 2\\1 \end{pmatrix}$.

  Der Nullvektor $\vec{o}= \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}$ ist der einzige Vektor, der keine Länge und damit auch keine Richtung besitzt. Man kann ihn nicht zeichnen, da alle seine Koordinaten null sind.

• Bestimme den Verbindungsvektor.

  Tipps

  Um einen Verbindungsvektor zu bestimmen, rechnen wir "Endpunkt minus Anfangspunkt".

  Mit "Endpunkt minus Anfangspunkt" sind die Ortsvektoren der jeweiligen Punkte gemeint. Zum Beispiel berechnen wir den Verbindungsvektor zwischen den Punkten $A(0|1)$ und $B(1|4)$ mit:

  $\overrightarrow{AB} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix}$.

  Ein Ortsvektor ist der Vektor, der von dem Koordinatenursprung $O$ in Richtung des Punktes zeigt. Da aber der Koordinatenursprung die Koordinaten $O(0\vert0)$ hat, sind die Einträge des Ortsvektors einfach die Koordinaten des Punktes selbst.

  Lösung

  Der Verbindungsvektor $\overrightarrow{AB}$ zwischen den beiden Punkten $A$ und $B$ wird als Differenz der Ortsvektoren berechnet:
  $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$. Damit wir uns das besser merken, sprechen wir dabei von "Endpunkt minus Anfangspunkt".
  Die Ortsvektoren von $A$ und $B$ sind die Vektoren, die vom Koordinatenursprung $O$ in Richtung der jeweiligen Punkte zeigen. Da aber der Koordinatenursprung $O$ die Koordinaten $O(0\vert0)$ besitzt, sind die Ortsvektoren der Punkte einfach die Koordinaten der jeweiligen Punkte selbst.
  Das bedeutet, für $\overrightarrow{OA}$ und $\overrightarrow{OB}$ ergibt sich:

  $ \overrightarrow{OA} = \begin{pmatrix} 5 \\1 \end{pmatrix}$ und $\ \overrightarrow{OB} = \begin{pmatrix} 2 \\4 \end{pmatrix}$.

  Insgesamt ergibt das für den Verbindungsvektor

  $\overrightarrow{AB} = \begin{pmatrix} 2 \\4 \end{pmatrix} - \begin{pmatrix} 5 \\1 \end{pmatrix} = \begin{pmatrix} 2-5 \\ 4-1 \end{pmatrix}= \begin{pmatrix} -3 \\3 \end{pmatrix}$.

• Ermittle die Vektoren zu den gegebenen Punkten.

  Tipps

  Der Verbindungsvektor $\overrightarrow{AC}$ lässt sich beispielsweise so ausrechnen:

  $\overrightarrow{AC} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} - \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1-2 \\ 1-(-2) \\ 0-1 \end{pmatrix} = \begin{pmatrix} -1 \\ 3 \\ -1 \end{pmatrix}$

  Vertauschen wir die Reihenfolge der Ortsvektoren bei der Differenz, berechnen wir den Gegenvektor von dem Vektor, den wir eigentlich ausrechnen wollen. Zum Beispiel wird mit $\overrightarrow{OA} - \overrightarrow{OB}$ der Gegenvektor $\overrightarrow{BA}$ zu $\overrightarrow{AB}$ berechnet.

  Um den Gegenvektor schnell auszurechnen, können wir ausnutzen, dass die Vorzeichen des Verbindungsvektors nur umgedreht werden müssen. Das bedeutet, wir multiplizieren den Verbindungsvektor mit $-1$ und erhalten den Gegenvektor.

  Lösung

  Mit den gegebenen Punkten $A(2 \vert {-}2 \vert 1)$,$B(0 \vert 3 \vert1)$ und $C(1 \vert 1 \vert 0)$ können wir zunächst die Ortsvektoren der Punkte aufstellen. Diese sind:

  $\overrightarrow{OA} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix}$, $\overrightarrow{OB} = \begin{pmatrix} 0\\3\\1 \end{pmatrix}$, $\overrightarrow{OC} = \begin{pmatrix} 1\\1\\0 \end{pmatrix}$.

  Anschließend können die verschiedenen Verbindungsvektoren durch die Differenz der Ortsvektoren bestimmt werden. Es gilt:

  $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix} 0\\3\\1 \end{pmatrix} - \begin{pmatrix} 2\\-2\\1 \end{pmatrix} = \begin{pmatrix} 0-2\\3-(-2)\\1-1 \end{pmatrix}= \begin{pmatrix} -2\\5\\0 \end{pmatrix}$,

  $\overrightarrow{BA} = \overrightarrow{OA} - \overrightarrow{OB} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix} - \begin{pmatrix} 0\\3\\1 \end{pmatrix} = \begin{pmatrix} 2-0\\(-2) - 3\\1-1 \end{pmatrix} = \begin{pmatrix} 2\\-5\\0 \end{pmatrix}$,

  $\overrightarrow{CA} = \overrightarrow{OA} - \overrightarrow{OC} = \begin{pmatrix} 2\\-2\\1 \end{pmatrix} - \begin{pmatrix} 1\\1\\0 \end{pmatrix} = \begin{pmatrix} 2-1\\(-2)-1\\1-0 \end{pmatrix} = \begin{pmatrix} 1\\-3\\1 \end{pmatrix}$,

  $\overrightarrow{BC} = \overrightarrow{OC} - \overrightarrow{OB} = \begin{pmatrix} 1\\1\\0 \end{pmatrix} - \begin{pmatrix} 0\\3\\1 \end{pmatrix} = \begin{pmatrix} 1-0\\1-3\\0-1 \end{pmatrix} = \begin{pmatrix} 1\\-2\\-1 \end{pmatrix}$.

  Der Vektor $\overrightarrow{BA}$ ist der Gegenvektor zum Verbindungsvektor $\overrightarrow{AB}$. Wir berechnen ihn, indem wir die Ortsvektoren in der Differenz vertauschen. Das ist äquivalent dazu, die Vorzeichen des Verbindungsvektors $\overrightarrow{AB}$ umzudrehen bzw. den Vektor $\overrightarrow{AB}$ mit $-1$ zu multiplizieren.

• Berechne den Verbindungsvektor zwischen den Punkten $A$ und $B$.

  Tipps

  Der Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der von Punkt $A$ in Richtung des Punktes $B$ zeigt.

  Der Verbindungsvektor $\overrightarrow{AB}$ wird durch die Differenz der Ortsvektoren von $A$ und $B$ berechnet. Es gilt also: $ \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.

  Die Formel zum Berechnen des Verbindungsvektors $\overrightarrow{AB}$ kannst du dir gut merken, indem du "Endpunkt minus Anfangspunkt" rechnest.

  Lösung

  Der Verbindungsvektor $\overrightarrow{AB}$ ist der Vektor, der von Punkt $A$ in Richtung des Punktes $B$ zeigt. Er wird durch die Differenz der Ortsvektoren von $A$ und $B$ berechnet. Das bedeutet, es gilt: $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.
  Diese Formel kannst du dir gut merken, indem du dir "Endpunkt minus Anfangspunkt" einprägst.

  Für den Verbindungsvektor $\overrightarrow{AB}$ zwischen den Punkten $A(2\vert2\vert2)$ und $B(3\vert 4 \vert 3)$ ergibt sich:
  $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix} 3\\ 4\\3 \end{pmatrix} - \begin{pmatrix} 2\\ 2\\2 \end{pmatrix} = \begin{pmatrix} 3 - 2\\ 4 - 2\\3 - 2 \end{pmatrix} = \begin{pmatrix} 1\\ 2\\1 \end{pmatrix}$.

• Entscheide, ob die Aussagen zu den Vektoren der Pyramide zutreffen.

  Tipps

  Es gibt drei korrekte Antworten.

  Um dir die Koordinaten der Pyramide besser vorzustellen, solltest du versuchen, sie in einem dreidimensionalen Koordinatensystem zu zeichnen.

  Zwei Vektoren sind dann gleich, wenn sie in Länge und Richtung übereinstimmen. Das heißt, dass sie gleich sein können, obwohl sie zwei unterschiedliche Kanten der Pyramide beschreiben.

  Lösung

  Bei der Pyramide ist der Eckpunkt $D$ der Koordinatenursprung, was das Untersuchen der Antworten vereinfacht. Bevor wir damit anfangen, muss klar sein, dass zwei Vektoren nur gleich sind, wenn sie in Länge und Richtung übereinstimmen. Sie sind nicht ortsgebunden und können von jedem Punkt ausgehen.

  Wir überprüfen, ob die einzelnen Antworten bei der Aufgabe stimmen:

  Antwort 1: Der Ortsvektor $\overrightarrow{OD}$ ist der Nullvektor $\vec{o} = \begin{pmatrix} 0\\0\\0\end{pmatrix}$.
  Der Eckpunkt $D$ der Pyramide liegt hier direkt im Koordinatenursprung. Der Ortsvektor ist der Nullvektor. Diese Antwort stimmt.

  Antwort 2: Der Verbindungsvektor $\overrightarrow{AE}$ ist $\overrightarrow{AE} = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix}$.
  Die Antwort ist korrekt. Den Verbindungsvektor berechnen wir mit: $\overrightarrow{AE} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\0 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix}$.

  Antwort 3: Die Verbindungsvektoren $\overrightarrow{AD}$ und $\overrightarrow{BC}$ sind gleich.
  Diese Antwort stimmt, denn die beiden Vektoren stimmen in Länge und Richtung überein. Es gilt:
  $ \overrightarrow{AD} = \overrightarrow{BC} = \begin{pmatrix} -2 \\ 0 \\ 0 \end{pmatrix}$.

  Antwort 4: Der Vektor $\overrightarrow{DA}$ ist der Gegenvektor zum Verbindungsvektor $\overrightarrow{CB}$.
  Der Vektor $\overrightarrow{DA} =\begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $ und der Vektor $\overrightarrow{CB} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $ unterscheiden sich nicht nur um den Faktor ${-}1$. Der Vektor $\overrightarrow{DA}$ ist nicht der Gegenvektor. Die beiden Vektoren sind hier identisch. Diese Aussage ist nicht korrekt.

  Antwort 5: Der Verbindungsvektor $\overrightarrow{BE}$ ist $\overrightarrow{BE} = \begin{pmatrix} 1 \\ 1 \\ -2 \end{pmatrix}$.
  Die Antwort stimmt nicht. Den Verbindungsvektor berechnen wir mit: $\overrightarrow{BE} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\2 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 2 \end{pmatrix}$.

  Antwort 6: Der Ortsvektor $\overrightarrow{OC}$ ist der Gegenvektor zum Ortsvektor $\overrightarrow{OA}$.
  Der Ortsvektor $\overrightarrow{OC} =\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} $ ist nicht der Gegenvektor des Ortsvektors $\overrightarrow{OA} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} $, da sie sich nicht um den Faktor ${-}1$ unterscheiden. Diese Aussage ist nicht korrekt.