Geradengleichungen im Raum
In der Geometrie werden Punkt, Geraden und Ebenen sowie deren Lagebeziehungen zueinander untersucht. Hierfür musst du erst einmal die Geradengleichung aufstellen.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Geraden in der Ebene
Wir beginnen mit Geraden in der Ebene. Du kennst Geraden als Funktionsgraphen von linearen Funktionen. Eine lineare Funktionsgleichung ist gegeben durch $f(x)=m\cdot x+n$. Dabei ist $m$ der Anstieg und $n$ der $y$-Achsenabschnitt der zugehörigen Geraden.
Eine solche Gerade kann auch in Form einer Parametergleichung, Normalengleichung oder Koordinatengleichung angegeben werden. Wir behandeln im Folgenden jeweils die lineare Funktion $f$ mit $f(x)=2x+3$.
Die Parametergleichung
Für die Parametergleichung benötigst du
- entweder zwei Punkte
- oder einen Punkt und einen Vektor, den sogenannten Richtungsvektor.
Du bestimmst zwei Punkte, die auf dem Funktionsgraphen zu $f$ liegen, zum Beispiel $(1|5)$ sowie $(3|9)$. Diese Punkte erhältst du jeweils durch Vorgabe eines $x$-Wertes, welchen du in die Funktionsgleichung einsetzt. So erhältst du den zugehörigen $y$-Wert.
So sieht eine Parametergleichung aus: $g:\vec x=\vec a+r\cdot \vec u$. Dabei ist
- $\vec x$ ein Vektor, der auf einen beliebigen Punkt der Geraden zeigt,
- $\vec a$ ein Vektor, der auf einen gegebenen Punkt der Geraden zeigt, der Stützvektor,
- $\vec u$ der Richtungsvektor und
- $r\in\mathbb{R}$ ein Parameter.
So erhältst du für das obige Beispiel
$g:\vec x=\begin{pmatrix} 1 \\ 5 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$
Der Richtungsvektor ist der Verbindungsvektor der beiden Punkte. Dies ist die sogenannte Zweipunktgleichung einer Geraden.
Die Normalengleichung
Für die Normalengleichung in der Ebene benötigst du einen Vektor, der senkrecht zu dem Richtungsvektor steht. Ein solcher Vektor ist zum Beispiel wie folgt gegeben:
$\vec n= \begin{pmatrix} 2 \\ -1 \end{pmatrix}$
Nun kannst du wie folgt die Normalengleichung aufstellen:
$g:\left(\vec x-\begin{pmatrix} 1 \\ 5 \end{pmatrix}\right)\star \begin{pmatrix} 2 \\ -1 \end{pmatrix}=0$
Der Operator $\star$ zeigt das Skalarprodukt von Vektoren an.
Die Koordinatengleichung
Die Koordinatengleichung erhältst du durch Umformung der Funktionsgleichung. Die beiden Variablen stehen dabei auf der linken Seite der Gleichung und auf der rechten Seite steht eine Konstante. Subtrahiere bei der Gleichung $y=2x+3$ den Term $2x$. So kommst du zu $-2x+y=3$.
Bei Geraden im Raum sieht dies so ähnlich aus. Jedoch gibt es keinen Normalenvektor und damit auch keine Normalengleichung und auch keine Koordinatengleichung.
Geraden im Raum
Geraden im Raum sind ebenfalls entweder durch einen Punkt und einen Vektor oder durch zwei Punkte gegeben. Eine Parametergleichung sieht ebenso aus wie die in der Ebene. Nur haben die Vektoren dieses Mal drei statt zwei Koordinaten. Es ist also:
$g:\vec x=\vec a+r\cdot \vec u$
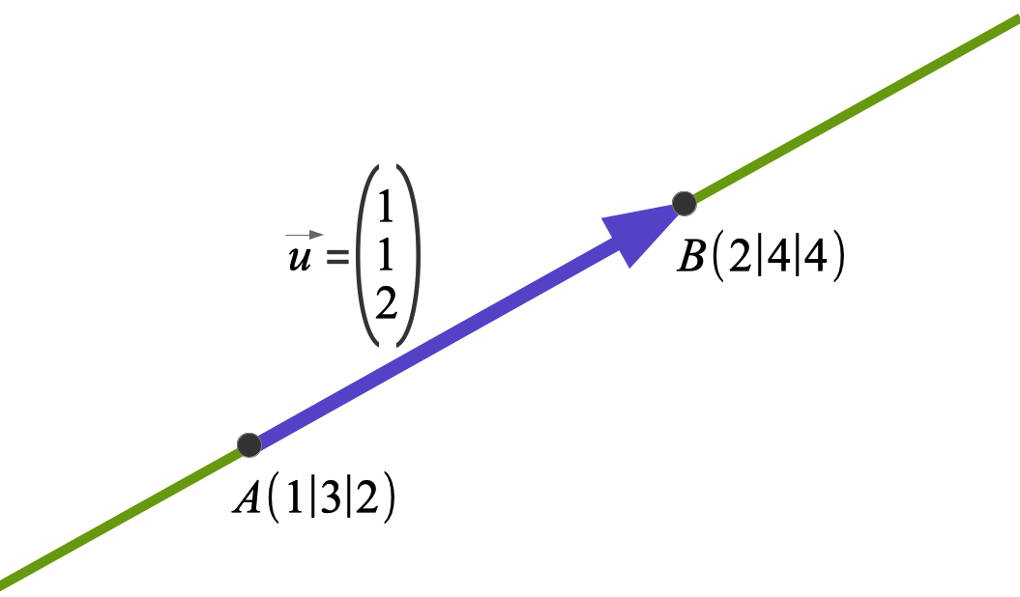
Die Bedeutung der einzelnen Größen ist die gleiche. Wir schauen uns das Beispiel der folgenden Geraden durch die beiden Punkte $A(1|3|2)$ sowie $B(2|4|4)$ an. Du stellst nun die Zwei-Punkt-Gleichung dieser Geraden auf.
$g:\vec x=\begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$
Anwendungsaufgaben
Hier siehst du noch einige mögliche Anwendungsaufgaben im Zusammenhang mit Geraden.
Die Punktprobe
Du sollst prüfen, ob ein Punkt auf einer Geraden liegt. Dies führt zu der Punktprobe. Hierfür setzt du den Ortsvektor des Punktes für $\vec x$ in die obige Geradengleichung ein. So erhältst du ein lineares Gleichungssystem mit drei Gleichungen und einer Unbekannten, dem Parameter. Ist dieses Gleichungssystem lösbar, dann liegt der Punkt auf der Geraden, ansonsten nicht.
Die vektorielle Darstellung einer Strecke
Da die obige Gerade durch die beiden Punkte $A$ und $B$ gegeben ist, bedeutet dies für den Parameter $r$:
- $r=0$ entspricht dem Punkt $A$.
- $r=1$ entspricht dem Punkt $B$.
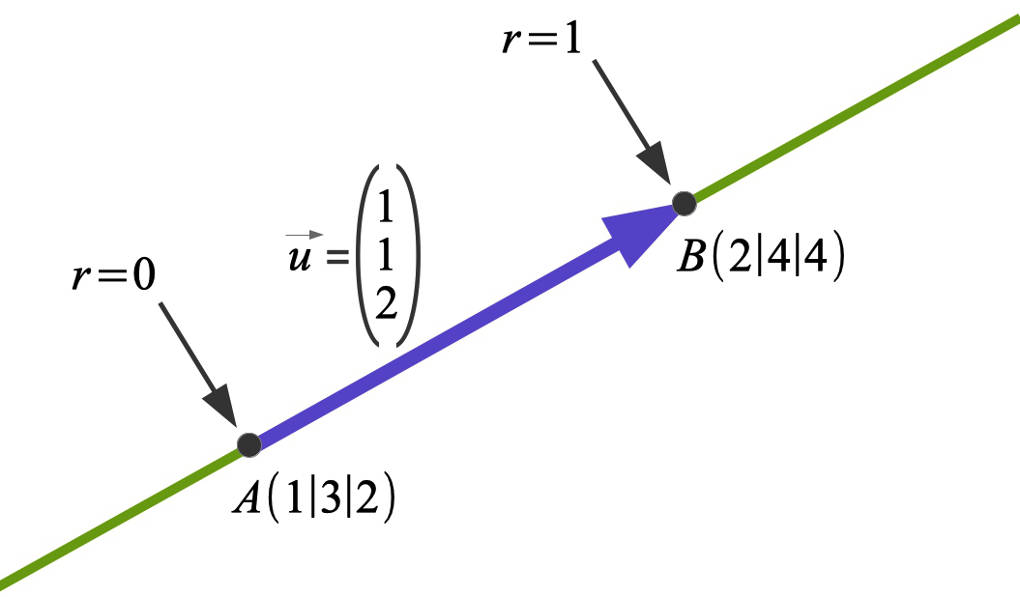
Möchtest du also die Strecke vektoriell angeben, musst du bei der obigen Parametergleichung an den Parameter noch die Bedienung $0\le r\le 1$ knüpfen.
Lagebeziehungen: Gerade - Gerade
Untersuche zunächst die beiden Richtungsvektoren. Sind diese kollinear?
- Falls ja: Die Geraden können identisch oder parallel zueinander sein.
- Falls nein: Die Geraden schneiden sich in einem Punkt oder sie sind windschief.
Für weitere Untersuchungen musst du auch hier Gleichungssysteme lösen.
Aufstellen von Geradengleichungen mit vorgegebenen Eigenschaften
Du weißt nun, wie du eine Gleichung einer Geraden durch zwei Punkte aufstellen kannst. Die Aufgabenstellung könnte auch darin bestehen, dass eine Gerade parallel zu einer anderen durch einen gegebenen Punkt gehen soll. Denke dabei immer daran, dass du einen Stützvektor und einen Richtungsvektor benötigst. Dabei verwendest du die vorgegebenen Eigenschaften.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Geradengleichungen im Raum (3 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Geradengleichungen im Raum (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt








 Geradengleichungen in der Ebene – Überblick
Geradengleichungen in der Ebene – Überblick
 Geradengleichungen in der Ebene – Koordinatengleichung bestimmen
Geradengleichungen in der Ebene – Koordinatengleichung bestimmen
 Normalengleichung in der Ebene
Normalengleichung in der Ebene
 Geradengleichungen in Parameterform im Raum
Geradengleichungen in Parameterform im Raum












