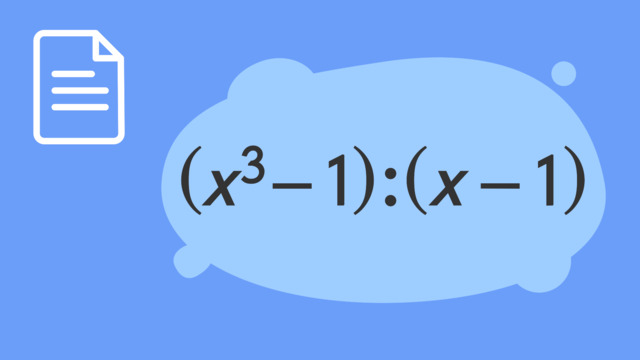Polynomdivision – Erklärung
Entdecke, wie du mit der Polynomdivision komplexe Polynome effektiv zerlegen und Nullstellen berechnen kannst. Dieses mathematische Verfahren hilft dir, Terme zu vereinfachen und tiefer in die Welt der Algebra einzutauchen. Neugierig, wie das funktioniert? Erfahre mehr im folgenden Text!
- Polynomdivision – Definition
- Polynomdivision – Erklärung
- Durchführung der Polynomdivision: 1. Schritt
- Durchführung der Polynomdivision: 2. Schritt
- Durchführung der Polynomdivision: 3. Schritt

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Polynomdivision – Erklärung Übung
-
Vervollständige die Polynomdivision.
TippsDas Vorgehen bei der Polynomdivision entspricht dem Vorgehen bei der schriftlichen Division ganzer Zahlen.
Nachdem der erste Summand des Ergebnisses ermittelt worden ist, muss dieser mit dem Divisor verrechnet werden. Dieser Term wird dann vom Dividenden abgezogen.
LösungWir betrachten die Polynomdivision $\left(x^3+6x^2-x-30\right):(x+3)$ Schritt für Schritt:
1. Zuerst wird der erste Summand $x^3$ des Dividenden durch den ersten Summanden des Divisors $x$ geteilt:
$\frac{x^3}{x}=x^2$
2. Dieses Ergebnis wird hinter dem Gleichheitszeichen aufgeschrieben.
3. Nun wird das Ergebnis $x^2$ mit dem Divisor $x+3$ multipliziert zu $x^3+3x^2$.
4. Das Produkt wird vom Dividenden subtrahiert:
$x^3+6x^2-x-30-\left(x^3+3x^2\right)=3x^2-x-30$
Dies ist der „neue“ Dividend.
5. Es geht weiter wie in Schritt 1:
$\frac{3x^2}{x}=3x$
Dieses Ergebnis wird hinter $x^2$ auf der rechten Seite des Gleichheitszeichens aufgeschrieben.
6. Wieder wird das Ergebnis mit dem Divisor multipliziert:
$3x\cdot (x+3)=3x^2+9x$
7. Das Produkt wird vom Dividenden subtrahiert:
$3x^2-x-30-\left(3x^2+9x\right)=-10x-30$
8. Erneut geht es weiter wie in Schritt 1:
$\frac{-10x}{x}=-10$
Dieses Ergebnis wird hinter $3x$ auf der rechten Seite des Gleichheitszeichens aufgeschrieben.
9. Das Ergebnis wird mit dem Divisor multipliziert:
$-10\cdot (x+3)=-10x-30$
10. Schließlich wird das Produkt von dem Dividenden subtrahiert:
$-10x-30-(-10x-30)=0$
Damit ergibt sich:
$\left(x^3+6x^2-x-30\right):(x+3) = x^2+3x-10$
-
Gib an, was bei der Polynomdivision zu beachten ist.
TippsEs sind zwei Aussagen richtig.
Für eine Division gilt allgemein:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
LösungBei der Polynomdivision wird ein Polynom durch ein anderes geteilt. Ein Polynom kann dadurch in mehrere kleinere Polynome zerlegt werden. Das Vorgehen entspricht im Allgemeinen dem Vorgehen bei der schriftliche Division ganzer Zahlen.
Wir betrachten die einzelnen Aussagen:
- Der Grad des Polynoms des Divisors darf nicht größer sein als der Grad des Polynoms des Dividenden.
- Es darf kein Rest bleiben: Die letzte Zeile ergibt null.
- Beim Dividenden müssen zu Beginn die Summanden nach der Größe der Exponenten sortiert werden.
- Bei der Probe wird das Ergebnis mit dem Dividenden multipliziert.
-
Bestimme das Ergebnis der Polynomdivision.
TippsAchte auf korrekte Vorzeichen.
Beim dritten Beispiel bleibt ein Rest.
LösungWir gehen bei der Polynomdivision nach dem Schema „dividieren – multiplizieren – subtrahieren“ vor. In den einzelnen Beispielen ergibt sich:
Beispiel 1:
$~~~ (x^{3} +x^{2} +8x-28)~:~(x-2) ~=~x^{2} + 3x+14$
$\underline{-(x^{3}-2x^{2})}$
$~~~~~~~~~~~~~\,3x^{2}+8x-28$
$\quad \quad ~ \underline{-(3x^{2}-6x) }$
$\qquad \qquad \quad ~~ 14x-28$
$\qquad \quad \quad ~~ \underline{-(14x-28)}$
$\qquad \qquad \qquad \quad \quad ~~~~0$
Beispiel 2:
$~~~ (6x^{3} - 3x^{2} \qquad ~ + 9)~:~(x + 1)~=~6x^{2} - 9x + 9$
$\underline{- (6x^{3} + 6x^{2})}$
$~~~~~~~~~~~~~~~ \,9x^{2} \qquad ~ + 9$
$\qquad~~~ \underline{- (9x^{2} - 9x) }$
$\qquad \qquad \qquad ~~ \,9x + 9$
$\qquad \qquad \quad ~~\underline{- (9x - 9)}$
$\qquad \qquad \qquad \qquad ~~ ~~0$
Beispiel 3:
$~~~ (12x^{3}+5x^2 ~~~~~~~~~~~~~~ -~10)~:~(x-2)~=~12x^2 + 29x + 58 ~~~ \left(+~\frac{106}{x-2} ~~\text{Rest}\right)$
$\underline{-(12x^{3}-24x^2) }$
$~~~~~~~~~~~~~~~~~ \,29x^2 ~~ ~~~~~~~~~~-~10$
$\qquad ~~~~~ \underline{-(29x^2-58x) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~-58x~ - ~10$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(58x - 116) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+~106$
-
Berechne das Ergebnis der Polynomdivision.
TippsVergiss die Vorzeichen der Zahlen nicht!
Im Dividenden kommt kein $x^2$ vor, aber im Ergebnis schon.
Mache die Probe, falls du unsicher bist.
Lösung$~~~ (2x^{4}+4x^3 ~~~~~~~~~~~~~ -~~x~~ - ~6)~:~(x+3)~=~2x^3 - 2x^2 + 6x + 19 ~~~ \left(-~\frac{63}{x+3} ~~\text{Rest}\right)$
$\underline{-(2x^4+6x^3) }$
$~~~~~~~~~~~ \,-~2x^3 ~~~~~~~~~~~-~~x ~~~ -~6$
$\qquad \underline{-(-~2x^3-6x^2) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~6x^2 - ~~x ~~~- ~6$
$~~~~~~~~~~~~~~~~~~~~~~~\underline{-(~6x^2+18x)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-~19x~- ~6$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(19x+57)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-63$
-
Gib zu jeder Polynomdivision die passende Probe an.
TippsBei der Probe multiplizierst du das Ergebnis der Polynomdivision mit dem Divisor. Dieses Produkt muss gleich dem Dividenden sein.
Für eine Division gilt allgemein:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
Beispiel:
$\underbrace{48}_{\text{Dividend}} : \underbrace{6}_{\text{Divisor}} = \underbrace{8}_{\text{Ergebnis}}$
Wir machen folgende Probe:
$\underbrace{8}_{\text{Ergebnis}} \cdot \underbrace{6}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden – in diesem Fall $48$.
LösungDas Vorgehen bei der Polynomdivision entspricht dem Vorgehen bei der schriftliche Division. Du musst dich also nur an das nachfolgende Schema halten, um auf die richtige Lösung zu kommen:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
Nichtsdestotrotz kann es passieren, dass sich Fehler einschleichen. Um zu überprüfen, ob du richtig gerechnet hast, kannst du die Probe machen. Dazu multiplizierst du das Ergebnis der Polynomdivision mit dem Divisor. Dieses Produkt muss gleich dem Dividenden sein. Dann hast du alles richtig gemacht.
Erste Rechnung:
$\underbrace{(5x^3-17x^2+4x+6)}_{\text{Dividend}} : \underbrace{(x-3)}_{\text{Divisor}} = \underbrace{5x^2-2x-2}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{5x^2-2x-2}_{\text{Quotient}} \cdot \underbrace{(x-3)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $5x^3-17x^2+4x+6$.
Zweite Rechnung:
$\underbrace{(4x^3-5x^2-4x-4)}_{\text{Dividend}} : \underbrace{(x-2)}_{\text{Divisor}} = \underbrace{4x^2+3x+2}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{4x^2+3x+2}_{\text{Quotient}} \cdot \underbrace{(x-2)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $4x^3-5x^2-4x-4$.
Dritte Rechnung:
$\underbrace{(x^3-2x^2-8x+21)}_{\text{Dividend}} : \underbrace{(x+3)}_{\text{Divisor}} = \underbrace{x^2-5x+7}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{5x^2-2x-2}_{\text{Quotient}} \cdot \underbrace{(x+3)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $x^3-2x^2-8x+21$.
-
Überprüfe die Rechnungen.
TippsAuch wenn eine Polynomdivision keinen Rest hat, kann sie einen Fehler enthalten.
Nur eine der vier Rechnungen ist korrekt.
LösungBei der Polynomdivision gibt es einige häufig auftauchende Fehler, die wir vermeiden wollen:
- Vorzeichenfehler
- Fehler in den Potenzen
- Divisor wird nicht korrekt multipliziert
Wir überprüfen nun die gegebenen Beispiele:
Beispiel 1:
$~~~ (10x^{3} + ~~~~ x^{2} + 9)~:~(\color{#FF66FF}{x}$$ + 1)~=~10x^2 - \color{#FF66FF}{9}$
$\underline{- (10x^{3} + 10x^{2})}$
$~~~~~~~~~~~~~~~ \,-9x^{2} + 9$
$\qquad~~~ \color{#FF66FF}{\underline{- (-9x^2 - 9)}}$
$\qquad \qquad \qquad ~~ \,0$
Bei diesem Beispiel wurden beim Multiplizieren die Potenzen falsch notiert. Korrekt lautet die Polynomdivision:
$~~~ (10x^{3}+ ~~~~ x^2 ~~~~~~~~~~~ +9)~:~(x+1)~=~10x^2 - 9x + 9$
$\underline{-(10x^{3}+10x^2)}$
$~~~~~~~~~~~~~~~~~ \,-9x^2 ~~ ~~~~~~~~+9$
$\qquad ~~~~~ \underline{-(-9x^2-9x) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~9x ~+ 9$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(9x+9)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0$
Beispiel 2:
$~~~ (x^{3} -5x^{2} ~~~~~+16x-30)~:~(x\color{#FF66FF}{-}$ $3) ~=~x^{2} \color{#FF66FF}{-}$ $ 2x+22 ~~~ \left(+~\frac{66}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2})} $
$~~~~~~~~~~~~~~\,-2x^{2}+16x-30$
$\quad \quad ~~ \color{#FF66FF}{\underline{-(-2x^{2}-6x) }}$
$\qquad \qquad \qquad ~~~~22x-30$
$\qquad \quad \quad ~~~~~~~ \underline{-(22x-66)}$
$\qquad \qquad \qquad \quad \quad ~~~~+66$
Hier gibt es einen Vorzeichenfehler. Korrekt lautet die Polynomdivision:
$~~~ (x^{3} -5x^{2} ~~~~~+16x-30)~:~(x-3) ~=~x^{2} - 2x+10$
$\underline{-(x^{3}-3x^{2}) }$
$~~~~~~~~~~~~~~\,-2x^{2}+16x-30$
$\quad \quad ~~ \underline{-(-2x^{2}+6x)}$
$\qquad \qquad \qquad ~~~~10x-30$
$\qquad \quad \quad ~~~~~~~ \underline{-(10x-30)}$
$\qquad \qquad \qquad \quad \quad ~~~~~~~~0$
Beispiel 3:
$~~~ (2x^{3} + 6x^{2} ~~-7x + 4)~:~(x+4) ~=~2x^{2} - 2x+1$
$\underline{-(2x^{3}+8x^{2}) }$
$~~~~~~~~~~~~~~\,-2x^{2}-7x+4$
$\quad \quad ~~ \underline{-(-2x^{2}-8x)}$
$\qquad \qquad \qquad ~~~~~~~x+4 $
$\qquad \quad \quad ~~~~~~~~~~ \underline{-(x+4)}$
$\qquad \qquad \qquad \quad \quad ~~~~~~0$
Dieses Beispiel enthält keinen Fehler.
Beispiel 4:
$~~~ (x^{3} +x^{2} ~~~+8x-10)~:~(x-3) ~=~x^{2} + 4x-4 ~~~ \left(-~\frac{22}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2}) }$
$~~~~~~~~~~~~~~\,4x^{2}+8x-10$
$\quad \quad ~~ \underline{-(4x^{2}-12x)}$
$\qquad \qquad \qquad \color{#FF66FF}{-4x}$$-10$
$\qquad \quad \quad ~~~ \underline{-(-4x+12)}$
$\qquad \qquad \qquad \quad \quad ~~-22$
Hier ist die Subtraktion falsch. Korrekt lautet die Polynomdivision:
$~~~ (x^{3} +x^{2} ~~~+8x-10)~:~(x-3) ~=~x^{2} + 4x+20 ~~~ \left(+~\frac{50}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2})}$
$~~~~~~~~~~~~~~\,4x^{2}+8x-10$
$\quad \quad ~~ \underline{-(4x^{2}-12x)}$
$\qquad \qquad \qquad 20x-10$
$\qquad \quad \quad ~~~ \underline{-(20x-60)}$
$\qquad \qquad \qquad \quad \quad ~~~~50$
9.369
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.224
Lernvideos
38.691
Übungen
33.496
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen