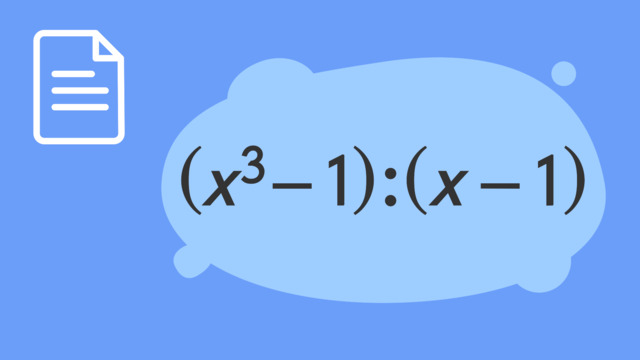Polynomdivision – Erklärung
Entdecke, wie du mit der Polynomdivision komplexe Polynome effektiv zerlegen und Nullstellen berechnen kannst. Dieses mathematische Verfahren hilft dir, Terme zu vereinfachen und tiefer in die Welt der Algebra einzutauchen. Neugierig, wie das funktioniert? Erfahre mehr im folgenden Text!
- Polynomdivision – Definition
- Polynomdivision – Erklärung
- Durchführung der Polynomdivision: 1. Schritt
- Durchführung der Polynomdivision: 2. Schritt
- Durchführung der Polynomdivision: 3. Schritt


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Polynomdivision – Erklärung
Polynomdivision – Definition
Die Polynomdivision ist ein Verfahren in der Mathematik zur Berechnung von Nullstellen und dient der Vereinfachung von Termen.
Bei der Polynomdivision wird, wie der Name bereits andeutet, ein Polynom durch ein anderes Polynom dividiert.
Beispielsweise sind sowohl $-x^2-7x -12$ als auch $x+4$ Polynome. Die Rechnung ${(-x^2-7x -12) : (x+4)}$ stellt demnach eine Polynomdivision dar.
Wusstest du schon?
Die Polynomdivision hat Ähnlichkeiten mit der schriftlichen Division, die du in der Grundschule gelernt hast. Wenn du dich also an die „Zahlen untereinander“ und das „Restaufschreiben“ erinnerst, dann hast du schon die halbe Miete bei der Polynomdivision gewonnen!
Polynomdivision – Erklärung
Wir wollen die Durchführung der Polynomdivision anhand eines Funktionsterms erklären, dessen Nullstellen gefunden werden sollen. So können wir einerseits das schrittweise Vorgehen der Polynomdivision zeigen und andererseits den Nutzen für die Nullstellensuche erläutern.
Durchführung der Polynomdivision: 1. Schritt
An einem Beispiel lässt sich das Verfahren am besten verstehen. Wollen wir beispielsweise die Nullstellen der kubischen Funktion
$f(x)=x^{3}-2x^{2}-5x+6$
finden, so müssen wir zunächst eine erste Nullstelle der Funktion ermitteln. Diese Nullstelle kann durch Raten oder durch Zeichnen der Funktion gefunden werden.
Um eine Nullstelle zu raten, ermitteln wir am besten die Teiler des konstanten Gliedes, also des Terms ohne Faktor $x$ (hier im Beispiel die $6$), und setzen diese Werte in die Funktionsgleichung für $x$ ein. Ist das Ergebnis $0$, haben wir die erste Nullstelle gefunden. Mögliche Teiler sind in unserem Beispiel $1$, $-1$, $2$, $-2$, $3$, $-3$, $6$ und $-6$.
Setzen wir zum Beispiel für $x$ die $1$ in die Funktionsgleichung ein, erhalten wir:
$f(1)=1^{3} -2 \cdot 1^{2} - 5 \cdot 1 + 6 = 1 -2-5+6=0$
Das bedeutet, dass mit $x_1=1$ die erste Nullstelle der Funktion gefunden ist.
Der erste Linearfaktor der Funktion $f(x)=x^{3}-2x^{2}-5x+6$ ist also $(x-1)$.
Eine mögliche Linearfaktorzerlegung der Funktion lautet damit:
$f(x)=x^{3}-2x^{2}-5x+6 = (x-1) \cdot y \cdot z$
Die Variablen $y$ und $z$ stellen dabei die noch unbekannten, weiteren Linearfaktoren dar. Es muss insgesamt drei Linearfaktoren geben, da es sich um eine kubische Funktion, also eine Funktion dritten Grades, handelt.
Setzen wir in den ersten Linearfaktor die $1$ ein, also den Wert der ersten Nullstelle, ist dieser Faktor $0$. Der Funktionswert ist dann auch $0$, egal, was die anderen Linearfaktoren ergeben, da hier mit $0$ multipliziert wird. (Das ist der Satz vom Nullprodukt.)
Nun müssen wir die anderen beiden Linearfaktoren finden, um weitere Nullstellen bestimmen zu können. Dafür nutzen wir die Polynomdivision.
Durchführung der Polynomdivision: 2. Schritt
Teilen wir den Funktionsterm durch den bereits gefundenen Linearfaktor, so bleiben auf der rechten Seite die beiden bisher noch nicht gefundenen Linearfaktoren übrig:
$\begin{array}{ccccll} x^{3}-2x^{2}-5x+6 & & & = & (x-1) \cdot y \cdot z & \quad\big\vert~: (x-1) \\[2pt] (x^{3}-2x^{2}-5x+6) & : & (x-1) & = & y \cdot z & \end{array}$
Die Divisionsaufgabe auf der linken Seite wird als Polynomdivision bezeichnet:
$(x^{3}-2x^{2}-5x+6) : (x-1)$
Das Vorgehen funktioniert folgendermaßen:
1. Teile den ersten Term des Dividenden ${\color{#669900}{x^3}}-2x^2-5x+6$ durch den ersten Term des Divisors ${\color{#669900}{x}}-1$:
${\color{#669900}{x^3}} : {\color{#669900}{x}} = {\color{#669900}{x^2}}$
2. Das Ergebnis ${\color{#669900}{x^2}}$ schreibst du hinter das Gleichheitszeichen:
$({\color{#669900}{x^3}}-2x^2-5x+6) : ({\color{#669900}{x}}-1) = {\color{#669900}{x^2}}$
3. Nun multiplizierst du den Divisor ${\color{#669900}{(x-1)}}$ mit dem Zwischenergebnis ${\color{#669900}{x^2}}$, also:
${\color{#669900}{(x-1)}} \cdot {\color{#669900}{x^2}} = {\color{#669900}{x^3-x^2}}$
Dieses Ergebnis schreibst du stellengerecht unter das erste Polynom:
$\begin{array}{lcccl} (x^3-2x^2-5x+6) & : & {\color{#669900}{(x-1)}} & = & {\color{#669900}{x^2}} \\[2pt] ({\color{#669900}{x^3-x^2}}) & & & & \end{array}$
4. Subtrahiere jetzt $x^3-x^2$ vom ersten Polynom:
$\begin{array}{lcccl} ~~~(x^3-2x^2-5x+6) & : & (x-1) & = & x^2 \\[2pt] \underline{{\color{#669900}{-(}} x^3-x^2 {\color{#669900}{)}}} & & & & \end{array}$
Schreibe das Ergebnis unter den Strich:
$\begin{array}{lcccl} ~~~(x^3-2x^2-5x+6) & : & (x-1) & = & x^2 \\[2pt] \underline{{\color{#669900}{-(}} x^3-x^2 {\color{#669900}{)}}} & & & & \\[2pt] ~~~~\,0~-\,x^2 & & & & \end{array}$
Du merkst, dass der erste Term $x^3$ dabei wegfällt. Das muss so sein.
Bringe nun auch die restlichen Terme des ersten Polynoms nach unten:
$\begin{array}{lcccl} ~~~(x^3-2x^2{\color{#669900}{-5x+6}}) & : & (x-1) & = & x^2 \\[2pt] \underline{-(x^3-x^2)} & & & & \\[2pt] ~~~~~~~~~\,-\,x^2{\color{#669900}{-5x+6}} & & & & \end{array}$
Mit der neuen Zeile hast du nun einen neuen Dividenden.
5. Nun beginnt die Division von vorne. Teile jetzt den ersten Term des neuen Dividenden, also ${\color{#669900}{-x^2}}$, durch den ersten Term des Divisors, also wieder durch ${\color{#669900}{x}}$, und ergänze das Ergebnis rechts:
$\begin{array}{lcccl} ~~~(x^3-2x^2-5x+6) & : & ({\color{#669900}{x}}-1) & = & x^2 {\color{#669900}{-x}} \\[2pt] \underline{-(x^3-x^2)} & & & & \\[2pt] ~~~~~~~~~\,{\color{#669900}{-\,x^2}}-5x+6 & & & & \end{array}$
Wiederhole die Schritte 1. bis 4., bis am Ende $0$ bei der Subtraktion herauskommt. Die gesamte Polynomdivision sieht dann wie folgt aus:
$\begin{array}{lcccl} ~~~(x^3-2x^2-5x+6) & : & (x-1) & = & x^2-x-6 \\[2pt] \underline{-(x^3-x^2)} & & & & \\[2pt] ~~~~~~~~~\,-\,x^2-5x+6 & & & & \\[2pt] ~~~~~~\underline{-(-x^2+x)} & & & & \\[2pt] ~~~~~~~~~~~~~~~~~~-\,6x+6 & & & & \\[2pt] ~~~~~~~~~~~~~~\underline{-(-6x+6)} & & & & \\[2pt] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0 \end{array}$
Beachte, dass wir gleiche Potenzen immer untereinander schreiben, damit das Subtrahieren der Zeilen übersichtlich bleibt. Nicht bei jeder Polynomdivision kommt am Ende $0$ heraus, das heißt, nicht jede Polynomdivision geht genau auf. Darauf kommen wir noch zurück.
Durchführung der Polynomdivision: 3. Schritt
Um die restlichen Nullstellen $x_2$ und $x_3$ zu finden, müssen wir nun nur noch die Lösungen des Polynoms ${x^2-x-6=0}$ bestimmen. Das ist nur noch ein Polynom 2. Grades, was im Vergleich zum Polynom davor eine deutlich einfachere Aufgabe darstellt.
Kennst du das?
Vielleicht hast du schon einmal versucht, ein großes Puzzle zusammenzusetzen. Zu Beginn ist es oft schwierig, die Teile richtig zuzuordnen. Doch sobald du ein paar Teile gefunden hast, die zusammenpassen, klappt es zunehmend besser. Die Polynomdivision funktioniert ähnlich: Zuerst zerlegst du ein komplexes Polynom Schritt für Schritt in einfachere Teile, bis du die Lösung findest. Es ist wie das Zusammensetzen eines mathematischen Puzzles.
Da es sich hierbei um eine quadratische Gleichung handelt, können wir dafür zum Beispiel die
$x_{2,3}=-\left(-\dfrac{1}{2}\right) \pm\sqrt{{\left(-\dfrac{1}{2}\right)}^2-(-6)}$
$\Rightarrow x_{2}=3$
$\Rightarrow x_{3}=-2$
Die Lösungen dieses Polynoms sind also $x_2=3$ und $x_3=-2$.
Damit haben wir nun alle Nullstellen der kubischen Funktion $f(x)=x^{3}-2x^{2}-5x+6$ gefunden. Die Nullstellen sind $x_1=1$, $x_2=3$ und $x_3=-2$.
In Linearfaktorzerlegung lautet die Funktion also:
$f(x)=x^{3}-2x^{2}-5x+6=(x-1) \cdot (x-3) \cdot (x+2)$
So wie die
Polynomdivision – Beispiel
Anhand des Beispiels $(-x^2-7x -12) : (x+4)$ wollen wir nun das Vorgehen bei der Polynomdivision noch einmal im Schnelldurchlauf durchgehen:
1. Zunächst wird der erste Summand $-x^2$ des Dividenden durch den ersten Summanden $x$ des Divisors geteilt:
$\dfrac{-x^2}{x}={\color{#669900}{-x}}$
2. Dieses Ergebnis wird hinter dem Gleichheitszeichen aufgeschrieben:
$(-x^2-7x-12) : (x+4) = {\color{#669900}{-x}}$
3. Nun wird das Ergebnis ${\color{#669900}{-x}}$ mit dem gesamten Divisor $(x+4)$ multipliziert:
${\color{#669900}{-x}} \cdot (x+4) = -x^2-4x$
Fehleralarm
Ein häufiger Fehler betrifft das Vorzeichen beim Subtrahieren von Termen. Es ist wichtig, bei der Polynomdivision das richtige Vorzeichen zu setzen, sonst stimmt das Ergebnis nicht.
4. Das Produkt wird vom Dividenden subtrahiert:
$(-x^2-7x-12)-(-x^2-4x)={\color{#669900}{-3x-12}}$
Dies ist der neue Dividend.
5. Es geht weiter wie in Schritt 1, der erste Summand des neuen Dividenden wird also wieder durch $x$ geteilt:
$\dfrac{-3x}{x}={\color{#669900}{-3}}$
Dieses Ergebnis wird hinter $-x$ auf der rechten Seite des Gleichheitszeichens aufgeschrieben:
$(-x^2-7x-12) : (x+4) = -x{\color{#669900}{-3}}$
6. Wieder wird das Ergebnis mit dem gesamten Divisor multipliziert:
${\color{#669900}{-3}} \cdot (x+4)=-3x-12$
7. Schließlich wird das Produkt vom Dividenden subtrahiert:
$-3x-12-(-3x-12)={\color{#669900}{0}}$
Damit ist die Polynomdivision aufgegangen und als Ergebnis bleibt:
$(-x^2-7x-12) : (x+4) = -x-3$
In der folgenden Abbildung sind alle beschriebenen Rechenschritte auf einen Blick dargestellt:

Polynomdivision mit Rest
Bei den ersten beiden Rechnungen kam zum Schluss immer $0$ heraus, das heißt, die Polynomdivision ging genau auf. Dies muss nicht immer so sein.
Bei der Polynomdivision $(-x^2+2x+2) : (x+1)$ bleibt beispielsweise $-1$ übrig, wie du in der Abbildung der entsprechenden Rechnung sehen kannst:

Wenn die Polynomdivision nicht aufgeht, hat sie einen Rest. Dieser wird am Ende des Lösungsterms als Quotient aus der Restzahl (oder dem Restterm) und dem Divisor der Polynomdivision angegeben.
Bei der dargestellten Polynomdivision lautet der gesamte Lösungsterm demnach wie folgt:
$(-x^2+2x+2) : (x+1) = -x+3+\dfrac{-1}{x+1}$
Ein Rest tritt immer dann auf, wenn die Polynomdivision nicht aufgeht und der Grad des Divisors höher ist als der Grad des letzten Dividenden (also des Restterms bzw. der Restzahl).
Polynomdivision – Nullstellen
Wir haben bereits gesehen, dass eine häufige Anwendung der Polynomdivision das Bestimmen von Nullstellen von Polynomen ist, deren Grad höher als $2$ ist. Sehen wir uns dazu noch ein weiteres Beispiel an:
Es sei bereits bekannt, dass die Funktion $f$ mit $f(x)=-x^3+3x^2-2$ eine Nullstelle bei $x_1=1$ habe. (Dies kann durch Einsetzen überprüft werden.)
Diese kubische Funktion könnte noch zwei weitere Nullstellen besitzen. Um diese zu ermitteln, dividieren wir den kubischen Funktionsterm durch den Linearfaktor $(x-1)$.
(Eine bereits bekannte Nullstelle wird immer von $x$ subtrahiert, um den entsprechenden Linearfaktor zu erhalten).
Die entsprechende Polynomdivision ist in folgender Abbildung dargestellt:

Der quadratische Term, der das Ergebnis dieser Polynomdivision darstellt, kann nun gleich $0$ gesetzt werden und mithilfe der
$x_{2,3}=-(-2)\pm\sqrt{{\left(-\dfrac{2}{2}\right)}^2-(-2)}$
$\Rightarrow x_{2}=2+\sqrt{3} \approx 3{,}73$
$\Rightarrow x_{3}=2-\sqrt{3} \approx 0{,}27$
Die Funktion $f$ kann also in folgenden Linearfaktoren zerlegt werden:
$f(x)=-x^3+3x^2-2=(x-1) \cdot (x-2-\sqrt{3}) \cdot (x-2+\sqrt{3})$
Polynomdivision – Aufgaben
Du kannst hier noch einige weitere Aufgaben üben und dir dann die Lösungen ansehen:
Ausblick – das lernst du nach Polynomdivision – Erklärung
Vertiefe dein Verständnis für Polynome und lerne, wie du Nullstellen durch Polynomdivision bestimmen kannst. Erfahre, wie nützlich die Polynomdivision in der Untersuchung von Funktionen im Rahmen der Kurvendiskussion sein kann.
Wenn du das Gelernte direkt anwenden möchtest, dann schau dir den Übungstext zur Polynomdivision an.
Zusammenfassung – Polynomdivision
- Die Polynomdivision ist ein Verfahren, bei dem ein Polynom durch ein anderes Polynom dividiert, also geteilt, wird.
- Die Polynomdivision wird angewendet, um Funktionen höheren Grades zu faktorisieren, also in Linearfaktoren zu zerlegen.
- Die Linearfaktorzerlegung dient vor allem der Bestimmung der Nullstellen eines Polynoms. Ist eine Nullstelle bereits bekannt (oder kann erraten werden), kann eine Polynomdivision mit dem Linearfaktor dieser Nullstelle als Divisor durchgeführt werden, um das Polynom weiter zu zerlegen.
- Die Polynomdivision läuft nach einem schrittweisen Schema ab. Die Terme des Dividenden werden nacheinander geteilt, mit dem Divisor multipliziert und wieder subtrahiert, bis der Wert $0$ oder ein Rest übrig bleibt, durch den nicht weiter geteilt werden kann.
Häufig gestellte Fragen zum Thema Polynomdivision
Transkript Polynomdivision – Erklärung
Kennst du das? Der Berg an Aufgaben ist so groß und unhandlich, dass man gar nicht weiß, wo man anfangen soll. Das einzige was da hilft: Strukturiert ran gehen und das Ganze in viele kleine Häppchen unterteilen. Und DAS ist auch die Grundidee der "Polynomdivision"! Denn wenn wir ein Polynom wie zum Beispiel DIESES hier haben, also die Summe von Vielfachen von Potenzen einer Variable (meistens x), kann es aus verschiedenen Gründen sinnvoll sein, es in mehrere kleinere Polynome zu zerlegen. Dabei hilft uns die Polynomdivision. Aber was heißt das jetzt genau – "Polynomdivision"? Nichts anderes, als dass wir ein Polynom durch ein anderes teilen. Wir fangen erstmal mit einem etwas einfacheren Fall an und betrachten DIESE Rechnung. Wir möchten ein Polynom Dritten Grades durch ein Polynom ERSTEN Grades teilen. Eine wichtige Grundbedingung für die Polynomdivision ist somit erfüllt. Der Grad des Polynoms, durch das wir teilen, darf nämlich nicht größer sein als der Grad des Polynoms, das geteilt wird. Auch wenn die Aufgabe erstmal etwas kompliziert wirkt, ist es gar nicht so schwer. Das Ganze funktioniert nämlich im Prinzip genauso, wie die schriftliche Division, die du bereits gelernt hast. Also gut, dann legen wir mal los. Die Vorgehensweise besteht aus drei grundlegenden Rechenschritten. Als erstes teilen wir die Potenz mit dem größten Exponenten von DIESEM Polynom durch die Potenz mit dem größten Exponenten von DIESEM Polynom. "x hoch drei" geteilt durch "x" ist "x hoch zwei". Und das war dann schon der erste Schritt! Zweitens müssen wir jetzt "zurück multiplizieren". Das heißt: Wir multiplizieren das Ergebnis aus unserem ersten Schritt mit jedem Summanden des hinteren Polynoms. Also nicht nur mit dem x, sondern auch mit der drei. Die Ergebnisse sortieren wir (ihren Exponenten entsprechend) unter das vordere Polynom. Und dann ist auch schon alles für den dritten Schritt vorbereitet. Denn der besteht einfach nur darin, dass wir das so zustande gekommene Polynom von dem oberen Polynom SUBTRAHIEREN. "x hoch drei" fällt dadurch weg, HIER müssen wir darauf achten, dass sich das Vorzeichen durch das Minus vor der Klammer umdreht, (dann bleibt "drei x Quadrat" übrig) und den hinteren Teil des Polynoms können wir einfach übernehmen. Dann geht das Spiel von vorne los! Erstens "dividieren", zweitens: "zurück multiplizieren" und drittens "subtrahieren". Dabei fällt der vordere Summand immer weg, ansonsten haben wir etwas falsch gemacht. Jetzt haben wir es fast geschafft. Einmal noch das Ganze! Dividieren, multiplizieren und subtrahieren. Es geht genau auf, fertig! Dass kein Rest bleibt, ist schonmal ein super Zeichen! Aber um ganz auf Nummer sicher zu gehen, machen wir auch nochmal die Probe. Dafür müssen wir einfach nur unser Ergebnis wieder mit dem Polynom multiplizieren, durch das wir geteilt haben. Und wenn wir das Schritt für Schritt ausrechnen, kommen wir tatsächlich wieder auf unser ursprüngliches Polynom! Einwandfrei! Dann jetzt nochmal zu unserem Polynom vom Anfang! Auch das kriegen wir noch auseinanderdividiert! Wir teilen es mal durch das Polynom "x Quadrat minus vier". Warum? Nun, weil wir es können! Bevor wir loslegen, sollten wir uns aber einmal kurz die Mühe machen, hier ein bisschen Ordnung reinzubringen, indem wir die Summanden nach der Größe der Exponenten sortieren. Denn dann können wir wieder nach dem gleichen Schema vorgehen. Wir dividieren die höchsten Potenzen der Polynome und multiplizieren das Ergebnis mit beiden Summanden des Polynoms, durch das wir teilen. An dieser Stelle aufgepasst! Wir müssen die "minus vier x hoch zwei" an der richtigen Stelle notieren, in diesem Fall also eine Lücke lassen. Dann geht es aber weiter wie gehabt und wir subtrahieren, wobei wir natürlich nicht vergessen dürfen auch die "minus vier x hoch drei" von oben mit runterzuziehen. Dann geht der Algorithmus wieder von vorne los: Dabei solltest du darauf achten, mit den Vorzeichen nicht durcheinander zu kommen. Ein weiterer Durchgang beschert uns dann DIESES Überbleibsel. Jetzt müssen wir kurz innehalten und einen Gang zurück schalten. Ganz am Anfang hatten wir ja schon festgehalten, dass wir die Polynomdivision nur so lange durchführen können, wie der Grad des Polynoms, durch das wir teilen, nicht größer ist als der des Polynoms, das geteilt wird. Das ist jetzt aber der Fall, weshalb wir ans Ende unserer Polynomdivision gekommen sind. Das übrig gebliebene Polynom ist unser Rest. Bleibt nur noch die Frage, wie wir diesen Rest in unser Ergebnis übernehmen. Den müssen wir schließlich auch noch durch "x Quadrat minus vier teilen". Nun, dafür gibt es eine ganz simple Lösung: Wir schreiben den entsprechenden Bruch einfach hinten dran. Wer jetzt ganz genau hinschaut, sieht vielleicht noch, dass wir "x minus 2" sowohl im Zähler als auch im Nenner ausklammern und anschließend kürzen können. Uff, das war ein Brocken! Wir fassen nochmal zusammen, was du dir zur "Polynomdivision" alles merken solltest. Von einer "Polynomdivision" ist die Rede, wenn wir ein Polynom durch ein weiteres Polynom (dessen Grad im Normalfall kleiner ist) teilen. Die Vorgehensweise ist dabei immer gleich und erinnert stark an die schriftliche Division aus früheren Zeiten. Erst dividieren wir die beiden Potenzen mit dem jeweils höchsten Grad, dann wird zurück multipliziert und anschließend subtrahiert. Dieser Algorithmus wird solange durchexerziert, bis wir auch das hartnäckigste Polynom gebrochen und notfalls auch den Rest noch als Bruch in unser Ergebnis übernommen haben. Zugegeben: Wir haben jetzt erstmal nur geklärt, WIE eine Polynomdivision funktioniert, nicht WOZU sie gut sein kann. Sie kann zum Beispiel bei gebrochenrationalen Funktionen, bei der Bestimmung von Nullstellen und auch bei der Linearfaktorzerlegung im Allgemeinen zum Einsatz kommen. Solch interessant klingenden Themen widmen wir uns aber ein andermal, und begnügen uns zunächst mit der Gewissheit, dass wir mit der Polynomdivision zur Not auch die dicksten Brocken aus dem Weg geräumt bekommen.
Polynomdivision – Erklärung Übung
-
Vervollständige die Polynomdivision.
TippsDas Vorgehen bei der Polynomdivision entspricht dem Vorgehen bei der schriftlichen Division ganzer Zahlen.
Nachdem der erste Summand des Ergebnisses ermittelt worden ist, muss dieser mit dem Divisor verrechnet werden. Dieser Term wird dann vom Dividenden abgezogen.
LösungWir betrachten die Polynomdivision $\left(x^3+6x^2-x-30\right):(x+3)$ Schritt für Schritt:
1. Zuerst wird der erste Summand $x^3$ des Dividenden durch den ersten Summanden des Divisors $x$ geteilt:
$\frac{x^3}{x}=x^2$
2. Dieses Ergebnis wird hinter dem Gleichheitszeichen aufgeschrieben.
3. Nun wird das Ergebnis $x^2$ mit dem Divisor $x+3$ multipliziert zu $x^3+3x^2$.
4. Das Produkt wird vom Dividenden subtrahiert:
$x^3+6x^2-x-30-\left(x^3+3x^2\right)=3x^2-x-30$
Dies ist der „neue“ Dividend.
5. Es geht weiter wie in Schritt 1:
$\frac{3x^2}{x}=3x$
Dieses Ergebnis wird hinter $x^2$ auf der rechten Seite des Gleichheitszeichens aufgeschrieben.
6. Wieder wird das Ergebnis mit dem Divisor multipliziert:
$3x\cdot (x+3)=3x^2+9x$
7. Das Produkt wird vom Dividenden subtrahiert:
$3x^2-x-30-\left(3x^2+9x\right)=-10x-30$
8. Erneut geht es weiter wie in Schritt 1:
$\frac{-10x}{x}=-10$
Dieses Ergebnis wird hinter $3x$ auf der rechten Seite des Gleichheitszeichens aufgeschrieben.
9. Das Ergebnis wird mit dem Divisor multipliziert:
$-10\cdot (x+3)=-10x-30$
10. Schließlich wird das Produkt von dem Dividenden subtrahiert:
$-10x-30-(-10x-30)=0$
Damit ergibt sich:
$\left(x^3+6x^2-x-30\right):(x+3) = x^2+3x-10$
-
Gib an, was bei der Polynomdivision zu beachten ist.
TippsEs sind zwei Aussagen richtig.
Für eine Division gilt allgemein:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
LösungBei der Polynomdivision wird ein Polynom durch ein anderes geteilt. Ein Polynom kann dadurch in mehrere kleinere Polynome zerlegt werden. Das Vorgehen entspricht im Allgemeinen dem Vorgehen bei der schriftliche Division ganzer Zahlen.
Wir betrachten die einzelnen Aussagen:
- Der Grad des Polynoms des Divisors darf nicht größer sein als der Grad des Polynoms des Dividenden.
- Es darf kein Rest bleiben: Die letzte Zeile ergibt null.
- Beim Dividenden müssen zu Beginn die Summanden nach der Größe der Exponenten sortiert werden.
- Bei der Probe wird das Ergebnis mit dem Dividenden multipliziert.
-
Bestimme das Ergebnis der Polynomdivision.
TippsAchte auf korrekte Vorzeichen.
Beim dritten Beispiel bleibt ein Rest.
LösungWir gehen bei der Polynomdivision nach dem Schema „dividieren – multiplizieren – subtrahieren“ vor. In den einzelnen Beispielen ergibt sich:
Beispiel 1:
$~~~ (x^{3} +x^{2} +8x-28)~:~(x-2) ~=~x^{2} + 3x+14$
$\underline{-(x^{3}-2x^{2})}$
$~~~~~~~~~~~~~\,3x^{2}+8x-28$
$\quad \quad ~ \underline{-(3x^{2}-6x) }$
$\qquad \qquad \quad ~~ 14x-28$
$\qquad \quad \quad ~~ \underline{-(14x-28)}$
$\qquad \qquad \qquad \quad \quad ~~~~0$
Beispiel 2:
$~~~ (6x^{3} - 3x^{2} \qquad ~ + 9)~:~(x + 1)~=~6x^{2} - 9x + 9$
$\underline{- (6x^{3} + 6x^{2})}$
$~~~~~~~~~~~~~~~ \,9x^{2} \qquad ~ + 9$
$\qquad~~~ \underline{- (9x^{2} - 9x) }$
$\qquad \qquad \qquad ~~ \,9x + 9$
$\qquad \qquad \quad ~~\underline{- (9x - 9)}$
$\qquad \qquad \qquad \qquad ~~ ~~0$
Beispiel 3:
$~~~ (12x^{3}+5x^2 ~~~~~~~~~~~~~~ -~10)~:~(x-2)~=~12x^2 + 29x + 58 ~~~ \left(+~\frac{106}{x-2} ~~\text{Rest}\right)$
$\underline{-(12x^{3}-24x^2) }$
$~~~~~~~~~~~~~~~~~ \,29x^2 ~~ ~~~~~~~~~~-~10$
$\qquad ~~~~~ \underline{-(29x^2-58x) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~-58x~ - ~10$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(58x - 116) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+~106$
-
Berechne das Ergebnis der Polynomdivision.
TippsVergiss die Vorzeichen der Zahlen nicht!
Im Dividenden kommt kein $x^2$ vor, aber im Ergebnis schon.
Mache die Probe, falls du unsicher bist.
Lösung$~~~ (2x^{4}+4x^3 ~~~~~~~~~~~~~ -~~x~~ - ~6)~:~(x+3)~=~2x^3 - 2x^2 + 6x + 19 ~~~ \left(-~\frac{63}{x+3} ~~\text{Rest}\right)$
$\underline{-(2x^4+6x^3) }$
$~~~~~~~~~~~ \,-~2x^3 ~~~~~~~~~~~-~~x ~~~ -~6$
$\qquad \underline{-(-~2x^3-6x^2) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~6x^2 - ~~x ~~~- ~6$
$~~~~~~~~~~~~~~~~~~~~~~~\underline{-(~6x^2+18x)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-~19x~- ~6$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(19x+57)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-63$
-
Gib zu jeder Polynomdivision die passende Probe an.
TippsBei der Probe multiplizierst du das Ergebnis der Polynomdivision mit dem Divisor. Dieses Produkt muss gleich dem Dividenden sein.
Für eine Division gilt allgemein:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
Beispiel:
$\underbrace{48}_{\text{Dividend}} : \underbrace{6}_{\text{Divisor}} = \underbrace{8}_{\text{Ergebnis}}$
Wir machen folgende Probe:
$\underbrace{8}_{\text{Ergebnis}} \cdot \underbrace{6}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden – in diesem Fall $48$.
LösungDas Vorgehen bei der Polynomdivision entspricht dem Vorgehen bei der schriftliche Division. Du musst dich also nur an das nachfolgende Schema halten, um auf die richtige Lösung zu kommen:
$\text{Dividend} : \text{Divisor} = \text{Quotient}$
Nichtsdestotrotz kann es passieren, dass sich Fehler einschleichen. Um zu überprüfen, ob du richtig gerechnet hast, kannst du die Probe machen. Dazu multiplizierst du das Ergebnis der Polynomdivision mit dem Divisor. Dieses Produkt muss gleich dem Dividenden sein. Dann hast du alles richtig gemacht.
Erste Rechnung:
$\underbrace{(5x^3-17x^2+4x+6)}_{\text{Dividend}} : \underbrace{(x-3)}_{\text{Divisor}} = \underbrace{5x^2-2x-2}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{5x^2-2x-2}_{\text{Quotient}} \cdot \underbrace{(x-3)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $5x^3-17x^2+4x+6$.
Zweite Rechnung:
$\underbrace{(4x^3-5x^2-4x-4)}_{\text{Dividend}} : \underbrace{(x-2)}_{\text{Divisor}} = \underbrace{4x^2+3x+2}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{4x^2+3x+2}_{\text{Quotient}} \cdot \underbrace{(x-2)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $4x^3-5x^2-4x-4$.
Dritte Rechnung:
$\underbrace{(x^3-2x^2-8x+21)}_{\text{Dividend}} : \underbrace{(x+3)}_{\text{Divisor}} = \underbrace{x^2-5x+7}_{\text{Quotient}}$
Wir machen folgende Probe:
$\underbrace{5x^2-2x-2}_{\text{Quotient}} \cdot \underbrace{(x+3)}_{\text{Divisor}}$
Dieses Produkt ist dann gleich dem Dividenden, also $x^3-2x^2-8x+21$.
-
Überprüfe die Rechnungen.
TippsAuch wenn eine Polynomdivision keinen Rest hat, kann sie einen Fehler enthalten.
Nur eine der vier Rechnungen ist korrekt.
LösungBei der Polynomdivision gibt es einige häufig auftauchende Fehler, die wir vermeiden wollen:
- Vorzeichenfehler
- Fehler in den Potenzen
- Divisor wird nicht korrekt multipliziert
Wir überprüfen nun die gegebenen Beispiele:
Beispiel 1:
$~~~ (10x^{3} + ~~~~ x^{2} + 9)~:~(\color{#FF66FF}{x}$$ + 1)~=~10x^2 - \color{#FF66FF}{9}$
$\underline{- (10x^{3} + 10x^{2})}$
$~~~~~~~~~~~~~~~ \,-9x^{2} + 9$
$\qquad~~~ \color{#FF66FF}{\underline{- (-9x^2 - 9)}}$
$\qquad \qquad \qquad ~~ \,0$
Bei diesem Beispiel wurden beim Multiplizieren die Potenzen falsch notiert. Korrekt lautet die Polynomdivision:
$~~~ (10x^{3}+ ~~~~ x^2 ~~~~~~~~~~~ +9)~:~(x+1)~=~10x^2 - 9x + 9$
$\underline{-(10x^{3}+10x^2)}$
$~~~~~~~~~~~~~~~~~ \,-9x^2 ~~ ~~~~~~~~+9$
$\qquad ~~~~~ \underline{-(-9x^2-9x) }$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~9x ~+ 9$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~\underline{-(9x+9)}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0$
Beispiel 2:
$~~~ (x^{3} -5x^{2} ~~~~~+16x-30)~:~(x\color{#FF66FF}{-}$ $3) ~=~x^{2} \color{#FF66FF}{-}$ $ 2x+22 ~~~ \left(+~\frac{66}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2})} $
$~~~~~~~~~~~~~~\,-2x^{2}+16x-30$
$\quad \quad ~~ \color{#FF66FF}{\underline{-(-2x^{2}-6x) }}$
$\qquad \qquad \qquad ~~~~22x-30$
$\qquad \quad \quad ~~~~~~~ \underline{-(22x-66)}$
$\qquad \qquad \qquad \quad \quad ~~~~+66$
Hier gibt es einen Vorzeichenfehler. Korrekt lautet die Polynomdivision:
$~~~ (x^{3} -5x^{2} ~~~~~+16x-30)~:~(x-3) ~=~x^{2} - 2x+10$
$\underline{-(x^{3}-3x^{2}) }$
$~~~~~~~~~~~~~~\,-2x^{2}+16x-30$
$\quad \quad ~~ \underline{-(-2x^{2}+6x)}$
$\qquad \qquad \qquad ~~~~10x-30$
$\qquad \quad \quad ~~~~~~~ \underline{-(10x-30)}$
$\qquad \qquad \qquad \quad \quad ~~~~~~~~0$
Beispiel 3:
$~~~ (2x^{3} + 6x^{2} ~~-7x + 4)~:~(x+4) ~=~2x^{2} - 2x+1$
$\underline{-(2x^{3}+8x^{2}) }$
$~~~~~~~~~~~~~~\,-2x^{2}-7x+4$
$\quad \quad ~~ \underline{-(-2x^{2}-8x)}$
$\qquad \qquad \qquad ~~~~~~~x+4 $
$\qquad \quad \quad ~~~~~~~~~~ \underline{-(x+4)}$
$\qquad \qquad \qquad \quad \quad ~~~~~~0$
Dieses Beispiel enthält keinen Fehler.
Beispiel 4:
$~~~ (x^{3} +x^{2} ~~~+8x-10)~:~(x-3) ~=~x^{2} + 4x-4 ~~~ \left(-~\frac{22}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2}) }$
$~~~~~~~~~~~~~~\,4x^{2}+8x-10$
$\quad \quad ~~ \underline{-(4x^{2}-12x)}$
$\qquad \qquad \qquad \color{#FF66FF}{-4x}$$-10$
$\qquad \quad \quad ~~~ \underline{-(-4x+12)}$
$\qquad \qquad \qquad \quad \quad ~~-22$
Hier ist die Subtraktion falsch. Korrekt lautet die Polynomdivision:
$~~~ (x^{3} +x^{2} ~~~+8x-10)~:~(x-3) ~=~x^{2} + 4x+20 ~~~ \left(+~\frac{50}{x-3} ~~\text{Rest}\right)$
$\underline{-(x^{3}-3x^{2})}$
$~~~~~~~~~~~~~~\,4x^{2}+8x-10$
$\quad \quad ~~ \underline{-(4x^{2}-12x)}$
$\qquad \qquad \qquad 20x-10$
$\qquad \quad \quad ~~~ \underline{-(20x-60)}$
$\qquad \qquad \qquad \quad \quad ~~~~50$
9.869
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?