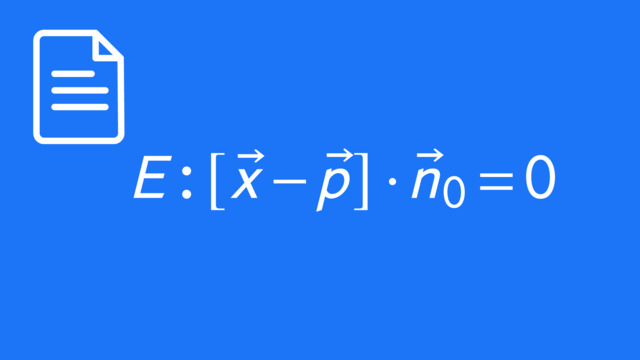Koordinatenform einer Ebene

Koordinatenform einer Ebene Übung

• Beschreibe die Koordinatenform einer Ebene.

  Tipps

  Die allgemeine Ebenengleichung in Normalenform lautet:

  $E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.

  Bei einer Punktprobe wird überprüft, ob ein bestimmter Punkt in der Ebene liegt oder nicht.

  Lösung

  Die Koordinatengleichung ist eine sehr kompakte Darstellungsform der Ebene. Durch sie ist die Ebene eindeutig definiert. Allgemein sieht die Koordinatenform einer Ebene wie folgt aus:

  $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  Wir können erkennen, dass die Koordinatenform ohne Vektoren auskommt.

  Wir vergleichen die Koordinatenform mit der Normalenform:

  • Koordinatenform: $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$
  • Normalenform: $E$: $(\vec{x} - \vec{p}) \cdot \vec{n}=0$

  Auf der linken Seite der Koordinatenform stehen die Koordinaten von dem Normalenvektor:

  $a=n_1 \quad b=n_2 \quad c=n_3$

  Auf der rechten Seite steht das Skalarprodukt von Stützvektor $\vec{p}$ und Normalenvektor $\vec{n}$:

  $d= \vec{p} \cdot \vec{n}$

  Mithilfe der Koordinatenform lassen sich beispielsweise Achsenschnittpunkte und Punktproben einfach berechnen.

• Gib an, wie man die Parameterform in die Koordinatenform umwandelt.

  Tipps

  Führe die Umwandlung an einem Beispiel durch. Dadurch kannst du dir die einzelnen Schritte vergegenwärtigen.

  Du kannst den Normalenvektor, welchen du für die Normalenform brauchst, über das Vektorprodukt der beiden Richtungsvektoren der Parameterform bestimmen.

  Wenn du die Normalenform der Ebene aufgestellt hast, dann kannst du danach die linke Seite dieser Gleichung mithilfe des Skalarproduktes ausmultiplizieren.

  Lösung

  Eine Ebene können wir angeben in:

  1. Parameterform:

  Die allgemeine Ebenengleichung in Parameterform lautet:

  $E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{u}$ und $\vec{v}$ stellen die Richtungsvektoren dar.

  2. Normalenform:

  Die allgemeine Ebenengleichung in Normalenform lautet:

  $E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.

  3. Koordinatenform:

  Die Koordinatenform kommt ohne Vektoren aus. Sie sieht allgemein wie folgt aus:

  $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  
  

  Um die Gleichung einer Ebene in Parameterform in die Koordinatenform umzuwandeln, wandeln wir sie erst in die Normalenform um und diese dann in die Koordinatenform.

  Wir betrachten das Vorgehen an einem Beispiel:

  $E$: $\vec{x} = \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 2 \\ -3 \end{pmatrix} \qquad(r, s \in \mathbb{R})$

  Schritt 1: Normalenvektor bestimmen

  Wir können den Normalenvektor über das Vektorprodukt der beiden Richtungsvektoren bestimmen:

  $\vec{n} = \vec{u} \times \vec{v} = \begin{pmatrix} u_2v_3 - u_3v_2 \\ u_3v_1 - u_1v_3 \\ u_1v_2 - u_2v_1 \end{pmatrix} = \begin{pmatrix}-6-2 \\ 0+9 \\ 6-0 \end{pmatrix} = \begin{pmatrix} -8 \\ 9 \\ 6 \end{pmatrix}$

  Schritt 2: Normalenform der Ebene aufstellen

  Wir verwenden den Stützvektor der Parameterform und den eben berechneten Normalenvektor und ermitteln:

  $E$: $\left( \vec{x} - \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \right) \cdot \begin{pmatrix} -8 \\ 9 \\ 6 \end{pmatrix} = 0$

  Schritt 3: Linke Seite der Gleichung ausmultiplizieren

  Dazu verwenden wir das Skalarprodukt. Wir erhalten im Beispiel:

  $-8x + 9y +6z - (-16 + 0 -6) = 0$

  Schritt 4: Gleichung umstellen

  Um die Gleichung in Koordinatenform zu ermitteln, rechnen wir zunächst die Klammer aus:

  $-8x + 9y +6z - 22=0$

  Wir bringen das Ergebnis auf die rechte Seite und erhalten die Ebenengleichung in Koordinatenform:

  $E$: $-8x+9y+6z = 22$

• Leite die Eigenschaften der Ebene aus der Koordinatenform ab.

  Tipps

  Allgemein sieht die Koordinatenform einer Ebene wie folgt aus:

  $E$: $ax+by+cz=d$

  Du kannst die gegebenen Gleichungen durch Äquivalenzumformungen in diese Form bringen.

  $d=0 \quad \Rightarrow \quad$ Die Ebene verläuft durch den Ursprung.

  Lösung

  Allgemein sieht die Koordinatenform einer Ebene wie folgt aus:

  $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  Aus dieser Gleichung lassen sich in Spezialfällen bestimmte Eigenschaften der Ebene direkt ablesen. Es gilt:

  • $a=0 \quad \Rightarrow \quad$ Die Ebene verläuft parallel zur $x$-Achse.
  • $b=0 \quad \Rightarrow \quad$ Die Ebene verläuft parallel zur $y$-Achse.
  • $c=0 \quad \Rightarrow \quad$ Die Ebene verläuft parallel zur $z$-Achse.
  • $d=0 \quad \Rightarrow \quad$ Die Ebene verläuft durch den Ursprung.

  Bei den gegebenen Ebenen sind die Koordinatengleichungen nicht immer wie oben geordnet. Durch Äquivalenzumformungen können wir sie in diese Form bringen und so noch einfacher die Eigenschaften ablesen. Es ergeben sich folgende Zuordnungen:

  Ebenen parallel zur $\boldsymbol{x}$-Achse:

  • $E$: $5y-4+z=0 \quad \Leftrightarrow \quad E$: $5y+z=4$
  • $E$: $-y=z+1\quad \Leftrightarrow \quad E$: $-y-z=1$

  Ebene parallel zur $\boldsymbol{y}$-Achse:

  • $E$: $5x-8z=9$

  Ebenen parallel zur $\boldsymbol{z}$-Achse:

  • $E: x=3y-2\quad \Leftrightarrow \quad E$: $x-3y=-2$
  • $E: 10=x-y\quad \Leftrightarrow \quad E$: $x-y=10$

  Ebenen durch den Ursprung:
  $E: x+y=z\quad \Leftrightarrow \quad E$: $x+y-z=0$

• Ermittle aus der Normalenform die Koordinatenform der Ebene.

  Tipps

  Die allgemeine Ebenengleichung in Normalenform lautet:

  $E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.

  Die Koordinaten des Normalenvektors stehen vor den Variablen $x$, $y$ und $z$ in der Koordinatenform.

  Lösung

  Um die Gleichung einer Ebene aus der Normalenform in die Koordinatenform umzuwandeln, vergegenwärtigen wir uns zunächst noch einmal die beiden Formen:

  1. Normalenform:

  Die allgemeine Ebenengleichung in Normalenform lautet:

  $E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.

  2. Die Koordinatenform:

  Die Koordinatenform kommt ohne Vektoren aus. Sie sieht allgemein wie folgt aus:

  $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  Um die Gleichung einer Ebene in Normalenform in die Koordinatenform umzuwandeln, multiplizieren wir die linke Seite der Normalenform mithilfe des Skalarproduktes aus und vereinfachen dann die erhaltene Gleichung. Allgemein sieht das so aus:

  $E$: $\left( \vec{x} - \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \right) \cdot \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} = 0$

  $n_1x + n_2y + n_3z - (p_1n_1 + p_2n_2 + p_3n_3) =0 \quad \Leftrightarrow \quad n_1x + n_2y + n_3z = p_1n_1 + p_2n_2 + p_3n_3$

  Wir können bereits erkennen, dass vor den Variablen $x$, $y$ und $z$ die Koordinaten des Normalenvektors stehen.

  
  

  Nun betrachten wir die Umwandlung an den konkreten Beispielen:

  Beispiel 1

  $E$: $\left( \vec{x} - \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} \right) \cdot \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix} = 0$

  $\begin{array}{llllll} \Rightarrow 2x& +4y & -2z &-(2+0-8) & = & 0 \\ \Leftrightarrow 2x& +4y & -2z &+6 & = & 0 &| -6\\ \Leftrightarrow 2x& +4y & -2z & & = & -6 \\ \end{array}$

  Beispiel 2

  $E$: $\left( \vec{x} - \begin{pmatrix} 0 \\ 0 \\ -4 \end{pmatrix} \right) \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix} = 0$

  $\begin{array}{llllll} \Rightarrow 2x& & -4z &-(0+0+16) & = & 0 \\ \Leftrightarrow 2x& & -4z &-16 & = & 0 &| +16\\ \Leftrightarrow 2x& & -4z & & = & 16 \\ \end{array}$

  Beispiel 3

  $E$: $\left( \vec{x} - \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix} \right) \cdot \begin{pmatrix} 3 \\ 1 \\ -1 \end{pmatrix} = 0$

  $\begin{array}{llllll} \Rightarrow 3x& +y & -z &-(6+4+2) & = & 0 \\ \Leftrightarrow 3x& +y & -z &-12 & = & 0 &| +12\\ \Leftrightarrow 3x& +y & -z & & = & 12 \\ \end{array}$

  Beispiel 4

  $E$: $\left( \vec{x} - \begin{pmatrix} 1 \\ -5\\ -2 \end{pmatrix} \right) \cdot \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix} = 0$

  $\begin{array}{llllll} \Rightarrow 2x& +4y & -2z &-(2-20+4) & = & 0 \\ \Leftrightarrow 2x& +4y & -2z &+14 & = & 0 &| -14\\ \Leftrightarrow 2x& +4y & -2z & & = & -14 \\ \end{array}$

• Gib an, welche Ebenen in Koordinatenform vorliegen.

  Tipps

  Die Darstellung einer Ebene in Koordinatenform kommt ohne Vektoren aus.

  Beispiel:

  $E$: $x + 5y -3z=13$

  Diese Ebene liegt in Koordinatenform vor.

  Drei der gegebenen Ebenen liegen in Koordinatenform vor.

  Lösung

  Eine Ebene können wir angeben in:

  • Parameterform
  • Normalenform
  • Koordinatenform

  
  

  Parameterform

  Die allgemeine Ebenengleichung in Parameterform lautet:

  $E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{u}$ und $\vec{v}$ stellen die Richtungsvektoren dar.

  
  

  Normalenform

  Die allgemeine Ebenengleichung in Normalenform lautet:

  $E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$

  Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.

  
  

  Koordinatenform

  Die Koordinatenform ist eine etwas andere Darstellung der Ebene und kommt ohne Vektoren aus. Sie sieht allgemein wie folgt aus:

  $E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  
  
  

  Wir betrachten die gegebenen Ebenen:

  
  

  $E$: $\vec{x} = \begin{pmatrix} 4 \\ 0 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ -6 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 2 \\ -3 \end{pmatrix} \qquad(r, s \in \mathbb{R})$

  Diese Ebene liegt in Parameterform und nicht in Koordinatenform vor.

  
  

  $E$: $\left( \vec{x} - \begin{pmatrix} -7 \\ 2 \\ -1 \end{pmatrix} \right) \cdot \begin{pmatrix} -1 \\ 0 \\ 6 \end{pmatrix} = 0$

  Diese Ebene liegt in Normalenform und nicht in Koordinatenform vor.

  
  

  $E$: $3x + 2y -z=9$

  Diese Ebene liegt in Koordinatenform vor.

  
  

  $E$: $y -z=9$

  Auch wenn in dieser Gleichung die Variable $x$ nicht vorkommt, liegt diese Ebene in Koordinatenform vor. Der Koeffizient vor der Variable $x$ ist $0$.

  
  

  $E$: $\left( \vec{x} - \begin{pmatrix} -1 \\ 0 \\ 2 \end{pmatrix} \right) \cdot \begin{pmatrix} -1 \\ 3 \\ 3 \end{pmatrix} = 0$

  Diese Ebene liegt in Normalenform und nicht in Koordinatenform vor.

  
  

  $E$: $4x - 2y + 4=0$

  Diese Ebene liegt in Koordinatenform vor.

• Berechne die fehlenden Koordinaten.

  Tipps

  Setze den Punkt in die Koordinatenform der Ebene ein und ergänze die fehlende Koordinate so, dass die Gleichung erfüllt ist.

  Beispiel:

  $E$: $2x - 3y + 2z = 2\qquad P(1 | {-}3 | n)$

  Wir setzen ein:

  $\begin{array}{lllll} 2 \cdot 1& - 3 \cdot (-3) & + 2 \cdot n & = & 13\\ 2 & + 9 & + 2 \cdot n &= & 13 \\ 11 & & + 2 \cdot n& = & 13 \end{array}$

  Hier können wir direkt erkennen, dass $n=1$ sein muss, damit die Gleichung erfüllt ist. Der Punkt lautet also $P(1|{-}3|1)$.

  Lösung

  Mithilfe der Koordinatenform einer Ebene können wir mit der Punktprobe ermitteln, ob ein Punkt auf einer Ebene liegt oder nicht:

  $E: ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$

  Dazu setzen wir die Koordinaten des gegebenen Punktes für $x$, $y$ und $z$ ein und überprüfen, ob die Gleichung erfüllt ist ($\Rightarrow$ Punkt liegt auf der Ebene) oder nicht ($\Rightarrow$ Punkt liegt nicht auf der Ebene).

  Andersherum können wir so auch die fehlende Koordinate eines auf der Ebene liegenden Punktes ermitteln. Dazu setzen wir den Punkt wieder in die Koordinatenform ein und ergänzen die fehlende Koordinate so, dass die Gleichung erfüllt ist.

  
  

  Wir betrachten die gegebenen Beispiele und nennen die fehlende Koordinate dabei $n$:

  Beispiel 1

  $E$: $3x - 2y + z = 12\qquad P(2 | 1 | n)$

  Wir setzen ein:

  $\begin{array}{lllll} 3 \cdot 2& - 2 \cdot 1 & +~n & = & 12\\ 6 & -2 & +~n &= & 12 \\ 4 & & +~n& = & 12 \end{array}$

  Hier können wir direkt erkennen, dass $n=8$ sein muss, damit die Gleichung erfüllt ist. Der Punkt lautet also $P(2|1|8)$.

  Beispiel 2

  $E$: $-2x + 2z = -6\qquad P(n | {-}7 | {-}2)$

  Wir setzen ein:

  $\begin{array}{lllll} -2 \cdot n& & + 2 \cdot (-2) & = & -6\\ -2 \cdot n & & -4 &= & -6 & |+4\\ -2 \cdot n & & &= &-2 & |: (-2)\\ n & & &= & 1 \end{array}$

  Durch Umstellen der Gleichung erhalten wir $n=1$. Der Punkt lautet also $P(1|{-}7|{-}2)$.

  Beispiel 3

  $E$: $-x + 4y - 3z = 10 \qquad P(2 | n | {-}4)$

  Wir setzen ein:

  $\begin{array}{lllll} -2 & +4 \cdot n & -3 \cdot (-4) & = & 10\\ -2 & +4 \cdot n & +12 & = & 10\\ & 4 \cdot n &+10 & = & 10 & |-10\\ & 4 \cdot n & & = & 0 &|:4\\ &n & &= & 0 \end{array}$

  Durch Umstellen der Gleichung erhalten wir $n=0$. Der Punkt lautet also $P(2|0|{-}4)$.