Integralrechnung – Fläche zwischen zwei Graphen

Integralrechnung – Fläche zwischen zwei Graphen Übung

• Beschreibe, wie man die Fläche zwischen zwei Funktionsgraphen berechnen kann.

  Tipps

  Die Nullstellen der Differenzfunktion entsprechen den Schnittstellen der beiden Funktionsgraphen.

  Mithilfe der Schnittstellen der beiden Funktionsgraphen, kannst du die Fläche in mehrere Teile unterteilen. Für jede Teilfläche musst du ein einzelnes Teilintegral berechnen. In der Abbildung ergeben sich zwei Teilflächen, es müssen in diesem Beispiel also zwei Teilintegrale berechnet werden.

  Lösung

  Ist der Flächeninhalt zwischen zwei Funktionsgraphen gesucht, so müssen wir meist die Intervallgrenzen selbst bestimmen. Die Intervallgrenzen entsprechen dann den äußeren Schnittstellen der beiden Graphen.

  Schritt 1:
  Dazu stellen wir zuerst die Differenzfunktion der beiden Funktionen auf. Für die Funktionen $f(x)$ und $g(x)$ lautet die Differenzfunktion $f(x)-g(x)$.

  Schritt 2:
  Anschließend bestimmen wir die Nullstellen der Differenzfunktion. Dazu setzen wir die Differenzfunktion gleich Null: $f(x)-g(x)=0$ und lösen diese Gleichung nach $x$ auf. Die Nullstellen entsprechen den Schnittstellen der Graphen von $f(x)$ und $g(x)$. Diese stellen die Intervallgrenzen der zu berechnenden Integrale dar.

  Schritt 3:
  Wir berechnen nun die Teilintegrale zwischen den Schnittstellen. Je nachdem wie viele Schnittstellen die Funktionsgraphen von $f(x)$ und $g(x)$ haben, müssen wir mehrere Integrale berechnen. Zwischen zwei benachbarten Schnittstellen berechnen wir je ein Integral.

  Schritt 4:
  Zuletzt addieren wir die Beträge der erhaltenen Werte, da Flächeninhalte stets positiv sind. So ergibt sich der Inhalt der gesamten Fläche, welche durch die Graphen der beiden Funktionen eingeschlossen wird.

• Vervollständige die Rechnung zur Bestimmung des Flächeninhalts zwischen den dargestellten Funktionsgraphen.

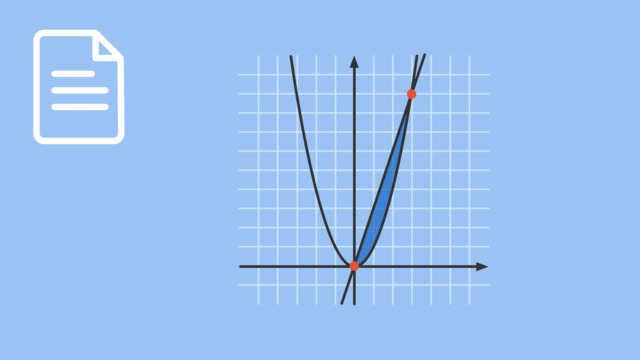
  Tipps

  Hier ist die gesuchte Fläche markiert. Sie besteht aus zwei Teilflächen. Die eine Teilfläche liegt im Intervall $[0; 2]$, die andere Teilfläche liegt im Intervall $[2; 3]$.

  Für die Bestimmung der Nullstellen hilft dir folgender Merksatz:

  Ein Produkt ist genau dann Null, wenn einer der beiden Faktoren Null ist.

  Lösung

  Die beiden abgebildeten Graphen von $f$ und $g$ schließen zwei Teilflächen ein. Um den Flächeninhalt zwischen den beiden Funktionsgraphen zu bestimmen, bilden wir zuerst die Differenzfunktion der beiden Funktionen:

  $f(x)-g(x) = x^3-5x^2+7x-2 - (x-2) = x^3-5x^2+7x-2 - x+2 = x^3-5x^2+6x $

  Die Nullstellen der Differenzfunktion entsprechen den Schnittstellen der Graphen von $f$ und $g$. Wir bestimmen die Nullstellen der Differenzfunktion über die Gleichung:

  $x^3-5x^2+6x=0$

  Wir können die erste Nullstelle bestimmen, indem wir $x$ ausklammern:

  $x \cdot (x^2-5x+6) = 0 \quad \Rightarrow \quad x_1=0$

  Die weiteren Nullstellen können wir berechnen, indem wir die Klammer gleich Null setzen und die $pq$-Formel anwenden. Es ergibt sich:

  $x^2-5x+6= 0 \quad \Leftrightarrow \quad x_2=2$ und $x_3=3$

  Wir benötigen zwei Teilintegrale zwischen je zwei Schnittstellen: Die eine Fläche wird im Bereich zwischen $x=0$ und $x=2$ eingeschlossen, und die andere Fläche zwischen $x=2$ und $x=3$.

  $\displaystyle \int\limits_{0}^{2} x^3-5x^2+6x~\text{d}x = \left[ \frac{1}{4}x^4-\frac{5}{3}x^3+3x^2 \right]_{0}^{2} $

  $= \left(\dfrac{1}{4} \cdot 2^4-\dfrac{5}{3} \cdot 2^3+3 \cdot 2^2\right) - \left(\dfrac{1}{4} \cdot 0^4-\dfrac{5}{3} \cdot 0^3+3 \cdot 0^2\right) = \dfrac{8}{3}$

  $\displaystyle \int\limits_{2}^{3} x^3-5x^2+6x~\text{d}x = \left[ \frac{1}{4}x^4-\frac{5}{3}x^3+3x^2 \right]_{2}^{3} $

  $= \left(\dfrac{1}{4} \cdot 3^4-\dfrac{5}{3} \cdot 3^3+3 \cdot 3^2\right) - \left(\dfrac{1}{4} \cdot 2^4-\dfrac{5}{3} \cdot 2^3+3 \cdot 2^2\right) = -\dfrac{5}{12}$

  Um den gesamten eingeschlossenen Flächeninhalt zu ermitteln, addieren wir die Beträge der erhaltenen Werte:

  $\displaystyle A= \left|\frac{8}{3}\right| +\left|-\frac{5}{12}\right| = \frac{37}{12}$

• Überprüfe die Aussagen zur Bestimmung des Flächeninhaltes zwischen zwei Funktionsgraphen.

  Tipps

  Die Anzahl der Nullstellen der Differenzfunktion entspricht der Anzahl der Schnittstellen der Funktionsgraphen.

  Eine Funktion $3.$ Grades hat maximal drei Nullstellen.

  Lösung

  Wir überprüfen die Aussagen, indem wir uns noch einmal den Lösungsweg zur Bestimmung des Flächeninhaltes zwischen zwei Funktionsgraphen vergegenwärtigen:

  Schritt 1:
  Wir bilden zuerst die Differenzfunktion der beiden Funktionen: $f(x)-g(x)$

  Schritt 2:
  Die Nullstellen der Differenzfunktion entsprechen den Schnittstellen der Funktionsgraphen von $f$ und $g$. Wir berechnen sie, indem wir die Differenzfunktion gleich Null setzen: $f(x) - g(x)$.
  Alternativ können wir die Funktionsterme von $f$ und $g$ auch gleich setzen: $f(x)=g(x)$.

  Die Aussage "Die Schnittstellen der Graphen können durch Gleichsetzen der Funktionsterme ermittelt werden." ist also richtig.

  Schritt 3:
  Wir berechnen dann die Teilintegrale zwischen den Schnittstellen. Zwischen zwei benachbarten Schnittstellen berechnen wir je ein Integral. Zwischen drei Schnittstellen liegen demnach zwei Teilflächen, also zwei Teilintegrale. Zwischen vier Schnittstellen liegen drei Teilflächen usw. Die Anzahl der Teilintegrale ist also immer um eins niedriger, als die Anzahl der Schnittstellen.

  Da die Anzahl der Schnittstellen der Graphen gleich der Anzahl der Nullstellen der Differenzfunktion ist, ist die Aussage "Die Anzahl der zu bestimmenden Teilintegrale entspricht der Anzahl der Nullstellen der Differenzfunktion." falsch.

  Die Aussage "Die Anzahl der Teilflächen ist durch den Grad der beiden Funktionen begrenzt." ist richtig, da der Grad der Funktionen die maximale Zahl der Nullstellen eines Graphen bestimmt.

  Beim Berechnen der Teilintegrale verwenden wir die Schnittstellen der Graphen als Integrationsgrenzen und bilden die Teilintegrale über die Differenzfunktion.

  Die Aussage "Beim Aufstellen der bestimmten Integrale müssen wir die Differenzfunktion verwenden." ist demnach richtig.

  Bei den Integralen können sich negative Werte ergeben. Dies ist immer dann der Fall, wenn der Graph von $g$ zwischen den Schnittstellen oberhalb des Graphen von $f$ verläuft. Da eine Fläche nie negativ sein kann, bilden wir für jedes Teilintegral den Betrag.

  Schritt 4:
  Um den Flächeninhalt der gesamten Fläche, welche durch die beiden Funktionsgraphen eingeschlossen wird, zu ermitteln, addieren wir die Beträge der Ergebnisse der bestimmten Integrale.

  Die Aussage "Liegt die Fläche, die von zwei Funktionen eingeschlossen wird, unterhalb der $x$-Achse, so hat sie einen negativen Flächeninhalt." ist falsch, da eine Fläche keinen negativen Flächeninhalt haben kann und daher die Beträge, welche stets positiv sind, addiert werden.

• Berechne die Fläche zwischen den beiden Funktionsgraphen in den vorgegebenen Grenzen.

  Tipps

  Bestimme zunächst die Differenzfunktion $f(x)-g(x)$ und überprüfe, dass in dem gegebenen Intervall keine weiteren Nullstellen der Differenzfunktion liegen.

  Bestimme dann das Integral $\displaystyle \int\limits_{a}^{b} f(x)-g(x)~\text{d}x$ in den gegebenen Grenzen $a = x_1$ und $b = x_2$.

  Lösung

  Um die Fläche zwischen zwei Funktionsgraphen zu berechnen, müssen wir zunächst die Differenzfunktion aufstellen:
  $f(x) - g(x)$
  Da in unserem Fall die Integrationsgrenzen bereits gegeben sind, können wir dann direkt das Integral der Differenzfunktion mit den angegebenen Grenzen aufstellen, sofern in dem gegebenen Intervall keine weiteren Nullstellen der Differenzfunktion liegen.
  Somit ergibt sich:

  Aufgabe 1: $f(x)=x^4+x^3+3x-2$ und $g(x)=x^4+x-2$ mit $x_1 =-2$ und $x_2=0$
  Wir berechnen die Differenzfunktion:
  $f(x)-g(x) = x^4+x^3+3x-2 - (x^4+x-2) = x^3+2x = x(x^2+2)$
  Da außer $x=0$ keine Nullstellen vorliegen, berechnen wir das Integral:
  $\displaystyle \int\limits_{-2}^{0} x^3+2x~\text{d}x = \left[ \dfrac{1}{4}x^4 - x^2 \right]_{-2}^{0} = \left(\dfrac{1}{4} \cdot 0^4 - 0^2\right) - \left(\dfrac{1}{4} \cdot (-2)^4 - (-2)^2\right) = 0-8=-8$
  Die eingeschlossene Fläche ist: $A=|-\!8|=8.$

  Aufgabe 2: $f(x)=3x^2-x+8$ und $g(x)=4x^2+6$ mit $x_1 =-2$ und $x_2=1$
  Wir berechnen die Differenzfunktion:
  $f(x)-g(x) = 3x^2-x+8 - (4x^2+6) = -x^2-x+2 $
  Da die beiden gegebenen Grenzen die Nullstellen der Differenzfunktion sind, berechnen wir direkt das Integral:
  $\displaystyle \int\limits_{-2}^{1} -x^2-x+2~\text{d}x = \left[ -\dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 + 2x \right]_{-2}^{1} $

  $= \left(-\dfrac{1}{3} \cdot 1^3 - \dfrac{1}{2} \cdot 1^2 + 2 \cdot 1\right) - \left(-\dfrac{1}{3} \cdot (-2)^3 - \dfrac{1}{2} \cdot (-2)^2 + 2 \cdot (-2)\right) = \dfrac{7}{6} - \left(-\dfrac{10}{3}\right) = 4{,}5$
  Die eingeschlossene Fläche ist: $A=4{,}5$.

  Aufgabe 3: $f(x)=3x^3+6$ und $g(x)=3x^3-2x+2$ mit $x_1 =0$ und $x_2=2$
  Wir berechnen die Differenzfunktion:
  $f(x)-g(x) = 3x^3+6 - (3x^3-2x+2) = 2x+4 $
  Da die Differenzfunktion linear ist und daher nur genau eine Nullstelle hat, nämlich $x=2$, berechnen wir direkt das Integral:
  $\displaystyle \int\limits_{0}^{2} 2x+4~\text{d}x = \left[ x^2 +4x \right]_{0}^{2} =\left(2^2 + 4 \cdot 2\right) - \left(0^2 + 4 \cdot 0\right) = 12-0=12$
  Die eingeschlossene Fläche ist: $A=12.$

  Aufgabe 4: $f(x)=2x^2$ und $g(x)=6x$ mit $x_1 =0$ und $x_2=3$
  Wir berechnen die Differenzfunktion:
  $f(x)-g(x) = 2x^2 - (6x) = 2x^2-6x $
  Da die beiden gegebenen Grenzen die Nullstellen der Differenzfunktion sind, berechnen wir direkt das Integral:
  $\displaystyle \int\limits_{0}^{3} 2x^2-6x~\text{d}x = \left[ \dfrac{2}{3}x^3 - 3x^2 \right]_{0}^{3} = \left(\dfrac{2}{3} \cdot 3^3 - 3 \cdot 3^2\right) - \left(\dfrac{2}{3} \cdot 0^3 - 3 \cdot 0^2\right) = -9-0=-9$
  Die eingeschlossene Fläche ist: $A=|-\!9|=9$.

• Gib an, bei welchen Abbildungen das Integral $~\int\limits_a^b f(x)-g(x)~\text{d}x~~~$einen positiven Wert hat.

  Tipps

  Das Integral $\int\limits_a^b f(x)-g(x)~\text{d}x$ mit den Schnittstellen $a$ und $b$ der beiden Graphen von $f$ und $g$ als Integrationsgrenzen, liefert einen positiven Wert, wenn der Graph von $f$ im Intervall $[a,b]$ oberhalb des Graphen von $g$ verläuft.

  Die markierte Fläche $A$ wird berechnet, indem die Fläche $A_2$ zwischen dem Graphen von $g$ und der $x$-Achse von der Fläche $A_1$ zwischen dem Graphen von $f$ und der $x$-Achse subtrahiert wird.

  Lösung

  Ein bestimmtes Integral $\int\limits_a^b f(x)~\text{d}x$ beschreibt die Fläche, die vom Graphen der Funktion $f$ und der $x$-Achse im Intervall $[a,b]$ eingeschlossen wird. Dabei ergeben sich für Flächen unterhalb der $x$-Achse negative Werte und für Flächen oberhalb der $x$-Achse positive Werte.

  Betrachten wir das Integral $\int\limits_a^b f(x)-g(x)~\text{d}x$ zwischen den beiden Schnittstellen $a$ und $b$ der Funktiongraphen von $f$ und $g$, so ergibt sich ein positiver Wert, wenn der Graph von $f$ im Intervall $[a,b]$ oberhalb des Graphen von $g$ verläuft. Es ergibt sich hingegen ein negativer Wert, wenn der Graph von $f$ in diesem Intervall unterhalb des Graphen von $g$ verläuft.

  Wir betrachten die abgebildeten Graphen und untersuchen das Vorzeichen des bestimmten Integrals ${\int\limits_a^b f(x)-g(x)~\text{d}x}$:

  • Das erste Integral mit der gelben Fläche liefert einen positiven Wert, da der Graph von $f$ im Intervall $[a,b]$ oberhalb des Graphen von $g$ verläuft.
  • Das zweite Integral mit der violetten Fläche liefert einen negativen Wert, da der Graph von $f$ im Intervall $[a,b]$ unterhalb des Graphen von $g$ verläuft.
  • Das dritte Integral mit der roten Fläche liefert einen positiven Wert, da der Graph von $f$ im Intervall $[a,b]$ oberhalb des Graphen von $g$ verläuft.
  • Das vierte Integral mit der grünen Fläche liefert einen negativen Wert, da der Graph von $f$ im Intervall $[a,b]$ unterhalb des Graphen von $g$ verläuft.

  
  

  Hinweis: Da Flächen stets positiv sind, wird der Betrag des Integrals gebildet, um den eingeschlossenen Flächeninhalt zu erhalten.

• Ermittle die Fläche, welche die beiden gegebenen Funktionen einschließen.

  Tipps

  Die Differenzfunktion lautet: $f(x)-g(x) = \dfrac{1}{4}x^3- \dfrac{1}{4}x^2-3x$

  Die Graphen der Funktionen haben drei Schnittstellen:

  $x_1=-3, ~x_2=0, ~x_3=4$

  Hier siehst du die gesuchte Fläche gelb markiert.

  Lösung

  Um den Flächeninhalt zwischen den beiden Funktionsgraphen zu bestimmen, müssen wir die Intervallgrenzen selbst bestimmen. Dazu bilden wir zuerst die Differenzfunktion der beiden Funktionen:

  $\begin{array}{rcl} f(x)-g(x) &=& \dfrac{1}{4}x^3-4x+1 - \left(\dfrac{1}{4}x^2-x+1\right) \\ && \\ &=& \dfrac{1}{4}x^3-4x+1 - \dfrac{1}{4}x^2+x-1 \\ && \\ &=& \dfrac{1}{4}x^3- \dfrac{1}{4}x^2-3x \end{array}$

  Wir berechnen nun die Nullstellen der Differenzfunktion. Dazu setzen wir die Differenzfunktion gleich Null:

  $\dfrac{1}{4}x^3- \dfrac{1}{4}x^2-3x = 0$

  Wir können die erste Nullstelle bestimmen, indem wir $x$ ausklammern:

  $x \left( \dfrac{1}{4}x^2- \dfrac{1}{4}x -3\right) = 0 \Rightarrow x_1=0$

  Die weiteren Nullstellen können wir berechnen, indem wir die Klammer gleich Null setzen und die $pq$-Formel anwenden:

  $\dfrac{1}{4}x^2- \dfrac{1}{4}x -3 = 0 \quad | \cdot 4$
  $\Leftrightarrow x^2-x-12=0$
  $\Rightarrow \quad x_{2,3} = -\dfrac{p}{2} \pm \sqrt{ \left( \dfrac{p}{2} \right)^{2} -q } = \dfrac{1}{2} \pm \sqrt{ \left( \dfrac{1}{2} \right)^{2} +12 } $
  $\Rightarrow \quad x_2=-3$ und $x_3=4$

  Die Nullstellen entsprechen den Schnittstellen der Funktionen $f(x)$ und $g(x)$. Wir berechnen somit zwei Teilintegrale zwischen den Schnittstellen: Die eine Fläche wird im Bereich zwischen $x=-3$ und $x=0$ eingeschlossen und die andere Fläche zwischen $x=0$ und $x=4$. Dies kannst du auch in den abgebildeten Funktionsgraphen erkennen.

  $\displaystyle \int\limits_{-3}^{0} \dfrac{1}{4}x^3- \dfrac{1}{4}x^2-3x~\text{d}x$
  $\begin{array}{rcl} \quad&=& \bigg[ \dfrac{1}{16}x^4- \dfrac{1}{12}x^3-\dfrac{3}{2}x^2 \bigg]_{-3}^{0} \\ && \\ &=& \left(\dfrac{1}{16} \cdot 0^4- \dfrac{1}{12} \cdot 0^3-\dfrac{3}{2} \cdot 0^2\right) - \left(\dfrac{1}{16} \cdot (-3)^4- \dfrac{1}{12} \cdot (-3)^3-\frac{3}{2} \cdot (-3)^2\right) \\ && \\ &=& -\dfrac{99}{16} \end{array}$

  $\displaystyle \int\limits_{0}^{4} \dfrac{1}{4}x^3- \dfrac{1}{4}x^2-3x~\text{d}x$
  $\begin{array}{rcl} \quad &=& \bigg[ \dfrac{1}{16}x^4- \dfrac{1}{12}x^3-\dfrac{3}{2}x^2 \bigg]_{0}^{4} \\ && \\ &=& \left(\dfrac{1}{16} \cdot 4^4- \dfrac{1}{12} \cdot 4^3-\dfrac{3}{2} \cdot 4^2\right) - \left(\dfrac{1}{16} \cdot 0^4- \dfrac{1}{12} \cdot 0^3-\dfrac{3}{2} \cdot 0^2\right) \\ && \\ &=& -\dfrac{40}{3} \end{array}$

  Um den Flächeninhalt der gesamten Fläche, welche durch die beiden Funktionen eingeschlossen wird, zu ermitteln, addieren wir die Beträge der erhaltenen Werte:

  $A= \left|-\dfrac{99}{16}\right| +\left|-\dfrac{40}{3}\right| \approx 19,\!5$