Fläche zwischen Funktionsgraphen mit Integralen berechnen


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Fläche zwischen Funktionsgraphen mit Integralen berechnen
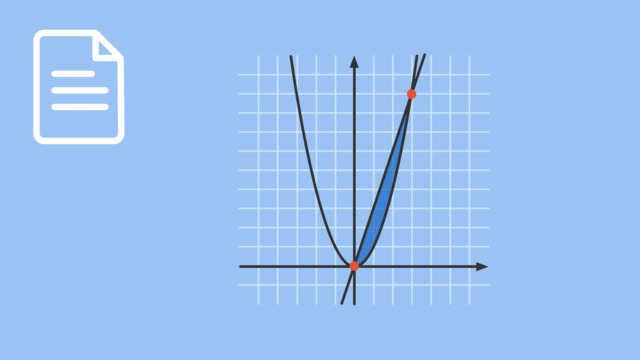
Wie kannst du die Fläche zwischen Funktionsgraphen berechnen? Wie du die Fläche zwischen einem Funktionsgraphen und der x- Achse berechnest, weißt du bereits. Genau dieses Vorwissen wird dir nun weiterhelfen. Bei dem Problem die Fläche zwischen Funktionsgraphen berechnen zu wollen, handelt es sich um eine klassische Anwendung der Integralrechnung. Wir beginnen mit der Problemstellung und zeigen dir an einem Beispiel zwei Methoden mit denen du das Problem lösen kannst. Viel Spaß!
Transkript Fläche zwischen Funktionsgraphen mit Integralen berechnen
Hi. Heute geht es um eine klassische Anwendung der Integralrechnung. Die Berechnung der Fläche zwischen zwei Funktionsgraphen. Wie wir die Fläche zwischen einem Funktionsgraphen und der x-Achse berechnen, wissen wir bereits. Wie du gleich sehen wirst, führen wir die Flächenberechnung zwischen Graphen auf diesen Fall zurück. “Mathematische Probleme auf Bekanntes zurückführen” – das ist eigentlich immer eine gute Strategie. Dazu werden wir zunächst die Problemstellung genauer formulieren. Dann werden wir anhand eines Beispiels eine Berechnung der Fläche zwischen zwei Funktionsgraphen durchführen. 1. Zunächst also die Problemstellung: Worum geht es? Wir betrachten die Graphen zweier Funktionen f und g, die genau zwei Schnittpunkte haben. Der Einfachheit halber nehmen wir zudem an, dass beide Graphen oberhalb der x-Achse liegen. Was uns nun interessiert, ist die Fläche zwischen den beiden Graphen mit Flächeninhalt A. Also vom linken Schnittpunkt bis zum rechten. Kurz: Wir wollen A ausrechnen. Halt, werden einige sagen. Sind das nicht starke Vereinfachungen? Nein. Denn nehmen wir an, f und g hätten mehr als zwei Schnittpunkte, dann würden wir das Problem in mehrere zerlegen. Also eine Fläche nach der anderen berechnen. Erst A1, dann A2 und so weiter. Immer von Schnittpunkt zu Schnittpunkt. Und zum anderen werden wir am Ende sehen, dass wir beide Graphen nach unten schieben können, oder, was dasselbe ist, die x-Achse nach oben, ohne dass das Ergebnis sich verändert. Unsere oben genannte Problemstellung trifft also wirklich den Kern des Problems. Wie gehen wir nun vor bei der Berechnung des gesuchten Flächeninhalts? Zwei Methoden sind prinzipiell möglich: 1. Wir berechnen die Schnittpunkte der Graphen, wobei uns nur deren x-Koordinaten a und b interessieren. Dann bestimmen wir die Fläche mit Flächeninhalt Af unter dem Graphen von f, und die Fläche mit Flächeninhalt Ag unter g, jeweils zwischen a und b. Und schließlich subtrahieren wir: Af-Ag. Diese Differenz ist die Größe, die wir suchen. A=Af-Ag. 2. Wir können aber auch zunächst eine Differenzenfunktion h mit dem Funktionsterm h(x)=f(x)-g(x) bestimmen, deren Nullstellen genau die x-Koordinaten a und b der Schnittpunkte von f und g sind. Der Flächeninhalt Ah der Fläche unter dem Graphen von h, also zwischen h und der x-Achse, ist nun die Größe, die wir suchen. A=Ah. Beide Methoden laufen rechnerisch auf dasselbe hinaus. Das machen wir uns an einem Beispiel deutlich. Gegeben sind die Funktionen f mit f(x)=-x2+6x-3, und g mit g(x)=x2-4x+5. Nach Methode eins rechnen wir zunächst die Schnittpunkte aus. Setzen also f(x)=g(x), das heißt -x2+6x-3=x2-4x+5. Wir bringen die rechte auf die linke Seite und erhalten -2x2+10x-8=0. Und nach Division durch -2: x2+5x-4=0. Dieses quadratische Polynom lässt sich durch die p-q-Formel, oder die Mitternachtsformel lösen. Wir erhalten Nullstellen bei x1=1 und x2=4. Gesucht ist daher die Fläche, die von den Graphen in dem abgeschlossenen Intervall von eins bis vier eingeschlossen wird. Der Graph von f liegt oberhalb des Graphen von g. Also berechnen wir die Differenz Af-Ag=14f(x)dx -14g(x)dx. Beide Integrale können wir zusammenfassen zum 14f(x) - g(x)dx. Also dem 14-2x2 + 10x - 8dx. Die entsprechende Stammfunktion lautet F(x)=-2/3x3+5x2-8x, die wir nun auf dem Intervall zwischen eins und vier auswerten müssen. Wir wenden den Hauptsatz der Differential- und Integralrechnung an und erhalten F(4)-F(1)=(-2/3×43+5×42-8×4)-(-2/3×13+5×122-8×1)=-128/3+80-32+2/3-5+8. Dies ergibt neun. Die Fläche zwischen den Graphen hat also den Flächeninhalt A = 9FE (Flächeneinheiten). Mit der zweiten Methode würden wir zunächst die Differenzfunktion h(x) aus der Differenz der beiden Funktionen f(x) und g(x) berechnen, also h(x)=f(x)-g(x) bestimmen. Dann die Nullstellen dieses Terms bestimmen und ihn auf den entsprechenden Intervall integrieren. Berechnen wir also die Differenzfunktion h(x). h(x)=f(x)-g(x)=-x2+6x-3-(x2-4x+5). Das ergibt: -2x2+10x-8. Merkst du etwas? Das ist ja genau der Term, den wir eben nach der Zusammenfassung der Integrale bei der ersten Methode erhalten haben. Als Nullstellen der Differenzfunktion wirst du die Stellen eins und vier berechnen. Die Methode zwei ist also äquivalent mit der Methode eins und du erhältst natürlich dasselbe Ergebnis. Es gilt somit: 14f(x)dx-14g(x)dx=14(fx-g(x))dx=9. Jetzt müssen wir noch eine letzte Frage klären. Was passiert, wenn wir g und f nach unten oder oben verschieben? Ersetzen wir f(x) einfach durch f(x)+c und g(x) durch g(x)+c, wobei c irgendeine reelle Zahl ist. Wenn wir jetzt aber das Integral fx+c-(g(x)+c)dx bilden, dann hebt sich die Verschiebung c wieder heraus und wir erhalten fx-g(x)dx. Anders kann es ja gar nicht sein. Schließlich bleibt beim gemeinsamen Verschieben die Lage der beiden Graphen zueinander gleich. Wir fassen zusammen: 1. Der Flächeninhalt A der Fläche, die durch die Graphen der beiden Funktionen f und g begrenzt wird, ist gegeben durch A=abf(x)-g(x)dx. Dabei sind a und b die x-Werte der Schnittpunkte. Und f steht für die Funktion, die im Intervall [a;b] oberhalb verläuft. g steht dementsprechend für die Funktion, die im Intervall [a;b] unterhalb verläuft. 2. Es gilt: A=abf(x)dx-abg(x)dx=ab(fx-g(x))dx. Tschüss.
Fläche zwischen Funktionsgraphen mit Integralen berechnen Übung
-
Beschreibe die Problemstellung zur Berechnung der Fläche zwischen zwei Funktionsgraphen.
TippsMithilfe des Integrals berechnen wir Flächen zwischen einem Funktionsgraphen und der x-Achse in einem bestimmten Intervall.
Fertige eine Skizze des Problems an und vollziehe die Vorgehensweise nach.
Die Fläche zwischen zwei Funktionsgraphen verändert sich nicht, wenn man beide Funktionsgraphen gleichartig verschiebt.
LösungWir haben zuvor gelernt, dass man mithilfe des Integrals einer Funktion die Fläche unterhalb dieser (bis zur x-Achse) berechnen kann. Nun möchten wir durch das Zurückführen auf das bereits Erlernte die Fläche zwischen zwei Funktionen berechnen.
Im einfachsten Fall schneiden sich zwei Funktionen an zwei Schnittpunkten und erzeugen somit eine Fläche oberhalb der x-Achse, welche wir berechnen wollen. Verschieben wir diese Funktionen gleichermaßen nach unten, sodass sie unterhalb der x-Achse sind, so ändert sich der Flächeninhalt zwischen den beiden Graphen nicht.
Sollten die Funktionen sich an mehr als zwei Punkten schneiden, so berechnen wir den gesamten Flächeninhalt, indem wir von Schnittpunkt zu Schnittpunkt jeweils die Teilflächen berechnen und addieren.
-
Beschreibe die Methoden zur Berechnung der Fläche zwischen zwei Funktionsgraphen.
TippsSkizziere das Vorgehen beider Methoden.
Entsprechen die Integrationsgrenzen $a$ und $b$ den $x$- oder den $y$-Koordinaten der Schnittpunkte von $f$ und $g$?
Wie nennt man die Schnittpunkte der Funktion $h$ mit der $x$-Achse?
LösungMan unterscheidet zwei Methoden zur Berechnung der Fläche zwischen zwei Funktionsgraphen, welche jedoch rechnerisch auf das Gleiche hinauslaufen:
- Wir können als Erstes die Schnittpunkte der Graphen von $f$ und $g$ bestimmen, um deren $x$-Koordinaten als Integrationsgrenzen zu verwenden. Anschließend berechnen wir jeweils die Fläche unter $f$ und $g$. Der Betrag der Differenz der Flächeninhalte ergibt unsere gesuchte Fläche.
- Mithilfe einer Differenzenfunktion $h$, welche wir durch die Differenz von $f(x)$ und $g(x)$ erhalten, können wir die gesuchte Fläche ebenfalls berechnen. Die Nullstellen der Differenzenfunktion entsprechen den $x$-Koordinaten der Schnittpunkte von $f$ und $g$ und dienen ebenfalls als Integrationsgrenzen. Die Fläche zwischen dem Graphen von $h$ und der $x$-Achse entspricht dann der gesuchten Fläche zwischen $f$ und $g$.
-
Berechne den Flächeninhalt der von $f$ und $g$ eingeschlossenen Fläche.
TippsDie Integrationsgrenzen entsprechen den x-Koordinaten der Schnittpunkte der Funktionen.
Der Hauptsatz der Differential- und Integralrechnung besagt:
$\int\limits_{a}^{b} f(x) dx= \left[ F(x) \right]_a^b= F(b)- F(a)$
Achte darauf, welche Funktion oberhalb der anderen liegt oder verwende alternativ Betragsstriche, denn negative Flächeninhalte gibt es nicht.
LösungWir berechnen als Erstes die Schnittpunkte der Funktionen $f(x)=x^2+x+2$ und $g(x)=-x^2+5x+8$. Dazu setzen wir Funktionen gleich, formen um und wenden die p-q-Formel an:
$\begin{align*} f(x) &= g(x) \\ x^2+x+2 &= -x^2+5x+8 &|& +x^2-5x-8 \\ 2x^2 -4x - 6 &= 0 &|& :2 \\ x^2 -2x -3 &= 0 \\ x_{1,2} &=1 \pm \sqrt{1+3} \end{align*}$
Das ergibt $x_1 =3$ und $x_2 = -1$. Somit haben wir die Integrationsgrenzen $a=-1$ und $b=3$ festgelegt.
Da der Graph von $g$ oberhalb des Graphen von $f$ liegt, berechnen wir die Differenz $A= A_g - A_f$ und wenden den Hauptsatz der Differential- und Integralrechnung an:
$\begin{align*} A &= \int\limits_{-1}^{3} (g(x)-f(x)) dx \\ &= \int\limits_{-1}^{3} (-2x^2+4x+6)dx \\ &= \left[ -\frac{2}{3} x^3+2x^2+ 6x \right]_{-1}^3 =F(3)-F(-1)=\frac{64}{3}~\text{FE} \approx 21,33~\text{FE} \end{align*}$
-
Ermittle den gesamten Flächeninhalt $A$ der von $f$ und $g$ eingeschlossenen Fläche.
TippsUm die $x$-Koordinaten der Schnittpunkte zu ermitteln, kannst du die Funktionsgleichungen gleichsetzen und anschließend nach $x$ umformen.
Wende den Satz: „Ein Produkt ist gleich Null, wenn mindestens ein Faktor gleich Null ist“ an, um die Integrationsgrenzen zu ermitteln.
Wähle als Integrationsgrenzen stets zwei nebeneinanderliegende Schnittstellen aus. Wie viele Teilflächen musst du dann berechnen?
Der Hauptsatz der Differential- und Integralrechnung besagt:
$\int\limits_{a}^{b} f(x) dx= \left[ F(x) \right]_a^b= F(b)- F(a)$
Fertige eine Skizze für diesen Sachverhalt an.
LösungAls Erstes berechnen wir die Schnittstellen der gegebenen Funktionen $f$ und $g$, indem wir die Funktionsgleichungen gleichsetzen und nach $x$ auflösen:
$\begin{align*} f(x) &= g(x) \\ x^3-4x &= 5x \\ x^3-9x &= 0 \\ x \cdot (x^2-9) &= 0 \\ x \cdot (x+3) \cdot (x-3) &= 0 \end{align*}$
Damit sind also $x_1=0$, $x_2=-3$ und $x_3=3$ die möglichen Lösungen. Gesucht sind daher die Flächen, die von den Graphen in dem abgeschlossenen Intervall $I_1=[-3;0]$ und $I_2=[0;3]$ eingeschlossen werden.
Im ersten Intervall liegt der Graph von $f$ oberhalb des Graphen von $g$, im zweiten Intervall umgekehrt. Durch eine Skizze oder durch eine Probeeinsetzung eines Wertes innerhalb der Intervalle kannst du dies herausfinden.
$\begin{align*} A_1 &= \int\limits_{-3}^{0} (f(x)-g(x)) dx= \int\limits_{-3}^{0} (x^3 -9x)dx = \left[ \frac{1}{4}x^4 - \frac{9}{2} x^2 \right]_{-3}^0 \\ &=F(0)-F(-3)=\frac{81}{4}~\text{FE} = 20,25~\text{FE} \\ A_2&= \int\limits_{0}^{3} (g(x)-f(x)) dx= \int\limits_{0}^{3} ( -x^3 + 9x)dx = \left[ -\frac{1}{4}x^4 + \frac{9}{2} x^2 \right]_{0}^3 \\ &=F(3)-F(0)=\frac{81}{4}~\text{FE} = 20,25~\text{FE} \end{align*}$
Nun addieren wir die Flächeninhalte der Teilflächen, um den gesamten Flächeninhalt der eingeschlossenen Flächen zu erhalten:
$A= A_1 + A_2 = 20,25~\text{FE} + 20,25~\text{FE} = 40,5~\text{FE}$.
-
Berechne den Flächeninhalt zwischen den Funktionsgraphen $f(x)$ und $g(x)$.
TippsWie bestimmt man die Integrationsgrenzen?
Der Hauptsatz der Differential- und Integralrechnung besagt: $\int\limits_{a}^{b} f(x) dx= \left[ F(x) \right]_a^b= F(b)- F(a)$
LösungZwei Funktionen $f(x)=-x^2+6x-3$ und $g(x)=x^2-4x+5$ sind gegeben und die Fläche zwischen den beiden Funktionen ist gesucht. Wir beginnen mit der Bestimmung der Integrationsgrenzen, indem wir die x-Koordinaten der Schnittpunkte der Funktionen bestimmen. Wir setzen die Funktionen gleich und erhalten durch Äquivalenzumformungen und der Anwendung der p-q-Formel die Integrationsgrenzen:
$\begin{align*} f(x) &= g(x) \\ -x^2+6x-3 &= x^2-4x+5 &|& -x^2+4x-5 \\ -2x^2+10x-8 &= 0 &|& :(-2) \\ x^2-5x+4 &= 0 \\ x_{1,2} &=2,5 \pm \sqrt{2,5^2-4} \end{align*} $
Wir erhalten also $x_1 = 1$ und $x_2 = 4$. Da der Graph von $f$ oberhalb des Graphen von $g$ liegt, berechnen wir die Differenz und wenden den Hauptsatz der Differential- und Integralrechnung an:
$\begin{align*} A&=A_f - A_g\\ &=\int\limits_{1}^{4} f(x) dx - \int_{1}^{4} g(x) dx \\ &= \int\limits_{1}^{4} (f(x)-g(x)) dx\\ &= \int\limits_{1}^{4} (-2x^2+10x-8)dx\\ &= \left[ -\frac{2}{3} x^3+5x^2-8x \right]_1^4 =F(4)-F(1) =9~FE\end{align*} $.
-
Bestimme den Parameter $a$.
TippsBerechne als Erstes die Schnittstellen, also die Integrationsgrenzen.
Wende den Satz „Ein Produkt ist gleich Null, wenn mindestens ein Faktor gleich Null ist“ an, um die Integrationsgrenzen zu ermitteln.
Bedenke beim Integrieren, dass $a$ ein Parameter und nicht die Integrationsvariable ist.
Setze den Term, den du mithilfe des Hauptsatzes der Differential- und Integralrechnung erhältst, gleich dem gegebenen Flächeninhalt und löse die Gleichung nach $a$ auf.
LösungWir beginnen mit der Berechnung der Integrationsgrenzen, indem wir die Funktionsgleichungen $f(x)=x^2$ und $g(x)=ax$ gleichsetzen und nach $x$ auflösen:
$\begin{align*} f(x) &= g(x) \\ x^2 &= ax \\ x^2-ax &= 0 \\ x \cdot (x-a) &= 0 \end{align*}$
Die Lösungen lauten also $x_1=0$ und $x_2=a$. Wir wissen, dass die Fläche, die von den Graphen in dem abgeschlossenen Intervall $I=[0;a]$ eingeschlossen wird, $A=4,5~\text{FE}$ beträgt.
$\begin{align*} A&= \int\limits_{0}^{a} (g(x)-f(x)) dx= \int\limits_{0}^{a} (ax-x^2)dx \\ &= \left[ \frac{a}{2}x^2 - \frac{1}{3} x^3 \right]_{0}^a=F(a)-F(0)= \frac{1}{2}a^3 - \frac{1}{3} a^3 = \frac{1}{6} a^3 \end{align*}$
Da wir wissen, dass $A=4,5~\text{FE}$, setzen wir $ \frac{1}{6} a^3 = 4,5$ und lösen nach $a$ auf:
$\begin{align*} \frac{1}{6} a^3 &= 4,5 &|& \cdot 6 \\ a^3 &= 27 &|& \sqrt[3]{~~}\\ a &= 3 \end{align*}$
Der gesuchte Wert für den Parameter $a$ lautet also $a=3$.
9.897
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.311
Lernvideos
38.669
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?











Hallo Itslearning Nutzer 2535 62376,
kannst du genauer sagen, welche Stelle du meinst?
Liebe Grüße aus der Redaktion
Das Ergebnis ist falsch, es müssen -21,33 FE sein.
@Annemarie K.:
Bei der Intergral-Schreibweise reicht es zwischen dem Integral-Zeichen und dx die Funktion f(x) - g(x) ohne Klammern zu schreiben, da klar sein sollte, dass man f(x) - g(x) zusammen integriert.
Erst am Ende kommt das dx, welches den zu integrierenden Teil abschließt.
Wir hoffen, das war hilfreich :)
Integral [f(x) -g(x)]dx
warum lassen Sie die Klammern weg?
Integral(-2x² +10x -8)dx
@Nj1:
Wenn du eine Skizze der Funktionsgraphen hast, kannst du daran ablesen, welcher der beiden Funktionsgraphen in dem betrachteten Bereich oberhalb vom anderen liegt, z. B. f(x). Dann ziehst du im Integral die "untere" Funktion von der "oberen" ab, im Beispiel wäre das f(x)-g(x).
Allerdings ändert sich der Wert des Integral nicht, wenn du es umgekehrt machst. Ich erkläre es dir kurz, falls es dich interessiert. Du kannst um f(x)-g(x) geschickt eine Minusklammer erzeugen:
f(x)-g(x) = -( -f(x)+g(x) ) = -( g(x)-f(x) )
und mit den Beträgen |.| innerhalb der Integralrechnung erhältst du:
| f(x)-g(x) | = | -( g(x)-f(x) ) | = | g(x)-f(x) |
Ich hoffe, ich konnte dir weiterhelfen. Melde dich bei weiteren Fragen gerne wieder. Gerne kannst du dich auch an den Fach-Chat oder an die Lehrerbox wenden.
Liebe Grüße aus der Redaktion