Skalarprodukt
Das Skalarprodukt benötigst du in der analytischen Geometrie sehr häufig. Du kannst es verwenden, um den von zwei Vektoren aufgespannten Winkel oder die Fläche des dazugehörigen Parallelogramms zu berechnen. Weiter kannst du mit dem Skalarprodukt einfach Orthogonalität oder Kollinearität nachweisen.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Vektor?
- Was ist ein Skalarprodukt?
- Multiplikation eines Vektors mit einer Zahl
- Das Skalarprodukt
- Eine praktische Berechnung des Skalarproduktes
- Rechenregeln
- Beispiele für das Skalarprodukt
Was ist ein Vektor?
Ein Vektor, zum Beispiel $\vec a$, hat im $\mathbb{R}^2$ zwei und im $\mathbb{R}^3$ drei Koordinaten. Diese Koordinaten werden entweder mit den Indizes $1$, $2$ (, $3$) oder auch mit $x$, $y$ (, $z$) bezeichnet und spaltenweise aufgeschrieben. Der Vektor $\vec a$ sieht im $\mathbb{R}^2$ so
$\vec a=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}=\begin{pmatrix} a_x \\ a_y \end{pmatrix}$
und im $\mathbb{R}^3$ so
$\vec a=\begin{pmatrix} a_1 \\ a_2\\ a_3 \end{pmatrix}=\begin{pmatrix} a_x \\ a_y\\ a_z \end{pmatrix}$
aus. Sowohl der $\mathbb{R}^2$ als auch der $\mathbb{R}^3$ sind euklidische Vektorräume. In diesen ist das Skalarprodukt definiert.
Was ist ein Skalarprodukt?
Multiplikation eines Vektors mit einer Zahl
Wenn du einen Vektor mit einer Zahl multipliziert, nennt man diese eine skalare Multiplikation oder ein skalares Produkt. Du multiplizierst jede Koordinate des Vektors mit einem Skalar, also einer reellen Zahl. Das Ergebnis ist ein Vektor.
$3\cdot \begin{pmatrix} 1 \\ 3\\ -2 \end{pmatrix}=\begin{pmatrix} 3\cdot 1 \\ 3\cdot 3\\ 3\cdot (-2) \end{pmatrix}=\begin{pmatrix} 3 \\ 9\\ -6 \end{pmatrix}$
Unterscheide diese Multiplikation unbedingt von dem Skalarprodukt.
Das Skalarprodukt
Seien zwei Vektoren $\vec a$ sowie $\vec b$ gegeben, dann ist das Skalarprodukt oder auch das innere Produkt dieser beiden Vektoren wie folgt definiert:
$ \vec a\cdot \vec b=\cos(\alpha)\cdot |\vec a|\cdot |\vec b|$.
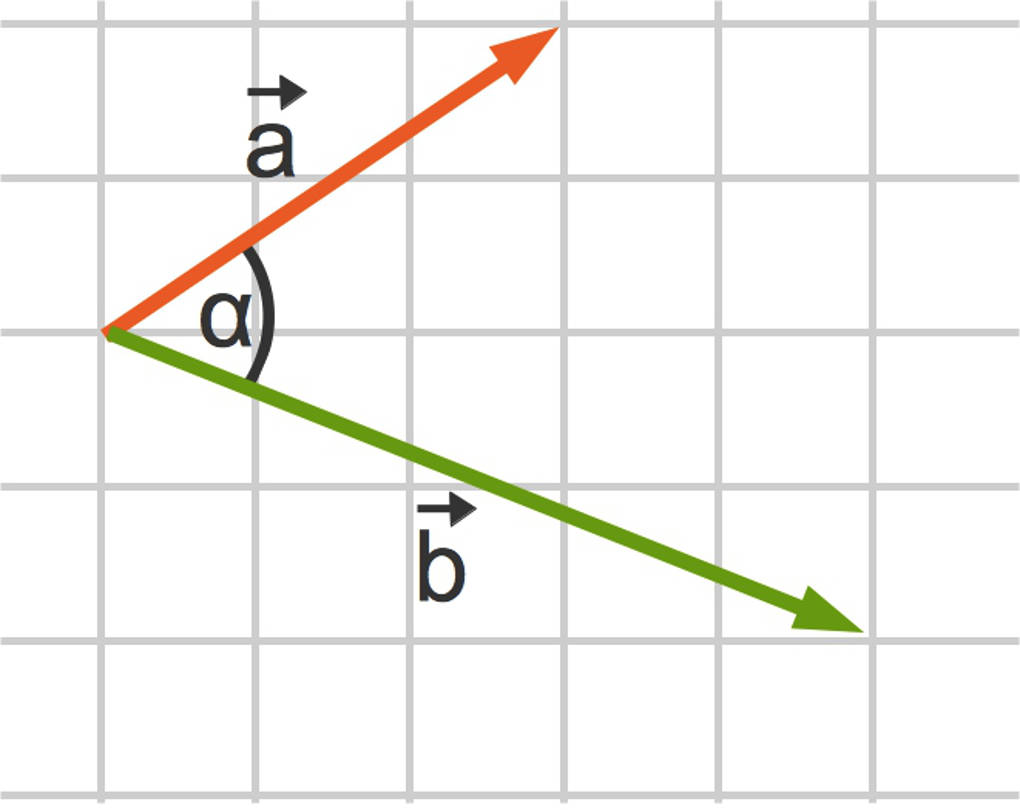
Dabei ist $\alpha$ der von den beiden Vektoren eingeschlossene Winkel und $|\vec a|$ sowie $|\vec b|$ der Betrag oder auch die Länge der Vektoren $\vec a$ beziehungsweise $\vec b$. Da sowohl der Cosinus eines Winkels als auch die Längen von Vektoren Zahlen sind, also Skalare, ist auch deren Produkt eine Zahl. Das bedeutet: Das Ergebnis eines Skalarproduktes ist eine Zahl. Daher kommt auch der Name.
Eine praktische Berechnung des Skalarproduktes
Das Skalarprodukt kann auch folgendermaßen berechnet werden.
- Du multiplizierst die einander entsprechenden Koordinaten der beiden Vektoren und
- addierst diese Produkte.
Das bedeutet also
$\vec a\cdot \vec b=a_x\cdot b_x+a_y\cdot b_y$
im $\mathbb{R}^2$ sowie
$\vec a\cdot \vec b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z$
im $\mathbb{R}^3$.
Beachte:
- Üblicherweise wird auch beim Skalarprodukt das Malzeichen $\cdot$ verwendet. Im entsprechenden Kontext ist es jedoch eindeutig, dass damit das Skalarprodukt zweier Vektoren gemeint ist.
- Es gibt auch ein Vektorprodukt. Auch bei diesem werden zwei Vektoren multipliziert. Das Ergebnis ist dann allerdings ein Vektor. Diese Produkt wird auch als Kreuzprodukt bezeichnet. Um die beiden Produkte zu unterscheiden, wird das "$\times$"-Zeichen verwendet: $\vec a \times \vec b$.
Rechenregeln
- Das Skalarprodukt ist kommutativ: $\vec a\cdot \vec b=\vec b\cdot \vec a$.
- Es gelten die folgenden Distibutivgesetze für die skalare Multiplikation:
$\qquad (r+s)\cdot \vec a=r\cdot \vec a+s\cdot \vec a$ sowie
$\qquad r\cdot(\vec a+\vec b)=r\cdot \vec a+r\cdot\vec b$.
Beispiele für das Skalarprodukt
- $\begin{pmatrix} 1 \\ 3 \end{pmatrix}\cdot\begin{pmatrix} -2 \\ 2 \end{pmatrix}=1\cdot (-2)+3\cdot 2=-2+6=4$
- $\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix}\cdot\begin{pmatrix} 1 \\ -1 \\ 2\end{pmatrix}=3\cdot 1+4\cdot (-1)+5\cdot 2=3-4+10=9$
Anwendungen des Skalarproduktes
Das Skalarprodukt benötigst du in der analytischen Geometrie sehr häufig. Hier siehst du die wesentlichen Anwendungen und / oder Sonderfälle des Skalarproduktes.
Berechnung des von zwei Vektoren eingeschlossenen Winkels
Durch Umformung der Formel
$ \vec a\cdot \vec b=\cos(\alpha)\cdot |\vec a|\cdot |\vec b|$
erhältst du
$\cos(\alpha)=\frac{\vec a\cdot \vec b}{|\vec a|\cdot |\vec b|}$.
Damit kannst du den von den beiden Vektoren $\vec a$ und $\vec b$ eingeschlossenen Winkel berechnen.
Wir schauen uns hierfür ein Beispiel an:
$\vec a=\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix}; ~~\vec b=\begin{pmatrix} 1 \\ -1 \\ 2\end{pmatrix}$
Dann ist:
$\cos(\alpha)=\frac{9}{\sqrt{50}\cdot \sqrt6}$.
Dabei ist die Länge eines Vektors $|\vec a|=\sqrt{a_x^2+a_y^2+a_z^2}$. Durch Umkehrung des Cosinus erhältst du den gesuchten Winkel:
$\alpha=\cos^{-1}\left(\frac{9}{\sqrt{50}\cdot \sqrt6}\right)\approx 58,7^\circ$.
Kollinearität von Vektoren
Es gilt die sogenannte Cauchy-Schwarz'sche-Ungleichung $\vec a\cdot \vec b\le|\vec a|\cdot |\vec b|.$ Wenn du dir noch einmal die Formel für das Skalarprodukt anschaust
$ \vec a\cdot \vec b=\cos(\alpha)\cdot |\vec a|\cdot |\vec b|$
erkennst du, dass in der Ungleichung nur dann die Gleichheit gilt, wenn $\cos(\alpha)=1$ ist, also $\alpha=0^\circ$. Das bedeutet, dass die Vektoren kollinear sind. Sie schließen also einen $0^\circ$-Winkel oder damit gleichbedeutend einen $180^\circ$-Winkel ein.
Orthogonalität von Vektoren
Ein weiterer Sonderfall liegt vor, wenn $\vec a\cdot \vec b=0$ ist. Dann ist $\cos(\alpha)=0$, damit ist $\alpha=90^\circ$.
Merke dir: Wenn zwei Vektoren orthogonal zueinander sind, das heißt, den Winkel $90^\circ$ einschließen, dann ist deren Skalarprodukt $0$. Diese Aussage gilt auch umgekehrt.
$\vec a\perp\vec b~\Leftrightarrow~\vec a\cdot \vec b=0$
Zum Beispiel sind die Vektoren
$\vec a=\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix};~~\vec b=\begin{pmatrix} 4 \\ 2 \\ -4\end{pmatrix}$
orthogonal zueinander, da gilt:
$\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix}\cdot\begin{pmatrix} 4 \\ 2 \\ -4\end{pmatrix}=3\cdot 4+4\cdot 2+5\cdot (-4)=12+8-20=0$
Flächenberechnung: Parallelogramm
Der Flächeninhalt eines Parallelogramms, welches von zwei Vektoren aufgespannt wird, kann mit Hilfe des Skalarproduktes berechnet werden.
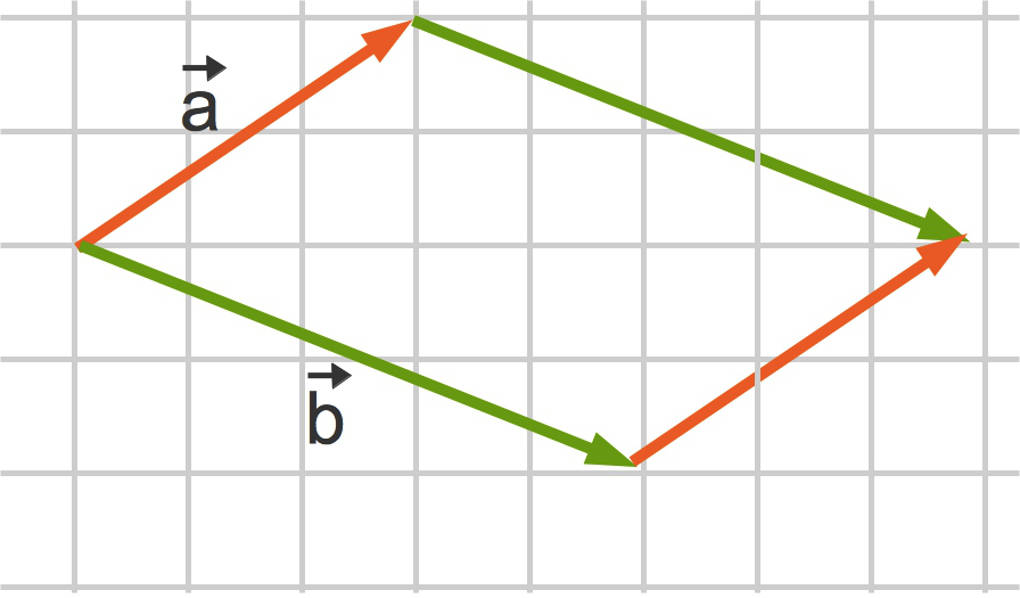
Für den Flächeninhalt eines Parallelogrammes gilt:
$A_{\text{Parallelogramm}}=\sqrt{|\vec a|^2\cdot |\vec b|^2-\left(\vec a\cdot \vec b\right)^2}$.
Flächenberechnung: Dreieck
Um den Flächeninhalt eines Dreiecks zu berechnen, verwendest du die gleiche Formel wie bei einem Parallelogramm, nur musst du noch durch $2$ dividieren.
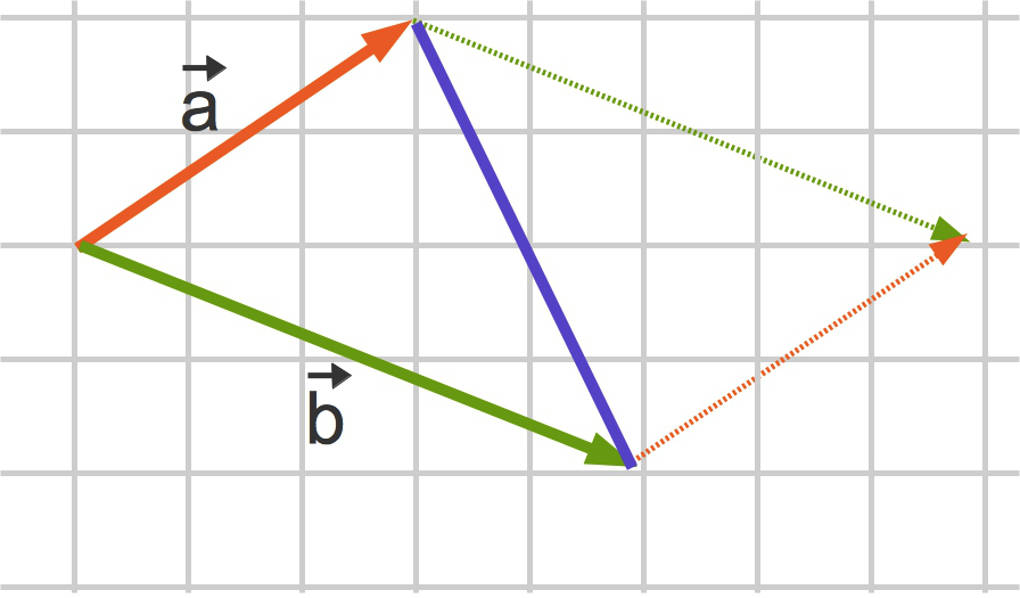
Für den Flächeninhalt eines Dreiecks gilt dementsprechend:
$A_{\text{Dreieck}}=\frac12\cdot\sqrt{|\vec a|^2\cdot |\vec b|^2-\left(\vec a\cdot \vec b\right)^2}$.
Beispiel
Betrachte das Dreieck $\Delta_{PQR}$:
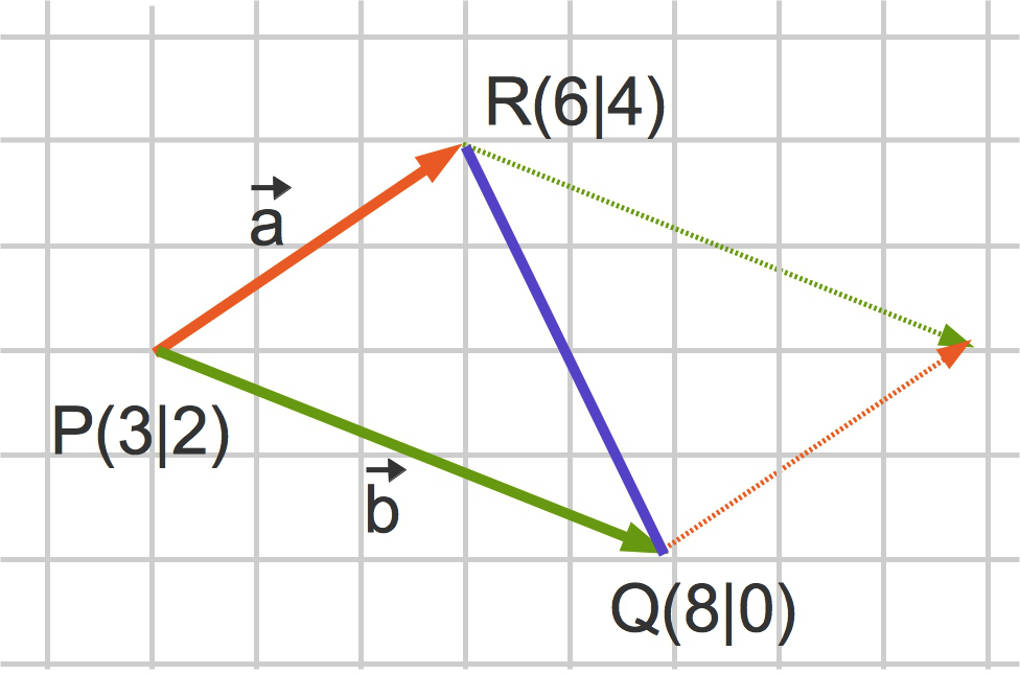
- $\vec a=\vec{PR}=\begin{pmatrix} 3 \\ 2 \end{pmatrix}$
- $|\vec a|=\sqrt{3^2+2^2}=\sqrt{13}$
- $\vec b=\vec{PQ}=\begin{pmatrix} 5 \\ -2 \end{pmatrix}$
- $|\vec b|=\sqrt{5^2+(-2)^2}=\sqrt{29}$
- $\vec a\cdot \vec b=15-4=11$
Nun kann die obige Formel angewendet werden:
$A_{\Delta_{PQR}}=\frac12\cdot\sqrt{13\cdot 29-11^2}=\frac12\cdot \sqrt{256}=\frac12\cdot16=8$ [FE] .
Alle Videos zum Thema
Videos zum Thema
Skalarprodukt (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Skalarprodukt (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung








 Skalarprodukt – Winkel zwischen zwei Vektoren
Skalarprodukt – Winkel zwischen zwei Vektoren
 Skalarprodukt – Flächeninhalte von Parallelogrammen und Dreiecken
Skalarprodukt – Flächeninhalte von Parallelogrammen und Dreiecken
 Skalarprodukt – Elementargeometrische Beweise
Skalarprodukt – Elementargeometrische Beweise
 Skalarprodukt
Skalarprodukt









