Rechnen mit Vektoren
In der analytischen Geometrie lernst du Vektoren kennen. Du kannst mit Vektoren auch rechnen – sogar so ähnlich wie du es von den reellen Zahlen kennst.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Überblick
Vektoren beschreiben Bewegungen oder Verschiebungen in der Ebene ($\mathbb{R}^{2}$) oder im Raum ($\mathbb{R}^{3}$). Du sprichst dann entsprechend von zweidimensionalen oder dreidimensionalen Vektoren.
Im Folgenden lernst du verschiedene Rechenoperationen für Vektoren kennen. Dabei kannst du immer wieder auf die entsprechenden Operationen im Eindimensionalen, also der Menge der reellen Zahlen $\mathbb{R}$, zurückgreifen.
Am Ende erhältst du noch einen Ausblick über weitere Rechenoperationen für Vektoren.
Vektoraddition und Vektorsubtraktion
Du kannst Vektoren addieren oder auch subtrahieren. Hierfür müssen sie allerdings aus dem gleichen Vektorraum kommen. Was bedeutet das konkret? Du kannst zum Beispiel einen zweidimensionalen Vektor nicht zu einem dreidimensionalen addieren. Umgekehrt heißt das, dass die Vektoren entweder alle zwei- oder dreidimensional sein müssen.
Die Addition von Vektoren
Du addierst zwei Vektoren, indem du die einzelnen Koordinaten der Vektoren addierst. So erhältst du wieder einen Vektor, den Summenvektor.
Schau dir ein Beispiel an:
$\begin{pmatrix} 1\\ -1\\3 \end{pmatrix}+ \begin{pmatrix} 4 \\ 1\\-2 \end{pmatrix}=\begin{pmatrix} 1+4\\ -1+1\\3-2 \end{pmatrix}=\begin{pmatrix} 5\\ 0\\1 \end{pmatrix}$
Die anschauliche Bedeutung der Vektoraddition kannst du hier im Bild sehen:
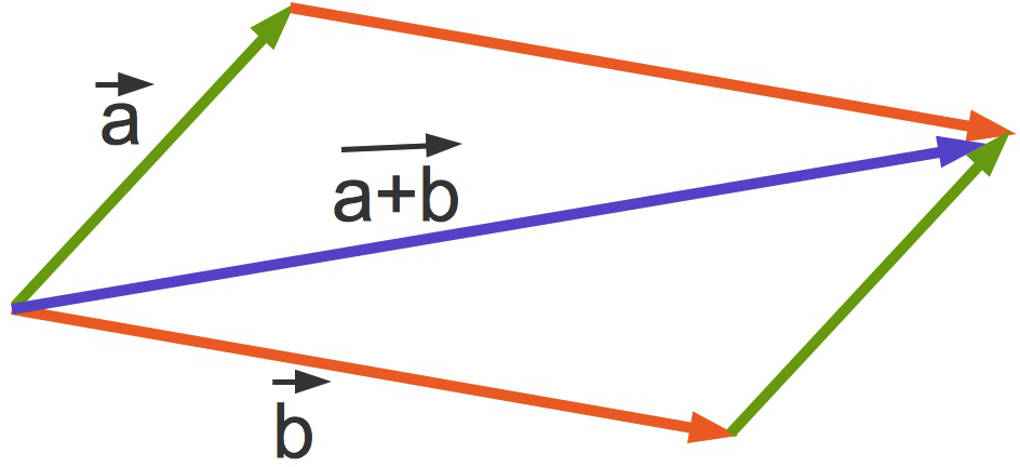
Die Subtraktion von Vektoren
Bei der Subtraktion gehst du ähnlich vor: Du subtrahierst die Vektoren koordinatenweise. Du erhältst als Ergebnis den Differenzvektor.
Am besten verstehst du dies anhand eines Beispiels:
$\begin{pmatrix} 2\\ 1\\5 \end{pmatrix}- \begin{pmatrix} 4 \\ 4\\-6 \end{pmatrix}=\begin{pmatrix} 2-4\\ 1-4\\5-({-6}) \end{pmatrix}=\begin{pmatrix} -2\\ -3\\11 \end{pmatrix}$
Die Vektorsubtraktion kannst du dir auch so vorstellen: $\vec a-\vec b=\vec a+\left(-\vec b\right)$. Du addierst also zu $\vec a$ den Gegenvektor $-\vec b$ von $\vec b$. Der Gegenvektor zeigt genau in die entgegengesetzte Richtung des Vektors.
Skalare Multiplikation
Du kannst einen Vektor auch mit einer Zahl multiplizieren. In der analytischen Geometrie werden Zahlen auch als Skalare bezeichnet. Daher kommt auch der Name skalare Multiplikation. Hierfür multiplizierst du jede Koordinate eines Vektors mit dem Skalar. Du erhältst dann ein Vielfaches eines Vektors.
Hierfür schauen wir uns ein Beispiel an:
$5\cdot\begin{pmatrix} 3\\ 1\\-2 \end{pmatrix}=\begin{pmatrix} 5\cdot 3 \\ 5\cdot 1\\5\cdot({-2}) \end{pmatrix}=\begin{pmatrix} 15\\ 5\\-10 \end{pmatrix}$
Übrigens, wenn ein Vektor sich als Vielfaches eines anderen Vektors darstellen lässt, sind die beiden Vektoren kollinear.
Schließlich kannst du alle nun gelernten Operationen auch gemeinsam durchführen. Im folgenden Bild sei $\vec a$ der blaue, $\vec b$ der gelbe und $\vec c$ der violette Pfeil. Dann erhältst du durch $2\cdot \vec a+6\cdot \vec b+3\cdot \vec c$ eine Linearkombination oder auch Vektorzug aus den Vektoren $\vec a$, $\vec b$ und $\vec c$.
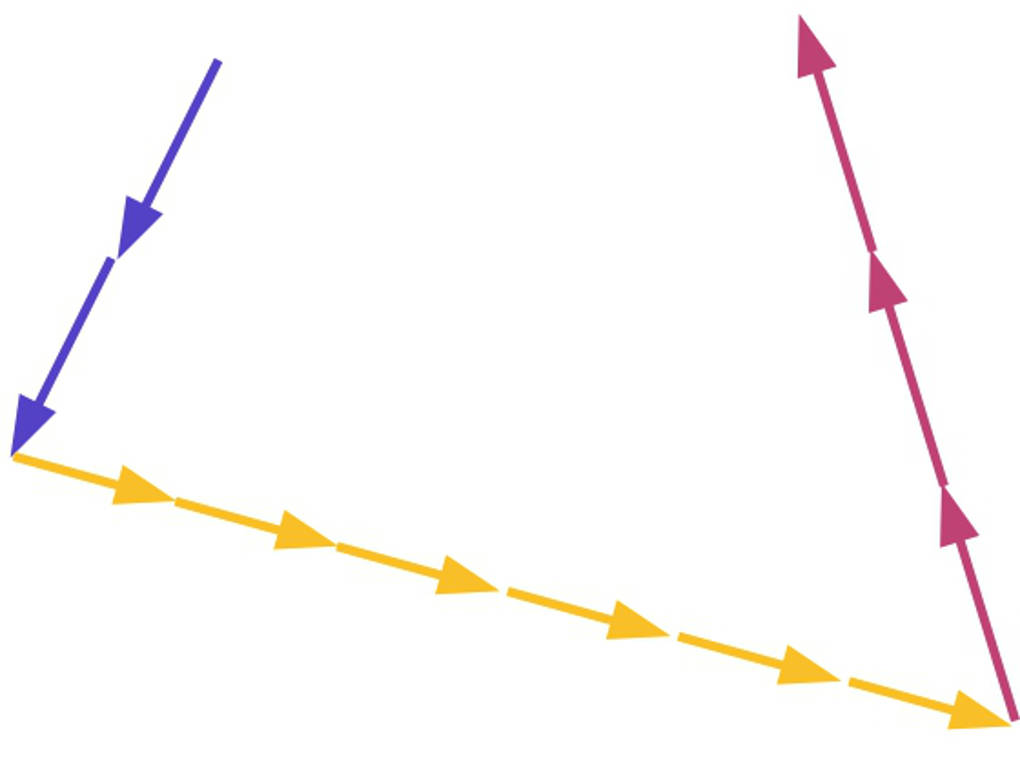
Rechengesetze
Wir schauen uns nun noch die Rechengesetze in Bezug auf Vektoren an:
Das Kommutativgesetz
Das Kommutativgesetz kennst du vielleicht auch als Vertauschungsgesetz: Bei der Vektoraddition darfst du die Reihenfolge vertauschen: $\vec a+\vec b=\vec b+\vec a$.
Das Assoziativgesetz
Das Assoziativgesetz bei der Vektoraddition besagt, dass du entscheiden kannst, welche Vektoren du zuerst addierst. Manchmal kannst du damit eine Rechnung vereinfachen: $\left(\vec a+\vec b\right)+\vec c=\vec a+\left(\vec b+\vec c\right)$.
Das Distributivgesetz
Hier gelten zwei Distributivgesetze, je nachdem ob du Vektoren oder Skalare addierst:
- $r\cdot \left(\vec a+\vec b\right)=r\cdot \vec a+r\cdot \vec b$
- $(r+s)\cdot \vec a=r\cdot \vec a+s\cdot \vec a$
Das Distributivgesetz gilt übrigens auch, wenn du jeweils das Plus- durch ein Minuszeichen ersetzt.
Ausblick
Es gibt noch zwei weitere Rechenoperationen für Vektoren, welche allerdings hier nicht weiter behandelt werden:
- Das Skalarprodukt zweier Vektoren liefert als Ergebnis einen Skalar (eine Zahl). Daher kommt der Name.
- Das Kreuzprodukt oder auch Vektorprodukt zweier Vektoren liefert einen Vektor. Dieser Vektor steht senkrecht auf den beiden miteinander multiplizierten Vektoren.
Anwendungsaufgaben zur Vektorrechnung
Mithilfe der Vektorrechnung kann man in Sachzusammenhängen Längen und Winkel bestimmen. Die folgenden drei Beispiele setzten Kenntnisse des Vektorrechnens voraus und beziehen sich auf zwei- und dreidimensionale Räume.
Anwendungsbeispiel: Rechteck, Quadrat oder Raute?

Es soll überprüft werden, ob es sich um ein Rechteck (gelb), ein Quadrat (grün) oder eine Raute (rot) handelt, wenn die vier Eckpunkte durch folgende Koordinaten beschrieben sind:
$\begin{array}{llll} A (6|1|7); & B (5|1|8); & C (4|1|7); & D (5|1|6) \end{array}$
Um die Aufgabe zu lösen, sollten die Eigenschaften der Figuren berücksichtigt werden.
Das Rechteck hat jeweils zwei gleich lange gegenüberliegende Seiten und vier rechte Winkel, das Quadrat hat vier gleich lange Seiten und vier rechte Winkel und die Raute hat vier gleich lange Seiten.
Somit wird zunächst die Länge der Seiten, also die Vektorlänge wie folgt bestimmt:
$\vec{AB} = \left(\begin{array}{c} -1\\0\\1\\ \end{array}\right)$
$|\vec{AB}| = \sqrt{(-1)^2 + 0^2 + 1^ 2} = \sqrt{2}$
$\vec{BC} = \left(\begin{array}{c} -1\\0\\-1\\ \end{array}\right)$
$|\vec{BC}| = \sqrt{(-1)^2 + 0^2 + (-1)^ 2} = \sqrt{2}$
$\vec{CD} = \left(\begin{array}{c} 1\\0\\-1\\ \end{array}\right)$
$|\vec{CD}| = \sqrt{1^2 + 0^2 + (-1)^ 2} = \sqrt{2}$
$\vec{DA} = \left(\begin{array}{c} 1\\0\\1\\ \end{array}\right)$
$|\vec{DA}| = \sqrt{1^2 + 0^2 + 1^ 2} = \sqrt{2}$
Da der Betrag die Länge des Vektors angibt, fällt auf: Alle vier Seiten sind gleich lang, nämlich $\sqrt{2}$.
Somit kann bereits das Rechteck ausgeschlossen werden.
Um rechte Winkel nachzuweisen, prüft man, ob die Vektoren senkrecht (orthogonal) zueinander stehen. Dazu benutzt man das Skalarprodukt und berechnet, ob das Ergebnis Null ist:
$\vec{a}\cdot \vec{b} = a_1b_1 +a_2b_2 +a_3b_3 = 0$
Übertragen auf die Figur bedeutet dies:
$\vec{AB}\cdot \vec{BC} = (-1|0|1)^T\cdot (-1|0|-1)^T = 1 + 0 - 1 = 0$
$\vec{BC}\cdot \vec{CD} = (-1|0|-1)^T\cdot (1|0|-1)^T = -1 + 0 + 1 = 0$
$\vec{CD}\cdot \vec{DA} = (1|0|-1)^T\cdot (1|0|1)^T = 1 + 0 - 1 = 0$
Da die Skalarprodukte Null ergeben und die Seiten gleich lang sind, handelt es sich bei der Figur um ein Quadrat.
Anwendungsbeispiel: Winkel zwischen Vektoren
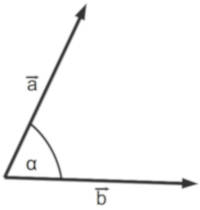
Wie groß ist der Winkel zwischen den Vektoren $a$ und $b$, welche wie folgt gegeben sind:
$\begin{array}{lll} \vec{a} = \begin{pmatrix}5 \\ 0 \end{pmatrix} && \vec{b} = \begin{pmatrix}1 \\ 3 \end{pmatrix} \end{array}$
Für den Winkel $\alpha$ zwischen den Vektoren $\vec{a}$ und $\vec{b}$ gilt:
$\cos(\alpha) = \frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}$
Setzt man die Vektoren aus der Aufgabenstellung ein, erhält man:
$\begin{array}{llll} \cos(\alpha) &=& \frac{\begin{pmatrix}5 \\ 0 \end{pmatrix}\cdot \begin{pmatrix}1 \\ 3 \end{pmatrix}}{\sqrt{5^{2} + 0^{2}}\cdot\sqrt{1^{2} + 3^{2}}}\\ &=& \frac{5 + 0}{5\cdot\sqrt{10}}\\ &=& \frac{5}{5\cdot\sqrt{10}}\\ &=& 0,316\\ \end {array}$
Um nun aus $\cos(\alpha)$ den Winkel $\alpha$ zu bestimmen, bildet man die Umkehrfunktion:
$\alpha = \cos^{-1}(0,316) \approx 71,57^\circ$
Anwendungsbeispiel: Rasenpyramide
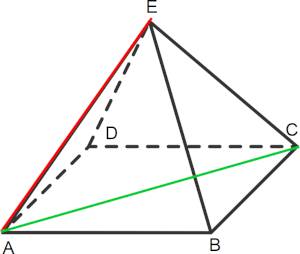
Die Rasenpyramide im Pyramidenpark Köln hat eine Höhe von $8\ \text{m}$ und eine quadratische Grundfläche mit Seitenlängen von $45\ \text{m}$.
- Wie groß ist der Neigungswinkel einer Kante zur Diagonalen am Boden?
- Wie viel Erde (in $\text{m}^{3}$) sind nötig, um die Pyramide aufzuschütten?
Die Berechnung des Neigungswinkels läuft darauf hinaus, mit der obigen Cosinus-Formel den Winkel $\alpha$ zu bestimmen:
$\cos(\alpha) = \frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}$
Zunächst legen wir die Pyramide so in ein dreidimensionales Koordinatensystem, dass sich folgende Eckpunkte ergeben:
- Für die quadratische Grundfläche: $A (45|0|0)$; $B (45|45|0)$; $C (0|45|0)$; $D (0|0|0)$
- Für die Pyramidenspitze: $E (22,5|22,5|8)$
Als Pyramidenkante wird $\vec{AE}$ gewählt und als $\vec{a}$ bezeichnet:
$\vec{a} =\vec{AE} = \left(\begin{array}{c} -22,5\\22,5\\8\\ \end{array}\right)$
$|\vec{a}| = \sqrt{(-22,5)^{2} + 22,5^{2} + 8^{2}}\approx32,81$
Die Diagonale am Boden ist dann $|AC|$, bezeichnet als Vektor $b$:
$\vec{b} = \vec{AC} = \left(\begin{array}{c} -45\\45\\0\\ \end{array}\right)$
$|\vec{b}| = \sqrt{(-45)^{2} + 45^{2} + 0^{2}}\approx63,64$
Eingesetzt in die Cosinus-Formel ergibt sich:
$\begin{array}{llll} \cos(\alpha) &=&\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}\\ &=& \frac{1012,5 + 1012,5 + 0}{32,81\cdot 63,64}\\ &=& \frac{2025}{2087,064}\\ &=& 0,97\\ \end {array}$
Damit folgt:
$\alpha = \cos^{-1}(0,97) \approx 14^\circ$
Der Neigungswinkel zwischen einer Pyramidenkante und einer Diagonalen am Boden beträgt also $14^\circ$.
Um herauszufinden, wie viel Erde zum Aufschütten der Pyramide nötig ist, wird die Volumenformel für Pyramiden verwendet. Die quadratische Grundfläche wird mit der Höhe multipliziert und durch $3$ geteilt:
$\begin{array}{llll} V &=& \frac{1}{3}\cdot G\cdot h\\ &=& \frac{1}{3}\cdot 45\ \text{m} \cdot 45\ \text{m}\cdot 8\ \text{m}\\ &=&5400\ \text{m}^{3}\\ \end {array}$
Zum Aufschütten der Rasenpyramide werden $5400\ \text{m}^{3}$ Erde benötigt.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Rechnen mit Vektoren (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Rechnen mit Vektoren (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Addition und Subtraktion von Vektoren
Addition und Subtraktion von Vektoren
 Skalare Multiplikation – Vielfache von Vektoren
Skalare Multiplikation – Vielfache von Vektoren









