Umfangswinkelsatz und Mittelpunktswinkelsatz
Umfangswinkel, Mittelpunktswinkel, Winkel am Kreis, Winkelbeziehung
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Umfangswinkel
Umfangswinkel (Peripheriewinkel) sind Winkel, die von zwei Sehnen eingeschlossen sind. Ihr Scheitelpunkt liegt auf einer Kreislinie (Peripherie des **Kreises.
Die Sehne hat hier, wie du dir schon denken konntest, nichts mit Muskeln zu tun. Sie beschreibt die Strecke zwischen zwei Punkten, die auf derselben Kreislinie liegen. Falls eine solche Sehne durch den Mittelpunkt $M$ eines Kreises geht, wird sie auch Durchmesser genannt.
Beim Scheitelpunkt treffen zwei Linien (hier Sehnen) aufeinander. In folgender Skizze sind zwei Umfangswinkel über der Sehne $\overline{AB}$ im Scheitelpunkt $C$ bzw. $C^*$ eingezeichnet:
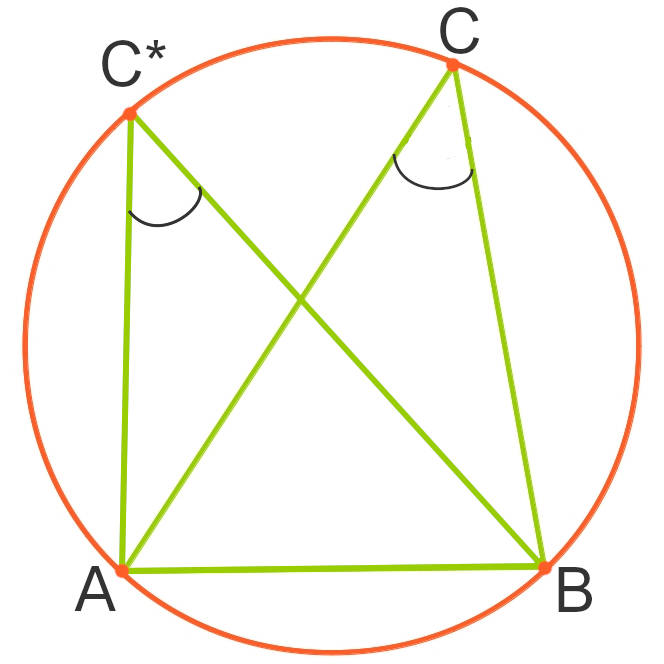
Es sieht so aus, als ob die Umfangswinkel gleich groß wären. Eine Skizze ist aber nicht perfekt. Es kann auch sein, dass deine Augen dich täuschen! Bevor wir die Antwort gemeinsam herausfinden, sieh dir noch einen anderen Winkel an, den Mittelpunktswinkel.
Mittelpunktswinkel
Mittelpunktswinkel (Zentriwinkel) sind Winkel, die von zwei gleichen Kreisradien eingeschlossen sind. Ihr Scheitel ist im Mittelpunkt $M$ des Kreises. Im Folgenden sind die beiden Winkel $\alpha$ und $\beta$ abgebildet.
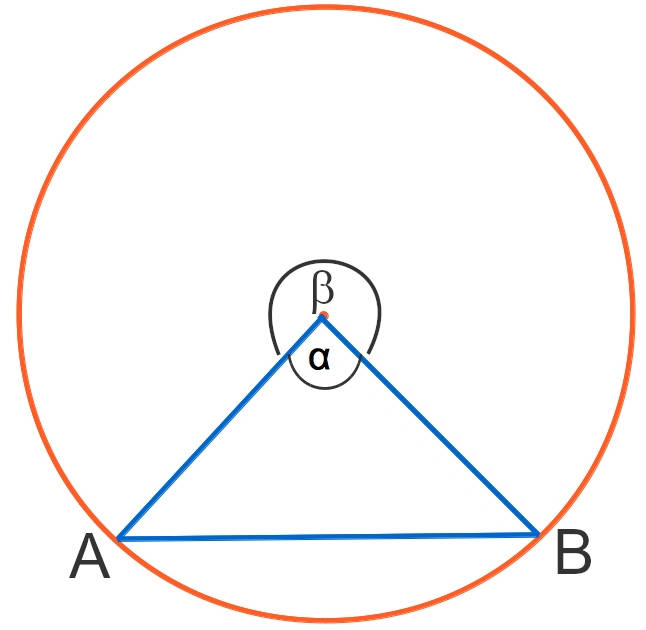
Aber nur einer der beiden ist der Mittelpunktswinkel zur Sehne $\overline{AB}$, nämlich $\alpha$. Als Mittelpunktswinkel ist tatsächlich immer der kleinere der beiden Winkel, die von zwei Kreisradien eingeschlossen werden, definiert.
Mittelpunktswinkelsatz
Gibt es einen Zusammenhang zwischen dem Umfangs- und dem Mittelpunktswinkel? Oder sind diese völlig unabhängig voneinander? Um diese Fragen beantworten zu können, zeichnest du einen beliebigen Umfangswinkel im Punkt $C$ zur Sehne $\overline{AB}$ ein. Jetzt zeichnest du von allen drei Punkten $A$, $B$ und $C$ jeweils den Radius zu $M$.
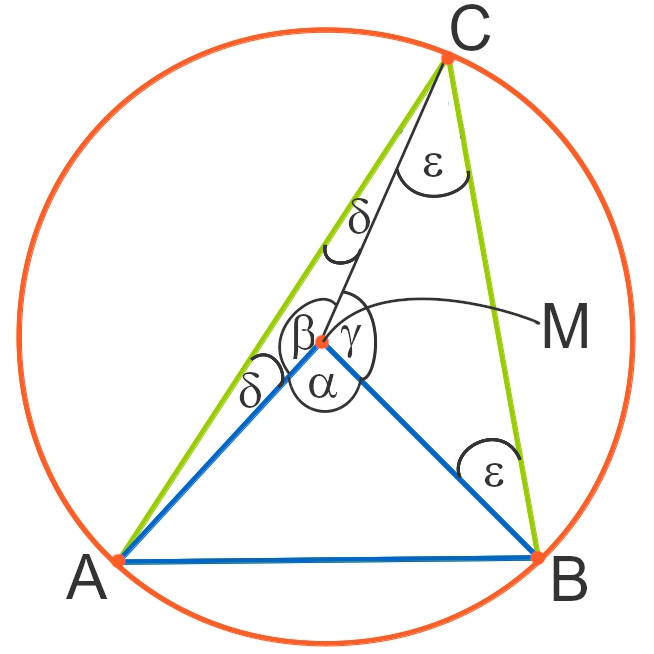
Es entstehen drei gleichschenklige Dreiecke, diese sind:
- $\Delta \text{AMC}$ mit den Basiswinkeln $\delta$
- $\Delta \text{MBC}$ mit den Basiswinkeln $\varepsilon$
- $\Delta \text{ABM}$ mit dem Mittelpunktswinkel $\alpha$
Der Umfangswinkel in dem Scheitelpunkt $C$ wurde aufgeteilt in die Winkel $\delta$ und $\varepsilon$. Deshalb ist er aber nicht verschwunden. Wenn du $\delta + \varepsilon$ rechnest, erhältst du den Umfangswinkel. Vielleicht erinnerst du dich, dass die drei Innenwinkel eines jeden Dreiecks gemeinsam immer $180^\circ$ ergeben. Es gilt also:
$\begin{array}{lrcll} \Delta \text{AMC}: & \delta + \delta + \beta & = & 180^\circ & \\ & 2\delta + \beta &=&180^\circ & |-2\delta\\ & \beta &=& 180^\circ-2 \delta & \\ \\ \Delta \text{MBC}: & \varepsilon + \varepsilon + \gamma & = & 180^\circ & \\ & 2\varepsilon + \gamma &=&180^\circ & |-2\varepsilon \\ & \gamma &=& 180^\circ-2 \varepsilon & \\ \end{array}$
Im Mittelpunkt $M$ treffen sich die Winkel $\alpha$, $\beta$ und $\gamma$. Gemeinsam ergeben sie einen Vollkreis und damit $360^\circ$. Für $\beta$ und $\gamma$ kannst du die Terme von oben einsetzen:
$\begin{array}{rcll} \alpha + \beta + \gamma & = & 360^\circ & \\ \alpha + (180^\circ-2\delta) + (180^\circ-2\varepsilon)& = & 360^\circ &\\ \alpha + 360^\circ - 2\delta - 2\varepsilon & = & 360^\circ & |-360^\circ\\ \alpha - 2\delta -2\varepsilon & = & 0 & |+2\delta + 2\varepsilon \\ \alpha & = & 2\delta + 2\varepsilon &\\ \alpha & = & 2(\delta + \varepsilon) & \\ \end{array}$
Du hast damit herausgefunden, dass der Mittelpunktswinkel $\alpha$ doppelt so groß ist wie der Umfangswinkel $\delta +\varepsilon$.
Umfangswinkelsatz
Auf diese Antwort folgt sofort die nächste Frage: Sind alle Umfangswinkel zu einer gegebenen Sehne $\overline{AB}$ immer gleich groß?
Überlege dir Folgendes: Das Dreieck $\Delta \text{ABM}$ ist fest. Damit ist auch der Mittelpunktswinkel $\alpha$ fest. Den Punkt $C$ können wir auf der Kreislinie oberhalb der Strecke $\overline{AB}$ frei wählen. Die Schenkel des Winkels in $C$ verändern sich also.
Doch der Winkel bleibt immer gleich groß, nämlich halb so groß wie der Mittelpunktswinkel $\alpha$!
Mit der Berechnung vorher haben wir also auch gezeigt, dass alle Umfangswinkel gleich groß sind. Diese Feststellung nennt man den Umfangswinkelsatz.
Alle Videos zum Thema
Videos zum Thema
Umfangswinkelsatz und Mittelpunktswinkelsatz (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Umfangswinkelsatz und Mittelpunktswinkelsatz (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



 Winkel am Kreis
Winkel am Kreis
 Umfangswinkelsatz und Mittelpunktswinkelsatz – Anwendung
Umfangswinkelsatz und Mittelpunktswinkelsatz – Anwendung









