Lokale Extrempunkte bei Funktionen mit mehreren Veränderlichen
Bei Funktionen mit einer Veränderlichen untersuchst du die erste Ableitung auf Nullstellen. Dies ist bei Funktionen mit mehreren Veränderlichen ähnlich.
Inhaltsverzeichnis zum Thema
- Was ist eine Funktion mit mehreren Veränderlichen?
- Lokale Extrempunkte
- Partielle Ableitungen
- Notwendige und hinreichende Bedingungen für lokale Extrema
Was ist eine Funktion mit mehreren Veränderlichen?
In der Schule lernst du Funktionen kennen, die von einer Variablen (oftmals $x$) abhängen.
Hier geht es um Funktionen, die von mehr als einer Variablen abhängen. Als Beispiel für eine Funktion mit mehreren Veränderlichen schauen wir uns die folgende Funktion an: $z=f(x,y)=x^2+y^2$.
Du siehst, dass diese Funktion von zwei Veränderlichen, nämlich $x$ und $y$, abhängt. So gelangst du zu einer Menge aus Punkten $(x|y|f(x,y))$, welche du in einem dreidimensionalen Koordinatensystem darstellen kannst. Du erhältst dann eine Kurve im Raum. Auch diese kann Extrema besitzen. Hier siehst du die Darstellung der oben gegebenen Funktion, ein Paraboloid:
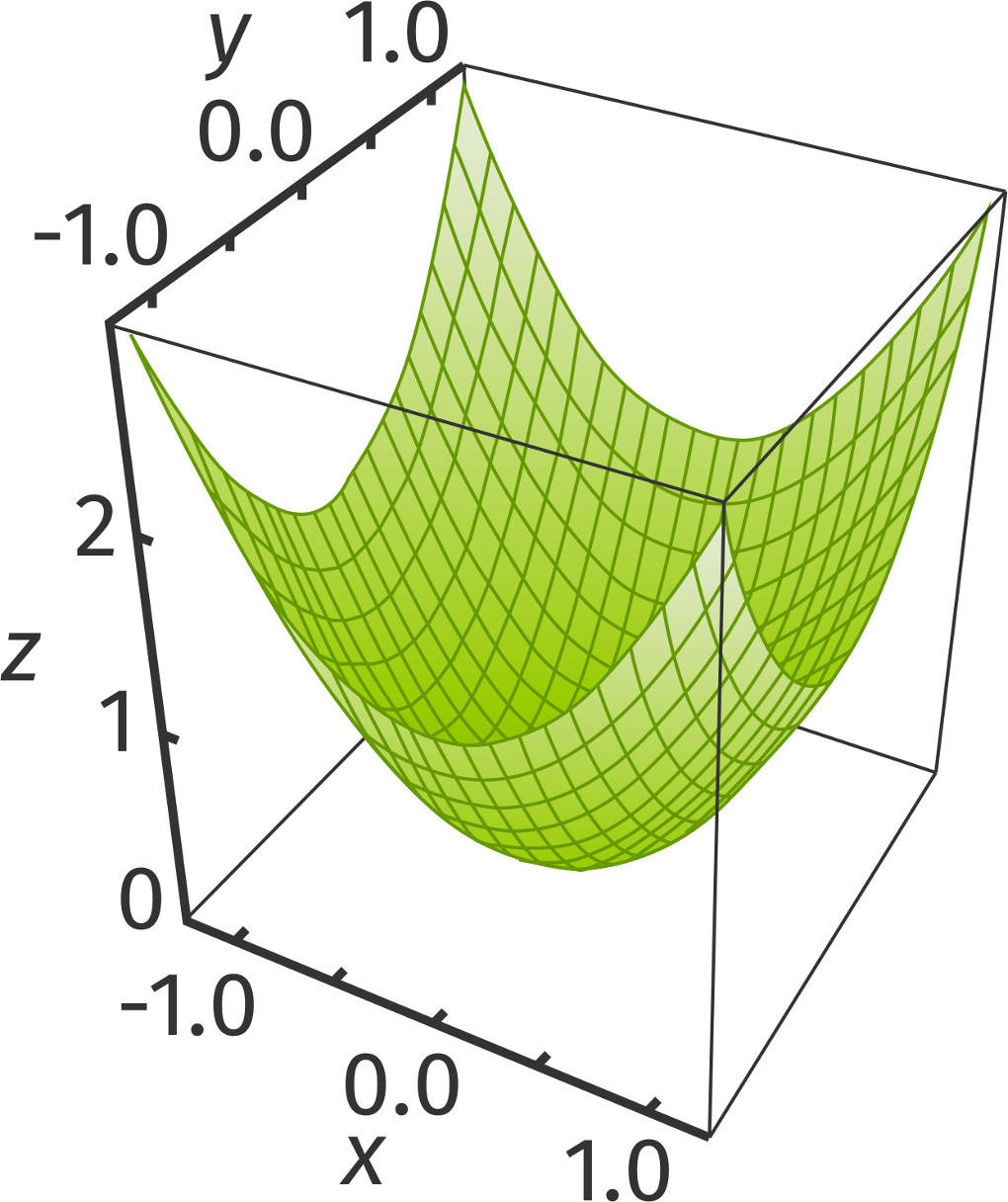
Wie du eine solche Funktion mit mehreren Veränderlichen auf Extrema untersuchst, erfährst du nun hier.
Lokale Extrempunkte
Erinnere dich nochmal daran, was du bei Funktionen mit einer Veränderlichen machen musst: Richtig, du benötigst die ersten beiden Ableitungen. Die erste Ableitung muss dann $0$ sein und die zweite Ableitung darf an den Stellen, an welchen die erste Ableitung $0$ wird, nicht $0$ sein.
Ebenso gehst du auch bei Funktionen mit mehreren Veränderlichen vor. Dabei sieht die erste Ableitung und auch die zweite ein wenig verändert aus. Man spricht in diesem Zusammenhang von partiellen Ableitungen.
Partielle Ableitungen
Ähnlich zu den Ableitungen bei Funktionen mit einer Veränderlichen bestimmst du die partiellen Ableitungen bei Funktionen mit mehreren Veränderlichen. Willst du zum Beispiel die erste partielle Ableitung nach $x$ bestimmen, betrachtest du die andere Veränderliche $y$ wie eine Konstante. So erhältst du:
$f_x=\frac{\partial f(x,y)}{\partial x}=2x$
Ebenso kannst du partiell nach $y$ ableiten:
$f_y=\frac{\partial f(x,y)}{\partial y}=2y$
$f_{x}$ sowie $f_{y}$ stehen dabei abkürzend für die entsprechenden partiellen Ableitungen.
Jede dieser beiden partiellen Ableitungen kannst du nochmal partiell ableiten und erhältst so die zweite partielle Ableitung. Diese wird häufig in Form einer Matrix, der sogenannten Hesse-Matrix, dargestellt:
$H_f=\begin{pmatrix} f_{xx}& f_{xy}\\ f_{yx}& f_{yy} \end{pmatrix}=\begin{pmatrix} 2&0 \\ 0&2 \end{pmatrix}$
Notwendige und hinreichende Bedingungen für lokale Extrema
So ähnlich wie bei Funktionen mit einer Veränderlichen sehen die Bedingungen für lokale Extrema bei Funktionen mit mehreren Veränderlichen aus:
- Es muss gelten, dass die ersten partiellen Ableitungen gleich $0$ sind. So erhältst du $x=0$ sowie $y=0$.
- An dieser Stelle $(0|0)$ muss die Determinante der Hesse-Matrix größer sein als $0$ und das Diagonalelement links oben, also $f_{xx}$, ungleich Null sein. Ist dieses Element größer als $0$, liegt ein lokales Minimum vor, andernfalls ein lokales Maximum. In den übrigen Fällen liegt ein Sattelpunkt vor.
Da die Hesse-Matrix eine Diagonalmatrix ist, erhältst du deren Determinante als Produkt der Diagonalelemente $\text{det}\left(H_{f}\right)=2\cdot 2=4\gt 0$. Zusätzlich ist $f_{xx}=2\gt 0$. Es liegt also ein lokales Minimum in $(0|0)$ vor. Der zugehörige Funktionswert ist $z=f(x,y)=0^2+0^2=0$.
Das lokale Minimum in dem Punkt $(0|0|0)$ kannst du in der obigen Abbildung erkennen.
Alle Videos zum Thema
Videos zum Thema
Lokale Extrempunkte bei Funktionen mit mehreren Veränderlichen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Lokale Extrempunkte bei Funktionen mit mehreren Veränderlichen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 Funktionen mit mehreren Veränderlichen – Lokale Extremwerte ohne Nebenbedingungen
Funktionen mit mehreren Veränderlichen – Lokale Extremwerte ohne Nebenbedingungen
 Funktionen mit mehreren Veränderlichen – Jacobi-Matrix und Hesse-Matrix
Funktionen mit mehreren Veränderlichen – Jacobi-Matrix und Hesse-Matrix









