Wechselstromkreis
Eigenschaften des Wechselstromkreis und Auswirkungen auf den ohmschen, kapazitiven und induktiven Widerstand in der Reihenschaltung und Parallelschaltung
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Wechselstrom im Alltag
Alle elektrischen Geräte funktionieren mit Strom. Dein Handy könntest du ohne seinen Akku nicht benutzen, auch Taschenlampen sind ohne Batterien wertlos, selbst Autos sind auf ihre Autobatterie angewiesen. All diesen Dingen ist es gemeinsam, dass sie mit Gleichstrom laufen, der von Akkus oder Batterien geliefert wird. Gleichstrom wird in der Schule recht früh behandelt, weil er das wichtigste vermittelt und mathematisch einfach ist. Für einen Großteil der elektrischen Geräte im Haushalt sind die dir bekannten Formeln des Gleichstroms allerdings nicht gültig. Der Kühlschrank, die Wasch- und Spülmaschine sowie der Fernseher und alle weiteren Geräte, die an einer Steckdose angeschlossen sind, beziehen aus dieser Wechselstrom.
Dass die Steckdose im Haushalt Wechselstrom liefert, hat verschiedene Gründe, wobei die entscheidenden wohl die sind, dass die Kraftwerke, die den Strom erzeugen, Generatoren verwenden und Generatoren erzeugen nun mal Wechselstrom. Zudem lässt sich Wechselstrom leichter übertragen als Gleichstrom.
Eigenschaften des Wechselstroms
Im Gegensatz zum Gleichstrom wird die elektrische Spannung beim Wechselstrom permanent umgepolt. Bei dem Strom aus der Steckdose geschieht dies beispielsweise 100 mal pro Sekunde, was einer Frequenz von $f=50\,$Hz entspricht. Durch das permanente Umpolen ist die Spannung nicht konstant sondern sinusförmig. Dasselbe gilt für den elektrischen Strom.
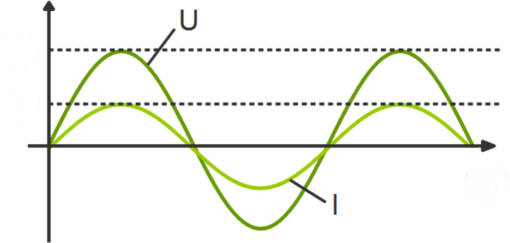
In einem Wechselstromkreis schwingen die Elektronen also nur hin und her statt sich gleichmäßig durch die Leitung zu bewegen.
$U(t)=U_\text{max}\sin(\omega t + \varphi_U) \,\text{und } I(t)=I_\text{max}\sin(\omega t + \varphi_I) $
Dabei ist $\omega$ die Kreisfrequenz $\omega=2\pi f$ und $\varphi$ die Phasenverschiebung. Ist die Phasenverschiebung des Stroms und der Spannung gleich groß ($\varphi_I=\varphi_U$), sagt man Strom und Spannung sind gleichphasig.
Effektivstromstärke und Effektivspannung
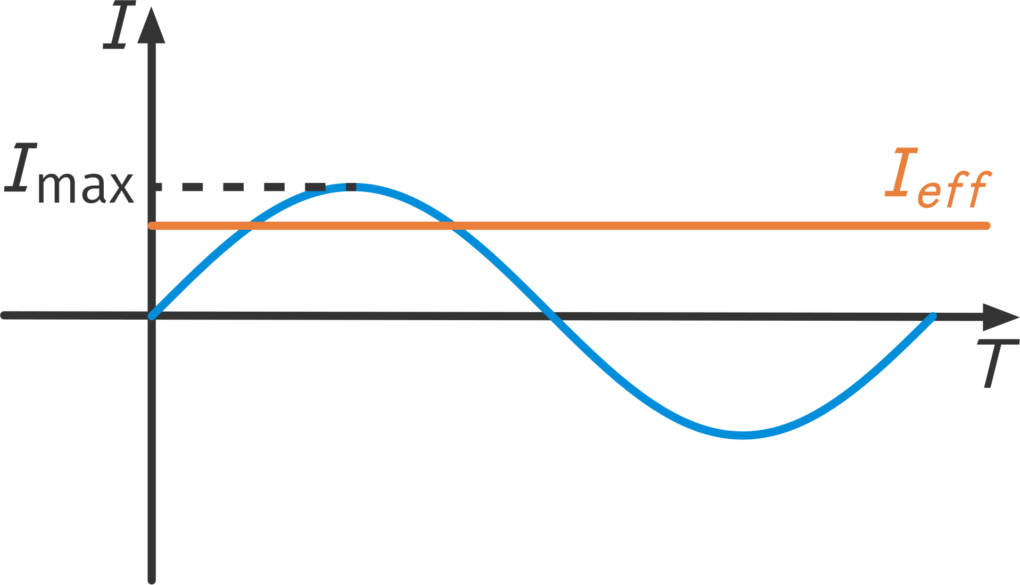
Schließt du ein Amperemeter an einen Wechselstromkreis an, so zeigt es dir einen bestimmten Wert an, obwohl sich die Stromstärke doch periodisch ändert. Dasselbe gilt für ein Voltmeter. Beide Geräte zeigen dir den effektiven Wert des Wechselstromkreises an, der auch zum Vergleich mit dem Gleichstromkreis genutzt werden kann. Die Effektivstromstärke $I_\text{eff}$ ist genau die Stromstärke, bei der in einem Gleichstromkreis, in dem diese Stromstärke fließt, dieselbe Leistung geliefert würde, wie im Wechselstromkreis. Anschaulich gesprochen bedeutet dies: Schließt du eine Glühlampe an einen Wechselstromkreis an (so wie jede Lampe in deinem Haus), so leuchtet diese genau so hell wie eine Lampe, die in einem Gleichstromkreis angeschlossen ist, in dem die effektive Stromstärke des Wechselstromkreises fließt. Man kann zeigen, dass Folgendes gilt:
$ I_\text{eff}=\dfrac{I_\text{max}}{\sqrt{2}} \,\text{und } U_\text{eff}=\dfrac{U_\text{max}}{\sqrt{2}}$.
Der Effektivwert der Spannung oder der Stromstärke ist der über eine Schwingungsdauer gemittelte quadratische Mittelwert.
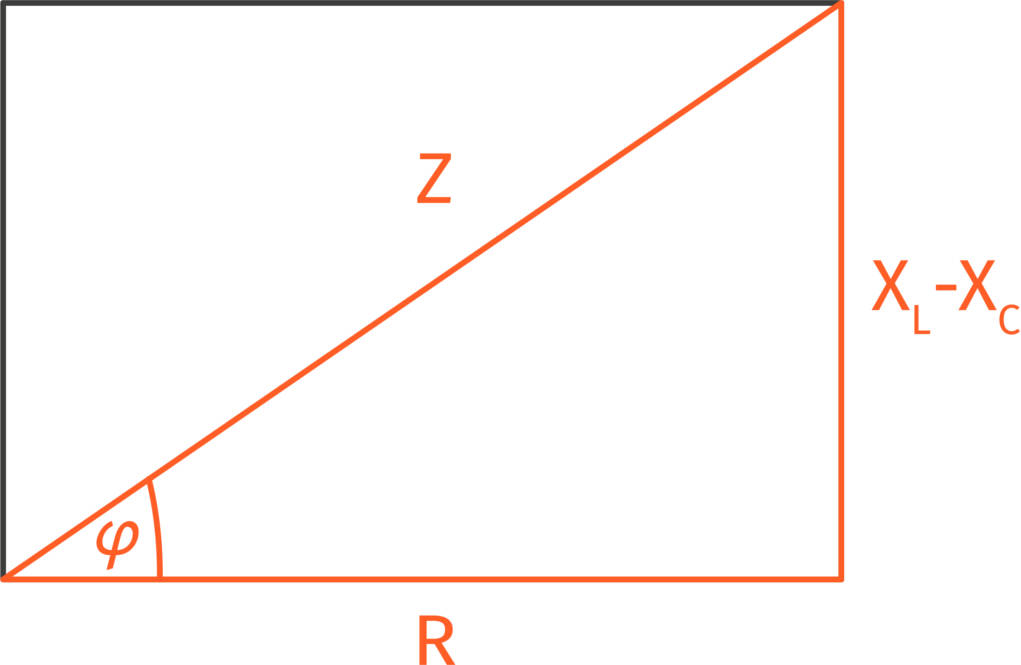
Der Widerstand eines Wechselstromkreises wird als Impedanz $Z$ bezeichnet und berechnet sich aus den Einzelwiderständen der Bauteile.
Widerstand von Kondensator und Spule
Da sich in einem Wechselstromkreis die Stromstärke und die Spannung ständig ändern, ergeben sich auch andere Verhaltensweisen am Kondensator oder der Spule im Vergleich zum Gleichstrom. Den Widerstand eines Wechselstromkreises oder eines Ohm'schen Verbrauchers (wie eine Glühbirne) kannst du wie gewohnt mit dem Ohm'schen Gesetz berechnen. Demnach fällt an der Glühlampe im Wechselstromkreis der Widerstand
$R=\dfrac{U_\text{eff}}{I_\text{eff}}$
ab und Strom und Spannung sind gleichphasig.
Kondensator
Baust du einen Stromkreis, der nur aus einer Gleichspannungsquelle und einem Kondensator mit Kapazität $C$ besteht, so wirst du feststellen, dass kein Strom fließt. Dies ist auch nicht verwunderlich, schließlich ist der Stromkreis durch den Abstand der Kondensatorplatten unterbrochen. Du könntest also sagen, dass der Kondensator einen unendlichen Widerstand hat, der verhindert, dass du Leistung abzapfen kannst. Im Wechselstromkreis ist dies anders, da die Elektronen hier schwingen und gar nicht fließen müssen. Man kann zeigen, dass der Widerstand eines Kondensators $X_C$ im Wechselstromkreis endlich ist.
$X_C=\dfrac{1}{2\pi f C}$
Das heißt, je größer die Frequenz des Stromkreises ist, desto kleiner ist der Widerstand des Kondensators. Ist die Frequenz hingegen Null (Gleichstrom) so ist der Widerstand tatsächlich unendlich. Außerdem eilt der Strom der Spannung um eine viertel Periode voraus, sodass beide nicht mehr gleichphasig sind. Dies kannst du dir in etwa so erklären, dass die schwingenden Elektronen zuerst am Kondensator sind und sich erst dann die Spannung an den Platten aufbauen kann.
Spule
Eine Spule ist nichts anderes als ein aufgewickelter Draht, der in der Physik als widerstandslos angenommen wird. Folglich hat eine Spule keinen elektrischen Widerstand. Auch hier gilt dies nur im Gleichstromkreis. Im Wechselstromkreis wird der Widerstand einer Spule $X_L$ größer als Null.
$ X_L=2\pi f L $
Du kannst hier erkennen, dass der Widerstand im Gleichstromkreis, also für $f=0\,$Hz, tatsächlich Null wird. In der Spule eilt die Spannung dem Strom um eine viertel Periode voraus.
Reihen- und Parallelschaltung
Stell dir vor, du müsstest nun die Impedanz (den Scheinwiderstand) einer komplexeren Schaltung berechnen, die sowohl Ohm'sche Verbraucher, Spulen und Kondensatoren enthält. Im Gleichstromkreis gibt es dafür eine einfache Rechenregel. Im Wechselstromkreis musst du allerdings berücksichtigen, dass Strom und Spannung an den Bauteilen nicht immer gleichphasig sind. Die Einzelwiderstände müssen daher vektoriell addiert werden. Dabei helfen dir Zeigerdiagramme, in denen du mit Pfeilen sowohl die Stärke als auch die Phasenverschiebung von Strom und Spannung darstellen kannst.
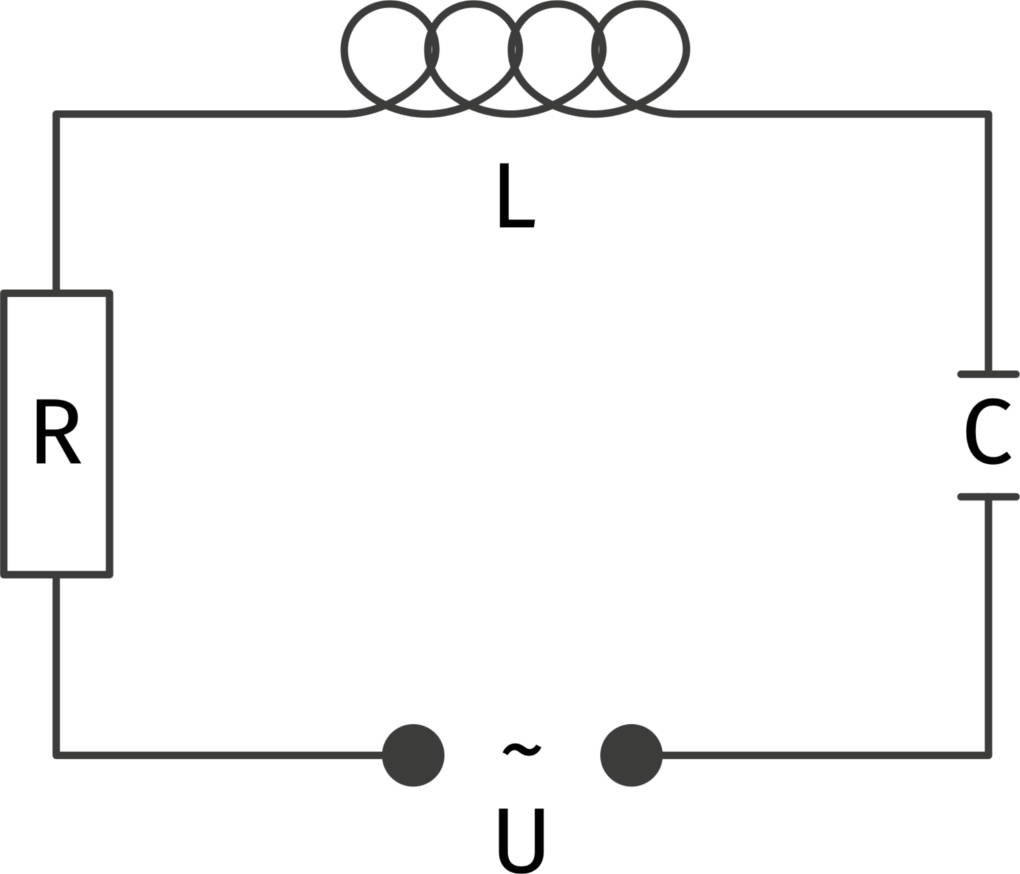
Reihenschaltung
Wie funktioniert die Reihenschaltung von Spule und Kondensator? In der Reihenschaltung ist die Stromstärke an jedem Bauteil gleich, weswegen die Stromstärke im Zeigerdiagramm als Orientierung verwendet wird. Wie oben beschrieben, eilt der Strom im Kondensator voraus und in der Spule hinterher, sodass sich für die Impedanz der Reihenschaltung folgende Formel ergibt:
$Z=\sqrt{R^2 + (X_L - X_C)^2}$.
Im Gleichstromkreis hätte eine einfach Addition der Einzelwiderstände genügt. Ein Sonderfall stellt die Resonanzfrequenz $f_0=\frac{1}{2\pi\sqrt{LC}}$, bei der die Impedanz am kleinsten und der Strom somit am größten wird. Eine Reihenschaltung wird deswegen auch Siebschaltung genannt, weil sie diese Frequenz heraussiebt.
Parallelschaltung
In der Parallelschaltung ist die Spannung an jedem Bauteil gleich und dient daher als Orientierung im Zeigerdiagramm. Im Gleichstromkreis müsstest du die Teilwiderstände invers addieren, um den inversen Gesamtwiderstand zu erhalten. Im Wechselstromkreis gilt hingegen:
$\dfrac{1}{Z}=\sqrt{\dfrac{1}{R^2} + (\dfrac{1}{X_C} - \dfrac{1}{X_L})^2}$.
Hier wird bei der Resonanzfrequenz die Impedanz der Schaltung besonders groß. Daher wird die Parallelschaltung auch als Sperrschaltung bezeichnet, da sie die Resonanzfrequenz sperrt.
Leistung
Wie ist die Leistung in einem Wechselstromkreis? Mit einem Wechselstromkreis lässt sich ebenso wie beim Gleichstrom elektrische Leistung transportieren und abgreifen. Wäre dies nicht so, würden die elektrischen Haushaltsgeräte, die an der Steckdose hängen, gar nicht funktionieren. Nun hast du aber gelernt, dass je nach verwendeten Bauteilen in einem Wechselstromkreis Strom und Spannung mit dem Winkel $\varphi$ phasenverschoben sein können. Dies hat Einfluss auf die Leistung, nämlich in der Art, dass nicht immer die gesamte Leistung genutzt werden kann (Wirkleistung), sondern auch ein Teil der Leistung geschluckt wird (Blindleistung), die dann nicht zur Verfügung steht. Allgemein gilt für die Wirkleistung in einem Wechselstromkreis:
$P_\text{Wirk}=U_\text{eff}\cdot I_\text{eff} \cdot \cos{\varphi}. $
Die Blindleistung berechnet sich mit dem Sinus. Für einen Ohm'schen Widerstand, bei dem Strom und Spannung gleichphasig ($\varphi=0$) sind, macht dies also keinen Unterschied im Vergleich zum Gleichstrom. Bei Spule und Kondensator hingegen, mit $\varphi=\frac{\pi}{2}$, lässt sich aber im Wechselstromkreis keine Leistung abzweigen, da sämtliche Leistung blind ist.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Wechselstromkreis (8 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Wechselstromkreis (9 Arbeitsblätter)
-
 Wechselstrom
PDF anzeigen
Wechselstrom
PDF anzeigen -
 Effektivwert von Wechselstrom und Wechselspannung
PDF anzeigen
Effektivwert von Wechselstrom und Wechselspannung
PDF anzeigen -
 Ohmscher Widerstand im Wechselstromkreis
PDF anzeigen
Ohmscher Widerstand im Wechselstromkreis
PDF anzeigen -
 Kondensator und kapazitiver Widerstand im Wechselstromkreis
PDF anzeigen
Kondensator und kapazitiver Widerstand im Wechselstromkreis
PDF anzeigen -
 Spule und induktiver Widerstand im Wechselstromkreis
PDF anzeigen
Spule und induktiver Widerstand im Wechselstromkreis
PDF anzeigen -
 Wechselstromwiderstand
PDF anzeigen
Wechselstromwiderstand
PDF anzeigen -
 Leistung im Wechselstromkreis
PDF anzeigen
Leistung im Wechselstromkreis
PDF anzeigen -
 Reihen- und Parallelschaltungen im Wechselstromkreis
PDF anzeigen
Reihen- und Parallelschaltungen im Wechselstromkreis
PDF anzeigen -
 Parallelschaltung von Spule, Kondensator und Ohm'schen Widerstand
PDF anzeigen
Parallelschaltung von Spule, Kondensator und Ohm'schen Widerstand
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie





















