Wahrscheinlichkeitsfunktion, Dichtefunktion und Verteilungsfunktion
Wertetabelle, Zufallsexperiment, Aufsummieren
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Definition einer Wahrscheinlichkeit
- Was ist eine Wahrscheinlichkeitsfunktion?
- Was ist eine Verteilungsfunktion?
- Dichtefunktion und Verteilungsfunktion am Beispiel einer stetigen Wahrscheinlichkeitsverteilung
- Was ist eine Dichtefunktion?
- Die Verteilungsfunktion einer stetigen Wahrscheinlichkeitsverteilung
- Beispiel
Definition einer Wahrscheinlichkeit
Betrachte hierfür als Zufallsexperiment das Werfen eines Spielwürfels. Das zugehörige Netz siehst du hier:
Die Ergebnismenge ist bei der beobachteten Größe „Augenzahl“ gegeben durch $\Omega=\{1;2;3;4;5;6\}$. Ein Ereignis ist eine beliebige Teilmenge der Ergebnismenge.
Eine Wahrscheinlichkeitszuordnung ist eine Zuordnung, die jedem Ereignis $A\subseteq \Omega$ eine reelle Zahl zuordnet. Dabei müssen die folgenden Bedingungen, die Kolmogorov-Axiome, erfüllt sein:
- $P(A)\ge 0$ für jedes Ereignis $A$.
- $P(\Omega)=1$, das sichere Ereignis. Dies wird als Normiertheit bezeichnet.
- $P(A\cup B)=P(A)+P(B)$, sofern $A\cap B=\emptyset$. Dies ist der Additionssatz.
Es gelten die folgenden Eigenschaften:
- $P(A)\le 1$
- $P(\emptyset)=0$, das unmögliche Ereignis,
- $P(\bar A)=1-P(A)$, das Gegenereignis,
- $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
- $A\subseteq B$ dann gilt $P(A)\le P(B)$
- $P(A)=P(e_1)+...+P(e_n)$, wobei $A=\{e_1;...;e_n\}$ ist.
Was ist eine Wahrscheinlichkeitsfunktion?
Sei $X$ eine Zufallsgröße, dann kann man mit Hilfe dieser eine Wahrscheinlichkeitsfunktion $f(X=x_{i})$ für diese Zufallsgröße definieren. Diese Funktion ordnet jedem Wert, den die Zufallsgröße annehmen kann, die entsprechende Wahrscheinlichkeit für das Eintreten dieses Wertes zu. Es wird also eine reelle Zahl zwischen 0 und 1 zugeordnet. Die Wahrscheinlichkeitsfunktion für das Werfen des obigen Würfels ist wie folgt gegeben:
$\quad~~~f(x)= \begin{cases} \frac16 & \text{, wenn }x\in \{1;...;6\} \\ 0 & \text{, sonst } \end{cases}$
Hier siehst du den Graphen dieser Funktion
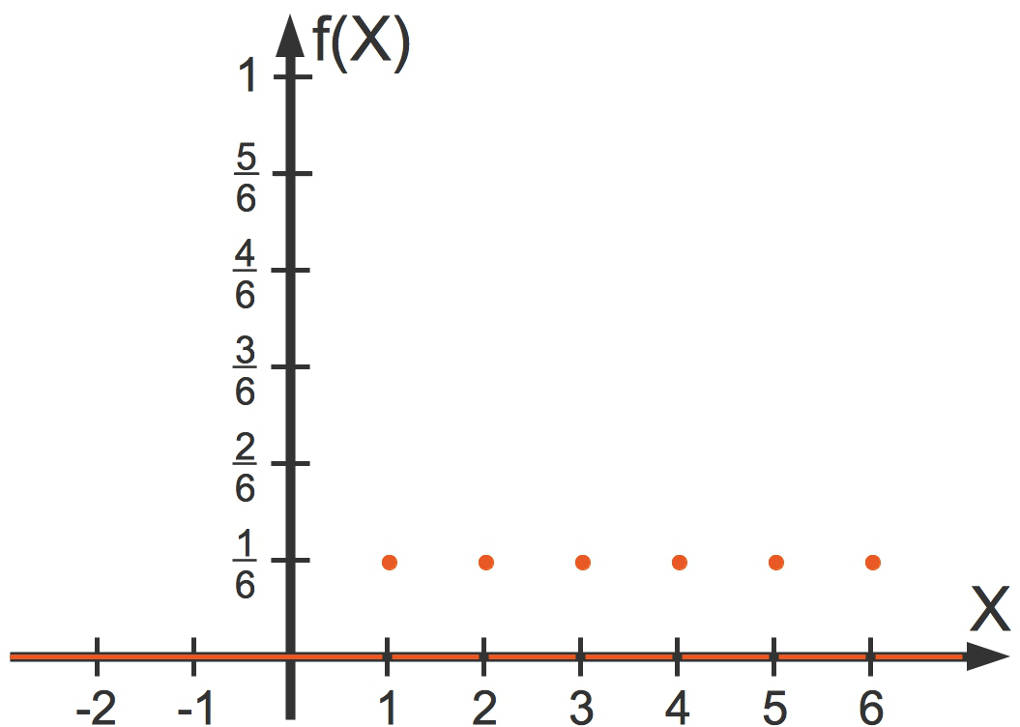
Da die Wahrscheinlichkeiten nur für endlich viele Ausprägungen $x\in\{1;...;6\}$ der Zufallsgröße ungleich $0$ ist, spricht man von einer diskreten Wahrscheinlichkeitsfunktion. Andernfalls liegt eine stetige Wahrscheinlichkeitsfunktion vor.
Was ist eine Verteilungsfunktion?
Zu dieser Wahrscheinlichkeitsfunktion ist eine Verteilungsfunktion $F(x)=P(X\le x)$ als Summe aller Wahrscheinlichkeiten der Ausprägungen kleiner oder gleich $x$ gegeben. Diese Wahrscheinlichkeit wird auch als kumulierte oder summierte Wahrscheinlichkeit bezeichnet.
Für das obige Beispiel des Wurfes eines regulären Würfels ist beispielsweise der Wert der Verteilungsfunktion für $F(5)$ mit $F(x)=P(X\le x)$ gegeben durch:
$F(5)=P(X\le 5)=P(X=1)+...+P(X=5)=\frac56$.
Den Verlauf der Verteilungsfunktion zu dem obigen Beispiel kannst du hier sehen:
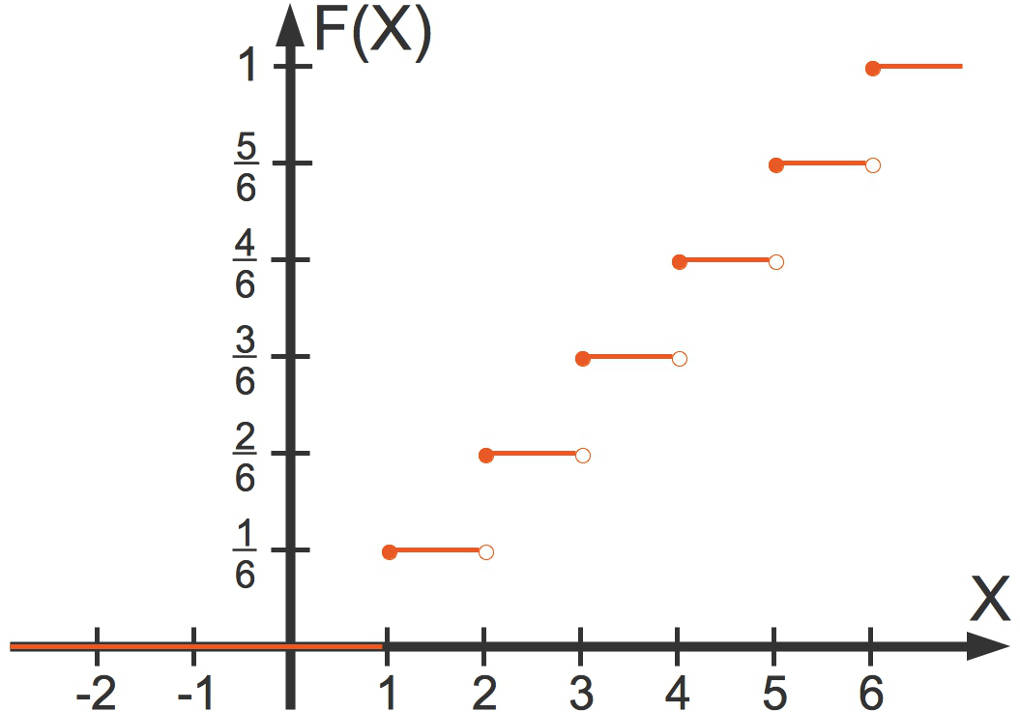
Der Wert für $F(1)=P(X \le 1)$ ist $\frac{1}{6}$. Bis zur nächsten möglichen Ausprägung ($X=2$) bleibt die Wahrscheinlichkeit bei $\frac{1}{6}$, da es zwischen den Ausprägungen $X=1$ und $X=2$ keine Werte gibt, denn es liegt eine diskrete Wahrscheinlichkeitsfunktion zugrunde. Ab der Ausprägung $X=2$ beträgt der Wert der Verteilungsfunktion $\frac{2}{6}=\frac{1}{3}$, denn es gilt:
$F(2)=P(X \le 2) = P(X=1) + P(X=2) = \frac{1}{6} + \frac{1}{6} =\frac{2}{6} =\frac{1}{3}$.
Ein weiteres Beispiel für eine diskrete Wahrscheinlichkeitsverteilung ist die Binomialverteilung.
Dichtefunktion und Verteilungsfunktion am Beispiel einer stetigen Wahrscheinlichkeitsverteilung
Wenn die Wahrscheinlichkeiten von unendlich vielen Ausprägungen der Zufallsgröße $X$ ungleich $0$ sind, liegt eine stetige Wahrscheinlichkeitsverteilung vor.
Was ist eine Dichtefunktion?
Bei Verteilungen kann eine Dichtefunktion angegeben werden. Diese Dichtefunktion wird mit $f(x)$ bezeichnet. Sie entspricht bei einer stetigen Verteilung der Wahrscheinlichkeitsfunktion bei diskreten Wahrscheinlichkeitsverteilungen.
Allerdings kann die Dichtefunktion auch Funktionswerte größer als $1$ haben. Dies ist bei einer Wahrscheinlichkeit nicht möglich. Das bedeutet, dass die Funktionswerte einer Dichtefunktion nicht gleichzusetzen sind mit einer Wahrscheinlichkeit.
Es gilt
$\quad~~~\int\limits_{-\infty}^{+\infty}~f(t)~dt=1$.
Dies entspricht der Eigenschaft, dass $P(\Omega)=1$ ist.
Die Verteilungsfunktion einer stetigen Wahrscheinlichkeitsverteilung
Im Falle einer stetigen Wahrscheinlichkeitsverteilung erhältst du die zugehörige Verteilungsfunktion durch Integration der Dichtefunktion
$\quad~~~F(x)=\int\limits_{-\infty}^x~f(t)~dt$.
Beispiel
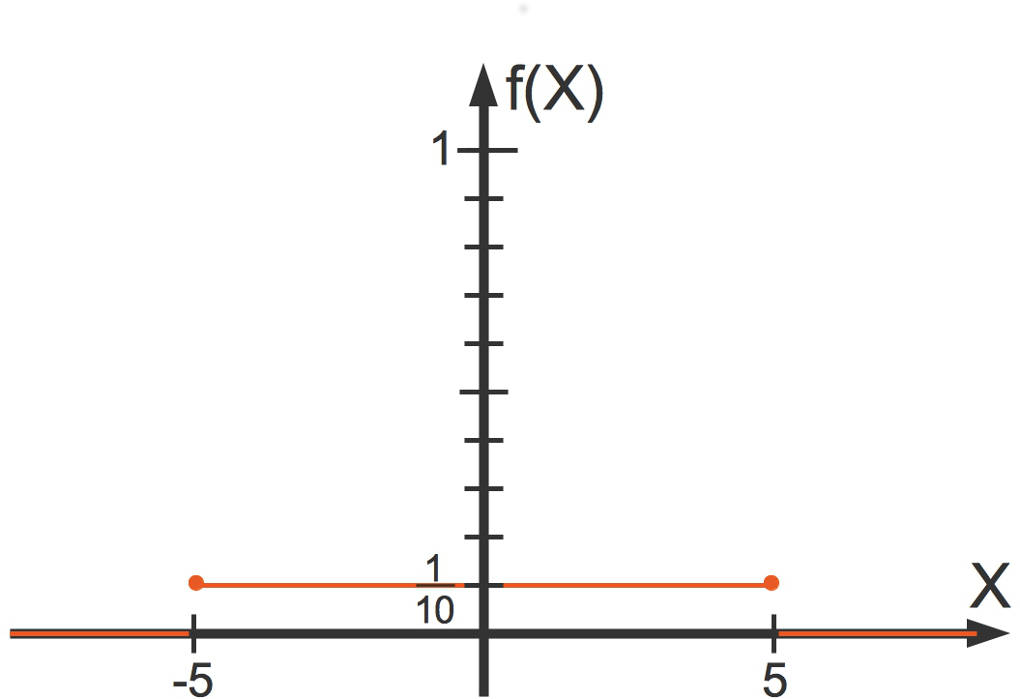
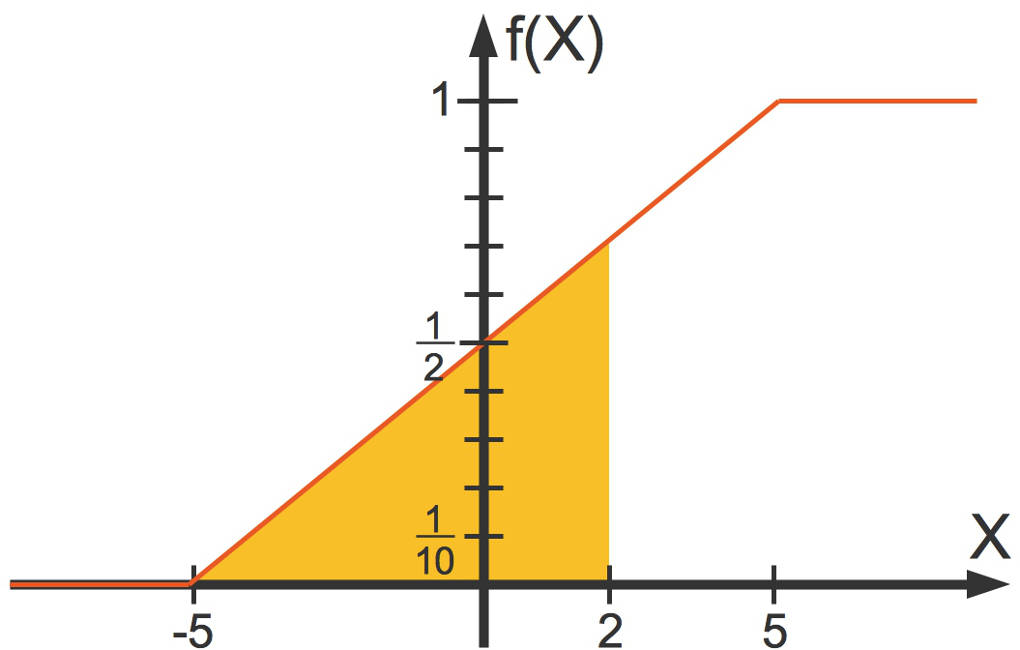
Paul möchte morgens immer um 7:30 Uhr an der Bushaltestelle sein. Manchmal ist er früher und manchmal später an der Bushaltestelle. Die Dichtefunktion für seine Ankunftszeit sei gegeben durch
Die Dichtefunktion sei gegeben durch
$\quad~~~f(x)= \begin{cases} \frac1{10} \text{, für }-5\le x\le 5 \\ 0\text{, sonst } \end{cases}$
Dabei ist $x$ die Anzahl der Minuten, die Paul zu früh (negatives $x$) oder zu spät (positives $x$) kommt. Hier kannst du die Dichtefunktion sehen:
Die Verteilungsfunktion ist wie folgt gegeben
$\quad~~~F(x)= \begin{cases} 0 & \text{, für } -\infty \leq x \leq -5\\ \frac{1}{10}(5+x) & \text{, für } -5 \le x \leq 5 \\ 1 & \text{, für } x>5 \end{cases}$
Wenn Pauls Bus nun um 7:32 abfährt, ist die Wahrscheinlichkeit dafür, dass Paul den Bus erreicht gegeben durch $P(x\le 2)=F(2)=0,1\cdot (5+2)=0,7$. Dies kannst du anschaulich hier sehen.
Ein Beispiel für eine stetige Wahrscheinlichkeitsverteilung ist die Normalverteilung. Die zugehörige Dichtefunktion entspricht der (Gauß'sche) Glockenkurve.
Alle Lerntexte zum Thema
Lerntexte zum Thema
Wahrscheinlichkeitsfunktion, Dichtefunktion und Verteilungsfunktion (1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Wahrscheinlichkeitsfunktion, Dichtefunktion und Verteilungsfunktion (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung

 Wahrscheinlichkeitsfunktion und Verteilungsfunktion einer diskreten Zufallsgröße
Wahrscheinlichkeitsfunktion und Verteilungsfunktion einer diskreten Zufallsgröße









