Was ist eine Wurzelfunktion?


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Was ist eine Wurzelfunktion?
In der Mathematik spielen Funktionen eine ganz entscheidende Rolle. Es gibt viele unterschiedliche Arten von Funktionen. Du hast mit Sicherheit schon etwas von der Potenzfunktion gehört. Was passiert aber, wenn du zu einem bestimmten y-Wert den passenden x-Wert bei einer Potenzfunktion bestimmen willst? In diesem Video lernst du kennen, wie du dafür die Umkehrfunktion der Potenzfunktion, nämlich die Wurzelfunktion, anwenden kannst.
Transkript Was ist eine Wurzelfunktion?
Hallo und herzlich Willkommen zu meinen Video, in dem wir die Frage klären wollen, was denn eigentlich eine Wurzelfunktion ist. Schauen wir uns dazu einen Eiswürfel an. Es gibt unterschiedlich große Eiswürfel, weshalb die Länge einer Seite variiert. Wir bezeichnen diese also mit x. Das Volumen eines Eiswürfels ist in Abhängigkeit von der Seitenlänge x ebenfalls unterschiedlich groß. Es ergibt sich aus V(x)=x3. Die Seitenlänge x ist natürlich größer oder gleich Null. Daher ist auch x3 größer oder gleich Null.
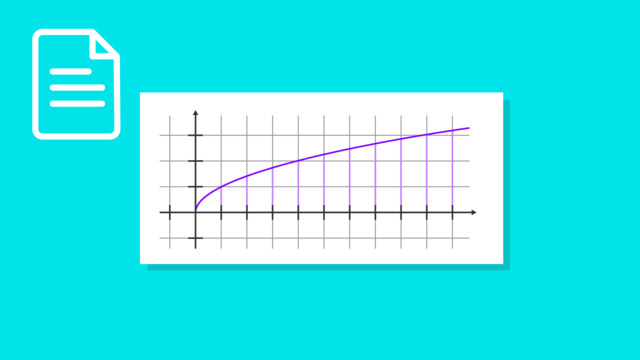
In einem Koordinatensystem, in dem das Volumen V in cm3 in Abhängigkeit von der Seitenlänge x in cm dargestellt wird, ergibt sich folgender Graph. Dies ist der Graph einer Potenzfunktion dritten Grades.
Wenn wir nun ein bestimmtes Volumen, z. B. 8cm3, gegeben haben und ablesen wollen, wie lang dann x sein muss, ist es auch möglich, die Seitenlänge x in Abhängigkeit vom Volumen V darzustellen. Dafür vertauschen wir die x- und y-Achse: Aus x in cm wird nun V in cm3 und aus V in cm3 wird x in cm. Der Graph verändert sich dann so, dass er an der Ursprungsgeraden t mit t(x)=x gespiegelt wird. Wichtig dabei ist, dass x größer gleich Null ist. Bei dem dargestellten Graphen handelt es sich nun um eine Wurzelfunktion.
Wir wollen die graphische Veranschaulichung nun verallgemeinern und formalisieren. Für die Potenzfunktion f(x)=xn sei x eine beliebige reelle Zahl, die größer oder gleich Null ist. Zudem ist n eine natürliche Zahl, die ungleich 0 ist. Wegen x größer gleich Null, ist auch xn größer oder gleich Null. Außerdem tritt kein Funktionswert doppelt auf. Daher existiert eine Umkehrfunktion g, sodass g(xn)=x ist. Setzt man nun xn=y, dann ist x=n-te Wurzel aus (y) wegen x≥0 äquivalent dazu. Also ist g(y)=n-te Wurzel aus (y). Bezeichnen wir die unabhängige Größe noch wie üblich mit x, dann ergibt sich g(x)=n-te Wurzel aus (x) als Umkehrfunktion einer Potenzfunktion n-ten Grades. Dies ist dann eine Wurzelfunktion.
Schauen wir uns ein paar Eigenschaften der Wurzelfunktion an. Dazu zeichnen wir drei Wurzelfunktionen mit unterschiedlichen natürlichen Zahlen n in ein Koordinatensystem ein. Einmal für n=2, n=3 und n=5. Der Definitions- und Wertebereich besteht aus allen positiven reellen Zahlen. Es ist weiterhin g(0)=n-te Wurzel aus 0=0 und g(1)=n-te Wurzel aus 1=1 für alle natürlichen Zahlen n. Damit sind P1=(0|0) und P2=(1|1) besondere Punkte einer Wurzelfunktion. Außerdem folgt, dass x=0 eine Nullstelle ist. Die Wurzelfunktion ist zudem eine monoton steigende Funktion.
Fassen wir noch einmal zusammen: Die Potenzfunktion f(x)= xn mit der natürlichen Zahl n und n ungleich 0, besitzt mit der Einschränkung für x aus dem Bereich der positiven reellen Zahlen mit der Null eine Umkehrfunktion g. g heißt Wurzelfunktion mit der Funktionsgleichung g(x)=n-te Wurzel aus x. Der Definitions- und Wertebereich von g besteht aus der Menge der positiven reellen Zahlen mit der Null . Die Punkte P1=(0|0) und P2=(1|1) sind besondere Punkte von g. Der Graph der Wurzelfunktion g ist außerdem monoton steigend. Beide Eigenschaften sind unabhängig von n. Das war‘s von mir. Ich danke dir für‘s Zuschauen und bis zum nächsten Mal.
Was ist eine Wurzelfunktion? Übung
-
Ergänze die Erklärung zur Wurzelfunktion.
TippsHier ist der Graph der Funktion $f(x)=x^2$ für den Definitionsbereich $\mathbb{D} = \mathbb{R}_0^{+}$ zu sehen.
Die Menge $ \mathbb{R}_0^{+}$ lässt sich auch anders darstellen:
$\{x \in \mathbb{R} | x \ge 0\}$
Dabei steht im rechten Teil die Einschränkung der reellen Zahlen auf die positiven reellen Zahlen.
Hier ist der Graph der Funktion $f(x)=\sqrt x$ zu sehen. Weil aus einer negativen Zahl keine Wurzel gezogen werden kann, muss der Definitionsbereich für die Funktion $\mathbb{D} = \mathbb{R}_0^{+}$ lauten.
Die Spiegelungsgerade $f(x)=x$, welche durch den Koordinatenursprung verläuft, wird auch als 1. Winkelhalbierende bezeichnet.
LösungWas ist eine Wurzelfunktion?
Wenn man einen Würfel mit der Seitenlänge $x\ge0$ betrachtet, hat dieser das Volumen
$V(x)=x^3$.
Dieses Volumen kann man in einem Koordinatensystem darstellen.
Will man nun umgekehrt wissen, für welches $x$ das Volumen zum Beispiel $8~cm^3$ beträgt, kann man den Graphen der Umkehrfunktion betrachten. Dieser ergibt sich durch Vertauschen von $x$ und $V$ bei der Beschriftung des Koordinatensystems. Dann wird der Graph der Potenzfunktion an der Ursprungsgerade $t(V)=V$ gespiegelt.
Der so erhaltene Graph ist der Graph einer Wurzelfunktion.
-
Gib die Eigenschaften der Wurzelfunktionen an.
TippsHier siehst du den Graphen der Funktion $f(x)=\sqrt x$.
Beachte, dass für umkehrbare Funktionen gilt:
Ist der Graph der Funktion steigend (fallend), dann ist auch der Graph der Umkehrfunktion steigend (fallend).
Überlege dir, ob es ein $x$ gibt, so dass $x^n=0$ ist.
LösungSei $f(x)=x^n$ eine Potenzfunktion, dabei ist $x\ge 0$ und $n\in\mathbb{N}$ sowie $n\neq 0$.
Dann besitzt diese Funktion eine Umkehrfunktion, da kein Funktionswert mehr als einmal vorkommt.
Die Umkehrfunktion einer Potenzfunktion wird als Wurzelfunktion bezeichnet.
Für diese gilt $\mathbb{D}=\mathbb{W}=\mathbb{R}^+_0$.
- Es ist $g(0)=0$ und $g(1)=1$. Dies ist unabhängig von dem Wurzelexponenten $n$.
- Das bedeutet, dass die Punkte $P_0(0|0)$ sowie $P_1(1|1)$ auf jedem Graphen der Wurzelfunktion unabhängig von $n$ liegen.
-
Ermittle die Umkehrfunktion.
TippsGanz allgemein ist durch $\sqrt[n] x$ die Umkehrfunktion zu $x^n$ gegeben.
$n$ ist der sogenannte Wurzelexponent.
Dies stellt den Zusammenhang zu $x^n$ dar. $n$ wird als Exponent bezeichnet.
$\sqrt x$ ist die Quadratwurzel. Der Wurzelexponent $2$ wird weggelassen.
LösungGanz allgemein gilt, dass die n-te Wurzel die Potenz mit dem Exponenten $n$ umkehrt.
Sei also $f(x)=x^n$, mit $x\ge 0$ und $n\in\mathbb{N}\setminus\{0\}$, dann ist die Umkehrfunktion
$g(x)=\sqrt[n] x$.
$n$ wird als der Wurzelexponent bezeichnet.
$\begin{array}{c|c} \text{Funktion}&\text{Umkehrfunktion}\\ \hline x^2&\sqrt x\\ \hline x^3&\sqrt[3] x\\ \hline x^4&\sqrt[4] x\\ \hline x^5&\sqrt[5] x\\ \hline ...&... \end{array}$
Ein Sonderfall ist die Quadratwurzel, die Umkehrung von $x^2$. Bei dieser wird der Wurzelexponent nicht aufgeschrieben.
-
Berechne verschiedene Werte von Wurzelfunktionen.
TippsDu kannst jede der Aufgaben ohne den Taschenrechner lösen.
Da $2^6=64$ ist, ist umgekehrt $\sqrt[6] {64}=2$.
Alle Lösungen sind natürliche Zahlen.
LösungAlle Lösungen stehen hier. Man muss dafür nur wissen, dass die n-te Wurzel die Umkehrung von der n-ten Potenz ist.
- Da $2^5=32$ ist, ist umgekehrt $\sqrt[5]{32}=2$.
- Da $3^4=81$ ist, ist umgekehrt $\sqrt[4]{81}=3$.
- Da $5^2=25$ ist, ist umgekehrt $\sqrt{25}=5$.
- Da $4^3=64$ ist, ist umgekehrt $\sqrt[3]{64}=4$.
- Da $5^3=125$ ist, ist umgekehrt $\sqrt[3]{125}=5$.
-
Bestimme die Wurzelfunktion.
TippsEin Term der Form $a^b$ heißt Potenz. Dabei ist $a>0$ die Basis und $b$ der Exponent.
Ein Term der Form $\frac ab$ ist ein Bruch.
Ein Term der Form $a\cdot b$ ist ein Produkt.
LösungDies ist eine Wurzelfunktion. Dabei gibt die Zahl $n$ an, welche Wurzel gezogen wird. Sie wird als Wurzelexponent bezeichnet.
Sei zum Beispiel $f(x)=x^5$, dann ist $g(x)=\sqrt[5] x$ die Umkehrfunktion dieser Funktion. Dies ist die fünfte Wurzel.
Übrigens: Bei der zweiten Wurzel $\sqrt[2]{x}$ lässt man den Wurzelexponenten weg: $\sqrt{x}$. Diese Wurzel wird als Quadratwurzel bezeichnet.
-
Leite die fehlenden Größen her.
TippsStelle jeweils mit der Volumen- oder Flächenformel eine Gleichung auf und löse diese nach der unbekannten Größe.
Verwende die folgenden Formeln:
- Kugel-Volumen: $V(r)=\frac43~\pi~r^3$
- Kreis-Fläche: $A(r)=\pi~r^2$
- Würfel-Volumen: $V(x)=x^3$
- Quadrat-Fläche: $A(x)=x^2$
Sei zum Beispiel das Volumen einer Kugel bekannt: $V=800$. Dann ist die folgende Gleichung zu lösen:
$800=\frac43~\pi~r^3$.
Dividiere zunächst durch $\frac43~\pi$ und ziehe dann die dritte Wurzel.
LösungEs muss jeweils die entsprechende Formel aufgestellt und der bekannte Wert eingesetzt werden, dann wird die Gleichung nach der unbekannten Größe aufgelöst.
Schauen wir uns zunächst den Würfel an. Das Volumen eines Würfels lässt sich mit $V=x^3$ berechnen:
$\begin{array}{rclll} x^3&=&64000&|&\sqrt[3]{~~~}\\ x&=&40 \end{array}$
Die Seite ist $40~cm$ lang.
Der Flächeninhalt eines Quadrats lässt sich mit $A=x^2$ berechnen:
$\begin{array}{rclll} x^2&=&156,25&|&\sqrt{~~~}\\ x&=&12,5 \end{array}$
Die Seite ist $12,5~m$ lang.
Der Flächeninhalt eines Kreises wird durch $A=\pi~r^2$ berechnet:
$\begin{array}{rclll} \pi~r^2&=&320&|& : \pi\\ r^2&\approx&101,86&|&\sqrt{~~~}\\ r&\approx&10,1 \end{array}$
Der Radius beträgt ungefähr $10,1~dm$.
Das Volumen einer Kugel kann mit $V=\frac43 ~\pi~r^3$ berechnet werden:
$\begin{array}{rclll} \frac43~\pi~r^3&=&72,5&|&:\left(\frac43~\pi\right)\\ r^3&\approx&17,31&|&\sqrt[3]{~~~}\\ r&\approx&2,6 \end{array}$
Der Radius der Kugel beträgt ungefähr $2,6~m$.
9.859
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?










Die Graphen sind m.E. falsch
für 0 < x<1 ist die Quadratwurzel kleiner als die 3. Wurzel und...