Streifenmethode des Archimedes

Streifenmethode des Archimedes Übung

• Ordne der Skizze die passenden Angaben zu.

  Tipps

  Die Fläche A unter dem Graphen ist die Fläche, die von der $x$-Achse und dem Graphen der Funktion $f(x)$ im Intervall $[0;1]$ eingeschlossen wird.

  Die Obersumme orientiert sich immer am höchsten $f(x)$-Wert im jeweiligen Streifen.

  Lösung

  Beginne immer mit den Angaben, bei denen du dir sicher bist:

  Den Graphen der Funktion kannst du sicherlich schnell zuordnen. Hier musst du nur genau hinschauen, um welche Funktion es sich handelt.

  Die Intervallgrenzen im Intervall $[0;1]$ kannst du sicherlich auch leicht erkennen: Das bedeutet, dass $x=0$ die untere Intervallgrenze ist und $x=1$ die obere Intervallgrenze.

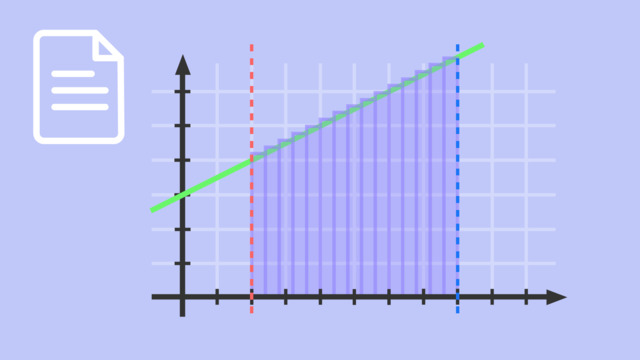
  Die Fläche $A$ unter dem Graphen ist die Fläche, die von der $x$-Achse und dem Graphen der Funktion $f(x)$ im Intervall $[0;1]$ eingeschlossen wird, also die schraffierte Fläche.

  Da die Fläche, die die grünen Säulen beschreiben, größer ist als die schraffierte Fläche $A$, handelt es sich hier um die Obersumme.

  Die Obersumme orientiert sich immer am höchsten $f(x)$-Wert im jeweiligen Streifen. Insofern ist der $f(x)$-Wert, der durch die grüne gestrichelte Linie hervorgehoben ist, der Wert für $f(0,6)$. Tipp: Orientiere dich am Graphen, nicht an den Säulen, dann erkennst du sofort, zu welchem $x$-Wert der $f(x)$-Wert gehört.

• Gib die Formeln zur Berechnung der Obersumme und der Untersumme an.

  Tipps

  Lies die Angaben genau und in Ruhe.

  Am Nenner des Bruchs erkennst du die Streifenzahl.

  Bei der Obersumme entspricht der letzte Term der Formel der Anzahl der Streifen.

  Der letzte Term der Untersummenformel ist um eins kleiner als die Streifenanzahl.

  Lösung

  Um diese Aufgabe lösen zu können, schaust du dir die Angaben zunächst ganz genau an. Es gibt die Unterscheidung nach Ober- und Untersumme und verschiedene Streifenanzahlen: $5$, $10$ und $n$.

  Der Nenner des Bruchs entspricht immer der Streifenzahl. Damit kannst du zumindest schon einmal die Formel zuordnen, bei der $5$ Streifen verwendet wurden.

  Die Obersumme berechnest du immer, indem du in der Klammer mit den Summen alle natürliche Zahlen von $1$ bis zur Streifenanzahl erst quadrierst und dann addierst. Die letzte Zahl gibt dir also Aufschluss, ob es sich um die Ober- oder Untersumme handelt: Bei der Berechnung der Obersumme entspricht sie der Anzahl der Streifen, bei der Berechnung der Untersumme entspricht sie der Anzahl der Streifen minus $1$.

  Wenn du alle Informationen kombinierst, kannst du die Formeln den Beschreibungen ganz eindeutig zuordnen.

• Berechne die Ober- und Untersumme zur Funktion $f$.

  Tipps

  Du kannst die allgemeinen Formeln für Ober- und Untersumme anwenden.

  Hier ist $n=10$.

  Lösung

  Diese Aufgabe kannst du sehr schnell mit den allgemeinen Formeln für die Funktionsgleichung $f(x)=x^2$ im Intervall [0;1] lösen:

  $O_n=(\frac{1}{n})^3\cdot (1^2+2^2+...+n^2)$

  $U_n=(\frac{1}{n})^3\cdot (0^2+1^2+...+(n-1)^2)$.

  Wenn du für die Streifenanzahl $n$ den Wert $10$ einsetzt, ergibt sich:

  $O_{10}=(\frac{1}{10})^3\cdot (1^2+2^2+...+10^2)=0,385~FE$

  $U_{10}=(\frac{1}{10})^3\cdot [0^2+1^2+...+(9)^2)=0,285~FE$.

  Die allgemeinen Formeln aus dem Video kannst du immer dann anwenden, wenn es sich um die Funktion mit der Gleichung $f(x)=x^2$ und das Intervall $[0;1]$ handelt.

  Für eine andere Funktion und/oder ein anderes Intervall musst du die Formeln mit Hilfe von Überlegungen wie im Video zunächst herleiten.

• Berechne die Fläche unter dem Graphen näherungsweise mit Hilfe der Streifenmethode.

  Tipps

  Lies die Aufgaben genau und in Ruhe und schaue, welche Angaben darin vorkommen.

  Die Streifenbreite ist immer Intervallbreite geteilt durch Streifenanzahl.

  Die Breite des Intervalls $[1;2]$ beträgt $1$.

  Durch das veränderte Intervall verändern sich auch die Formeln zur Berechnung von Ober- und Untersumme.

  Lösung

  Gegeben sind die Funktion $f(x)=x^2$, das Intervall $[1;2]$ sowie die Streifenanzahl von zehn Streifen.

  Gesucht ist die Fläche, die der Graph $f(x)$ und die $x$-Achse im Intervall $[1;2]$ einschließen.

  Das Intervall hat die Breite von $1$ bis $2$, also eine Breite von $1$. Die zehn Streifen haben also jeweils eine Breite von $\frac{1}{10}$.

  Die Formel für die Obersumme lässt sich nun so herleiten:

  $O_{10}=\frac{1}{10}\cdot (f(\frac{11}{10})+ f(\frac{12}{10})+...f(\frac{20}{10}))$.

  Wenn wir für $f(x)=x^2$ einsetzen, dann erhalten wir: $O_{10}=\frac{1}{10}\cdot ((\frac{11}{10})^2+ (\frac{12}{10})^2+...(\frac{20}{10})^2)$.

  Wenn wir nun $(\frac{1}{10})^2$ ausklammern, dann erhalten wir: $O_{10}=\left( \frac{1}{10}\right)^3\cdot (11^2+12^2+...+20^2)$.

  Mit den gleichen Überlegungen erhalten wir für die Untersumme schließlich: $U_{10}=\left( \frac{1}{10}\right)^3\cdot (10^2+11^2+...+19^2)$.

  Ausgerechnet ergibt das: $2,185~FE < A < 2,485~FE$.

• Prüfe, welche Aussagen zur Streifenmethode des Archimedes stimmen.

  Tipps

  Alle Streifen haben die Breite $\frac {1}{n}$.

  Die Fläche, die von der Funktion oben begrenzt wird, kann nur näherungsweise bestimmt werden.

  Das Intervall ist immer festgelegt.

  Die Näherung wird immer genauer, je mehr Streifen verwendet werden.

  Lösung

  Archimedes von Syrakus hat sich unter anderem damit beschäftigt, wie man den Flächeninhalt bestimmen kann, der von einer Parabel, der $x$-Achse und den Intervallgrenzen eines bestimmten Intervalls eingeschlossen wird.

  Bei der so genannten Streifenmethode wählt man für die Bestimmung des Flächeninhalts in einem zuvor festgelegten Intervall eine beliebige Anzahl Streifen ($n$).

  Jeder Streifen ist gleich breit: exakt $\frac{1}{n}$.

  Nun kann man die Fläche über die Obersumme und die Untersumme annähern. Über den Flächeninhalt der gesuchten Fläche kann man nur sagen, dass er irgendwo zwischen der Obersumme und der Untersumme liegt.

  Doch je mehr Streifen man verwendet, die dann automatisch schmaler werden, desto genauer kann man den gesuchten Flächeninhalt annähern.

• Gib die passende Formel zur Berechnung der Ober- oder Untersumme für die jeweilige Aufgabenstellung an.

  Tipps

  Es gilt $\frac{2}{10}=\frac{1}{5}$.

  Die Breite der Streifen beträgt immer: Intervallbreite geteilt durch die Streifenanzahl. Den Bruch kannst du gegebenenfalls noch kürzen.

  Die Summanden sind immer davon abhängig, ob du bei der Streifenbreite den Bruch gekürzt hast oder nicht.

  An der Summandenanzahl erkennst du die Streifenanzahl.

  Lösung

  Um diese Aufgabe zu lösen, gehst du am besten so vor:

  Bestimme die Streifenbreite, indem du Intervallbreite geteilt durch Streifenanzahl rechnest. Den Bruch kannst du gegebenenfalls noch kürzen. Ist das Intervall zum Beispiel $[2;4]$, dann ist die Breite des Intervalls $2$. Sollst du $20$ Streifen verwenden, so hat jeder Streifen eine Breite von $\frac{2}{20}$ oder auch gekürzt $\frac{1}{10}$.

  Rechnest du mit dem gekürzten Bruch weiter, so lautet die Obersumme:

  $O=\frac{1}{10} \cdot (f(2+\frac{1}{10})+f(2+\frac{2}{10})+...+f(2+\frac{20}{10})$.

  Du kannst die gemischten Zahlen aber auch als Bruch schreiben:

  $O=\frac{1}{10} \cdot (f(\frac{21}{10})+f(\frac{22}{10})+...+f(\frac{40}{10}))$.

  Wenn du die Funktionsgleichung für $f(x)$ einsetzt, kannst du dann Teile ausklammern. Nehmen wir an, die Gleichung der Funktion lautet: $f(x)=\frac{1}{4} \cdot x^3$, dann setzt du ein:

  $O=\frac{1}{10} \cdot (\frac{1}{4} \cdot (\frac{21}{10})^3+\frac{1}{4} \cdot (\frac{22}{10})^3+...+\frac{1}{4} \cdot (\frac{40}{10})^3)$.

  Dann kannst du aus jedem Summanden $\frac{1}{4}$ und $(\frac{1}{10})^3$ ausklammern und erhältst:

  $O=(\frac{1}{10})^4 \cdot \frac{1}{4} \cdot (21^3+22^3+...+40^3)$.

  Für die Untersummen gehst du genau so vor.

  Wenn du im gleichen Beispiel die Streifenbreite nicht gekürzt hast, dann lautet die Obersumme:

  $O=\frac{2}{20} \cdot (f(2+\frac{2}{20})+f(2+\frac{4}{20})+...+f(2+\frac{40}{20})$.

  Du kannst die gemischten Zahlen aber auch als Bruch schreiben:

  $O=\frac{2}{20} \cdot (f(\frac{42}{20})+f(\frac{44}{20})+...+f(\frac{80}{20})$.

  Wenn du die Funktionsgleichung für $f(x)$ einsetzt, kannst du dann Teile ausklammern. Nehmen wir an, die Gleichung der Funktion lautet: $f(x)=\frac{1}{4} \cdot x^3$, dann setzt du ein:

  $O=\frac{2}{20} \cdot (\frac{1}{4} \cdot (\frac{42}{20})^3+\frac{1}{4} \cdot (\frac{44}{20})^3+...+\frac{1}{4} \cdot (\frac{80}{20})^3)$.

  Dann kannst du aus jedem Summanden $\frac{1}{4}$ und $(\frac{2}{20})^3$ ausklammern und erhältst:

  $O=(\frac{2}{20})^4 \cdot \frac{1}{4} \cdot (21^3+22^3+...+40^3)$.

  Nach diesem Prinzip kannst du in allen Intervallen mit allen Streifenanzahlen für alle (einfachen) Funktionen den Flächeninhalt mit Hilfe der Ober- und Untersumme recht schnell bestimmen.