Schrägbilder und Projektionen von Körpern

Inhaltsverzeichnis zum Thema

• Aus 3D wird 2D
• Schrägbilder konstruieren.
• Verzerrungswinkel und Verkürzungsfaktoren
• Schrägbild eines Quaders konstruieren
  • Schrägbild einer geraden Pyramide
  • Zusammengesetzte Schrägbilder
• Projektionen
• Zentralprojektionen
• Parallelprojektionen
• Zweitafelprojektionen / Dreitafelprojektionen

Aus 3D wird 2D

In der Geometrie kannst du Punkte, Strecken oder Flächen leicht auf ein Papier zeichnen. Nur wie kannst du ein dreidimensionales Objekt in dein Heft fesseln? Das kann nötig werden, wenn du dir ein genaues Bild deines Objektes machen willst. Zum Beispiel wenn du dir die Höhen, Seitenlängen und Winkel des geometrischen Körpers nicht mehr räumlich im Kopf vorstellen kannst.

Das scheinbar Unmögliche vollbringst du mit der Kamera deines Smartphones, wenn du ein Foto machst. Aus der räumlichen Welt wird ein flaches Abbild. Doch nun ist es an dir, diesen Job zu übernehmen. Keine Angst, deshalb musst du nicht gleich ein neuer Picasso werden. Denn du zeichnest nicht drauf los, sondern konstruierst nach einer klaren Anweisung.

Schrägbilder konstruieren.

Das zweidimensionale Abbild eines dreidimensionalen Körpers wird in der Geometrie Schrägbild genannt. Es zeigt den Körper aus einer bestimmten Perspektive durch den Verzerrfaktor $k$ mit dem dazugehörenden Verzerrwinkel $\alpha$. Diese beeinflussen, wie die räumliche Tiefe $t$ des dreidimensionalen Körpers abgebildet wird. Im Schrägbild wird diese dann mit einer bestimmten Länge $s$ schräg nach rechts oben gezeichnet. Es gilt:

$ k=\frac{\alpha}{90^\circ} $

$ s=k\cdot t $

In der Mathematik wird in der Regel $k=0,5$ bzw. $\alpha = 45^\circ$ gewählt.

Verzerrungswinkel und Verkürzungsfaktoren

Meistens zeichnet man Schrägbilder mit einem Winkel von $\alpha = 45^\circ$. Der zugehörige Verkürzungsfaktor $k$ für die Kanten beträgt dann $k = \frac{ 1 }{ 2 }$. Andere typische Werte sind:

• $\alpha = 30^\circ,~ k = \frac{ 2 }{ 3 }$
• $\alpha = 60^\circ,~ k = \frac{ 1 }{ 3 }$

Die folgende Abbildung zeigt drei Schrägbilder eines Würfels mit unterschiedlichen Verzerrungswinkeln.

Beträgt die Kantenlänge des Würfels beispielsweise $a = 6\ \text{cm}$, dann haben die schräg nach hinten laufenden Kanten die folgenden Längen:

• linkes Bild: $\frac{ 1 }{ 2 } \cdot 6\ \text{cm} = 3\ \text{cm}$
• mittleres Bild: $\frac{ 2 }{ 3 } \cdot 6\ \text{cm} = 4\ \text{cm}$
• rechtes Bild: $\frac{ 1 }{ 3 } \cdot 6\ \text{cm} = 2\ \text{cm}$

Schrägbild eines Quaders konstruieren

Im Folgenden wird gezeigt, wie du das Schrägbild eines Quader) konstruierst. Tipp: Zur leichteren Darstellung kannst du das Schrägbild auf kariertem Papier zeichnen.

Gesucht ist das Schrägbild eines Quaders mit den Seitenlängen $a = 4\ \text{cm}$, $b = 1\ \text{cm}$ und $c = 2\ \text{cm}$ sowie dem Verzerrungswinkel $\alpha = 45^\circ$ und dem Verkürzungsfaktor $k = \frac{ 1 }{ 2 }$.

1. Zeichne die Vorderfläche (Ansicht) des Körpers in unveränderter Größe mit $a = 4\ \text{cm}$ und $b = 1\ \text{cm}$.
2. Trage an der rechten unteren Ecke einen Winkel mit $45^\circ$ ab (oder zeichne eine Diagonale durch die quadratischen Karo-Kästchen) und zeichne die Länge $c = 2\ \text{cm}$ um den Faktor $\frac{ 1 }{ 2 }$ verkürzt, also $1\ \text{cm}$ lang.
3. Von jedem Eckpunkt der Vorderansicht zeichnest du eine Parallele zur Grundkante mit der Länge $1\ \text{cm}$. Denk daran, die unsichtbare Kante gestrichelt darzustellen.
4. Verbinde die Eckpunkte der schräg nach hinten verlaufenden Kanten mit Parallelen. Achte dabei auf die unsichtbaren Kanten, die gestrichelt gezeichnet werden.

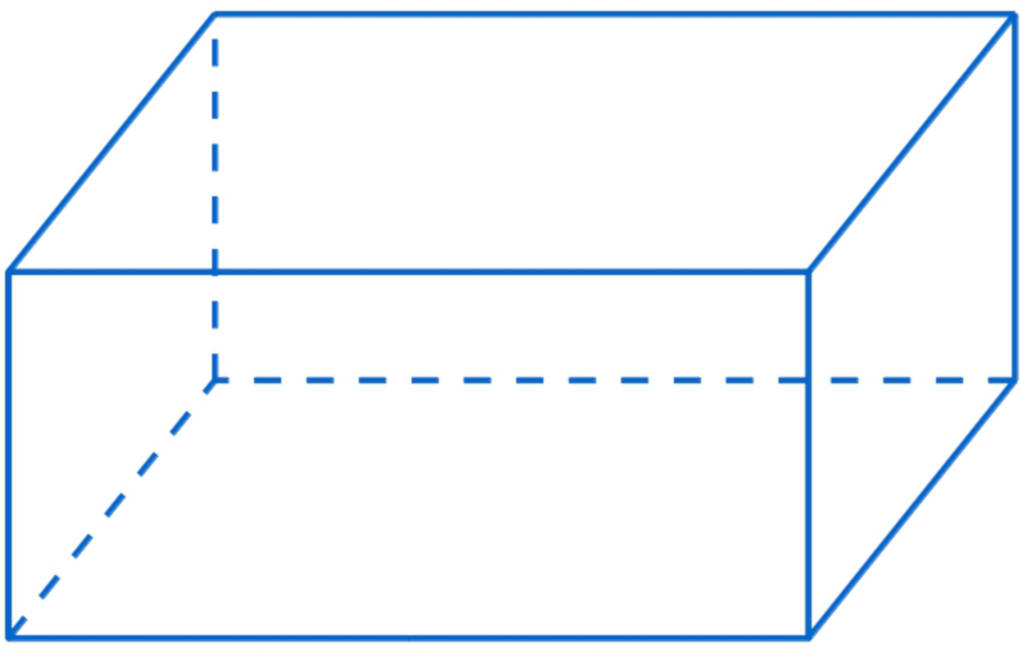
So kannst du das Schrägbild eines Quaders Zeichnen. Bei einem Würfel gehst du genauso vor.

Schrägbild einer geraden Pyramide

Das Schrägbild einer geraden Pyramide mit einer Grundfläche der Länge $l$ und Breite $b$ sowie der Höhe $h$ kannst du mit folgender Vorgehensweise zeichnen:

1. Die Länge der Grundfläche (Standfläche) wird maßstabsgetreu übertragen.
2. Diese wird nach rechts verlängert.
3. An den beiden Eckpunkten wird der Verzerrwinkel $\alpha$ angetragen. Die gezeichneten Schenkel sind parallel zueinander und zeigen nach rechts oben.
4. Die Länge der Schenkel wird mit $s=k\cdot b$ bestimmt.
5. Die Endpunkte der Schenkel werden zur Grundfläche verbunden.
6. In der Mitte der Grundfläche wird die Höhe $h$ senkrecht nach oben eingezeichnet.
7. Alle Eckpunkte der Grundfläche werden mit dem Endpunkt der Höhe verbunden.
8. Hilfslinien werden gelöscht und innen liegende Kanten gestrichelt gezeichnet.

Zusammengesetzte Schrägbilder

Möchtest du ein Schrägbild eines komplexeren geometrischen Körpers zeichnen, dann hilft es oft ihn zu zerlegen. Und zwar natürlich nicht wahllos! Sondern in geometrische Körper, deren Schrägbilder du bereits zeichnen kannst. Das Abbild entsteht dann durch die Schrägbilder des zusammengesetzten Körpers. Ein Haus könntest du als Würfel mit einer Pyramide zeichnen. Oder ein Käsestück als dreiseitiges Prisma mit einem halben Zylinder.

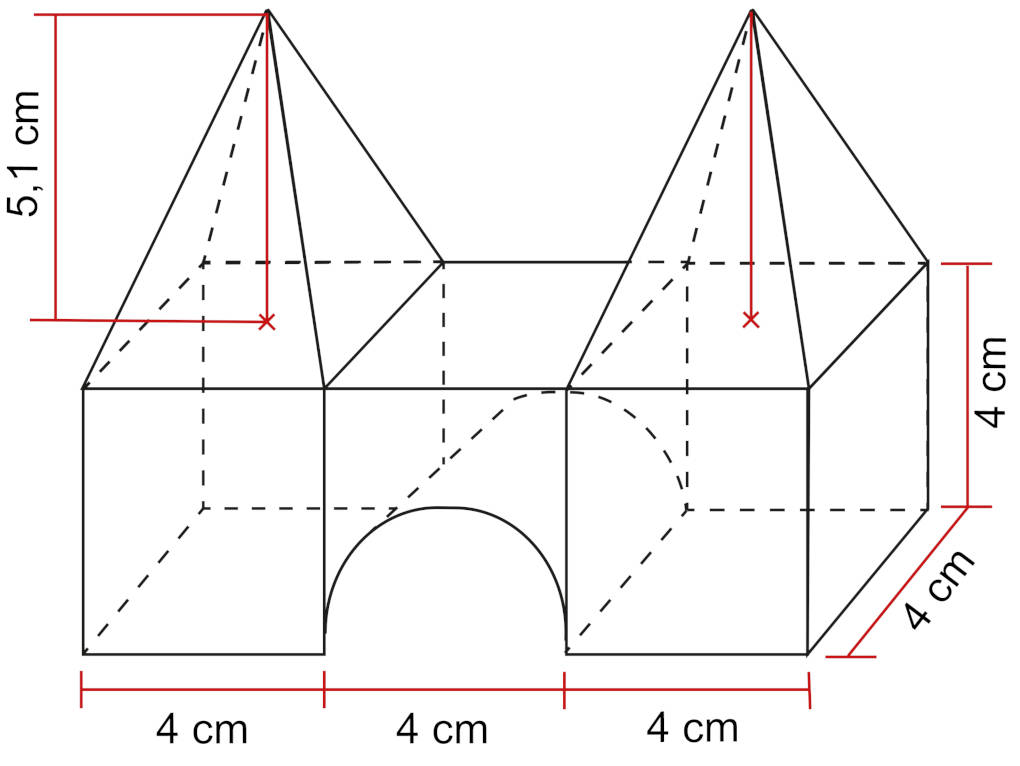
Projektionen

Das Ergebnis einer Projektion ist die Abbildung von Objekten des dreidimensionalen Raumes auf eine zweidimensionale Ebene.

Projektionen werden also verwendet, um dreidimensionale Objekte zum Beispiel auf Papier darzustellen.

• Architekten zeichnen Häuser.
• Ingenieure entwerfen Baupläne für Motoren.
• Du malst einen Baum auf ein Blatt Papier.

Es gibt verschiedene Projektionsarten

• Zentralprojektionen
• Parallelprojektionen
• Mehrtafelprojektionen: Zweitafelprojektionen / Dreitafelprojektionen

Zentralprojektionen

Bei der Zentralprojektion treffen die Projektionsgeraden sich in einem Punkt. Du kannst dir dies wie eine Lichtquelle vorstellen.

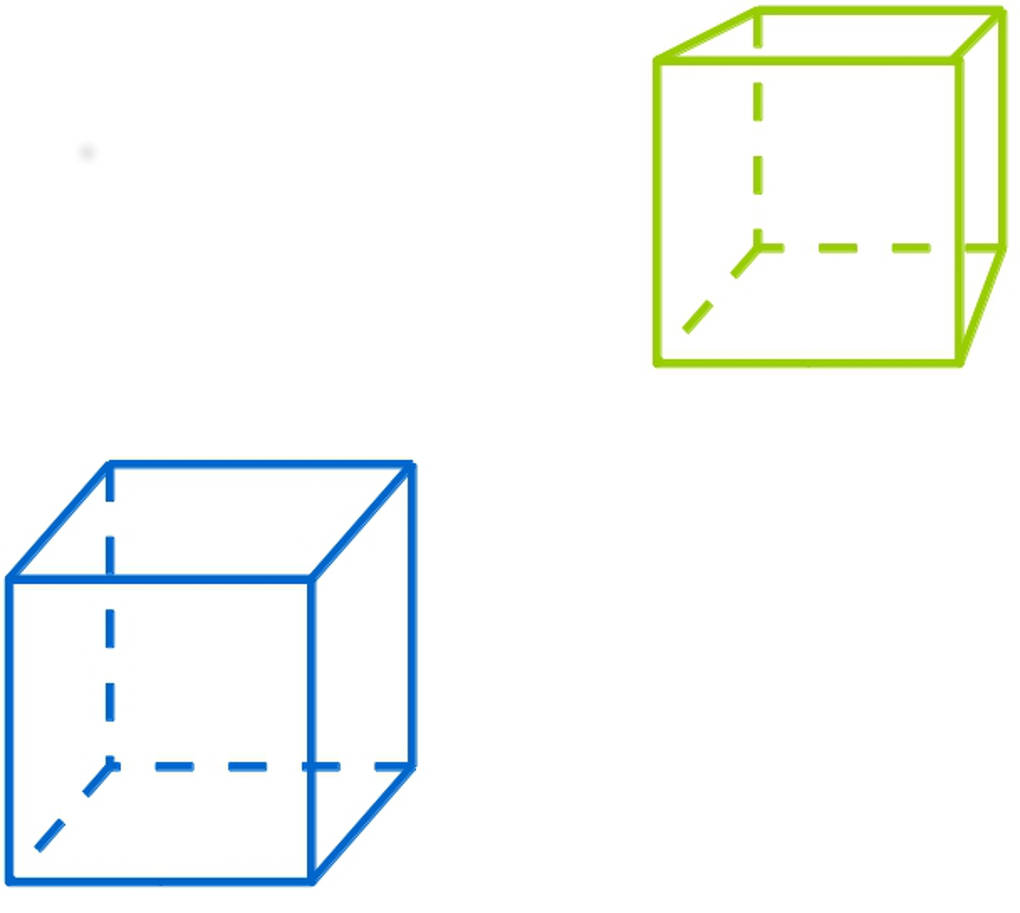
Die grüne Darstellung ist eine Zentralprojektion eines Würfels und die blaue die Parallelprojektion des gleichen Würfels. Die grüne Darstellung sieht realistischer aus. Deswegen werden Zentralprojektionen oft in der Kunst, bei Computerspielen oder in der Werbung verwendet.

Um eine Zentralprojektion anzufertigen, gehst du wie folgt vor.

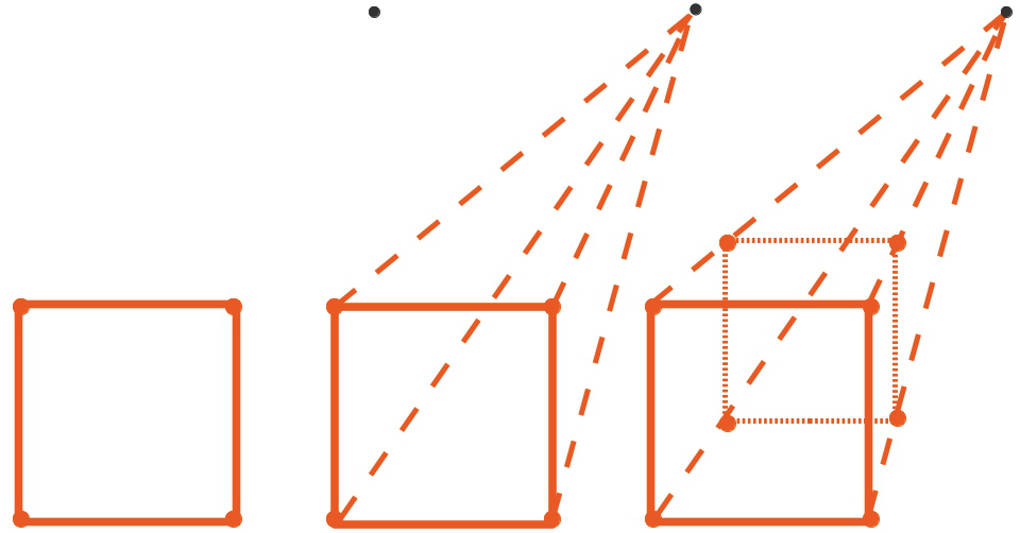
• Du zeichnest eine Seite des dreidimensionalen Objektes, zum Beispiel eines Würfels, auf ein Blatt.
• Dann verbindest du alle Eckpunkte dieser Seite mit einem Punkt.
• Nun multiplizierst du die tatsächliche Streckenlänge mit einem Verzerrfaktor und trägst die entsprechende Länge vom Punkt aus auf der zugehörigen Strecke ab.
• Die so erhaltenen Punkte werden miteinander verbunden.

Damit ergeben sich die folgenden Eigenschaften der Zentralprojektion:

• Kanten (Geraden) werden auf Kanten (Geraden) abgebildet.
• Zur Bildebene parallele Quadrate werden auf Quadrate abgebildet. Diese sind allerdings unterschiedlich groß. Allgemein bedeutet dies, dass zur Bildebene parallele Figuren auf ähnliche Figuren abgebildet werden.
• Parallele Kanten, die parallel zur Bildebene verlaufen, werden auf parallele Kanten abgebildet.
• Die senkrecht zur Bildebene verlaufenden parallelen Kanten treffen sich in einem Punkt.

Parallelprojektionen

Bei einer Parallelprojektion verlaufen die Projektionsgeraden parallel zueinander. Eine Form einer Parallelprojektion, die du sicher kennst, ist das Schrägbild.

Hier siehst du ein Schrägbild eines Quaders:

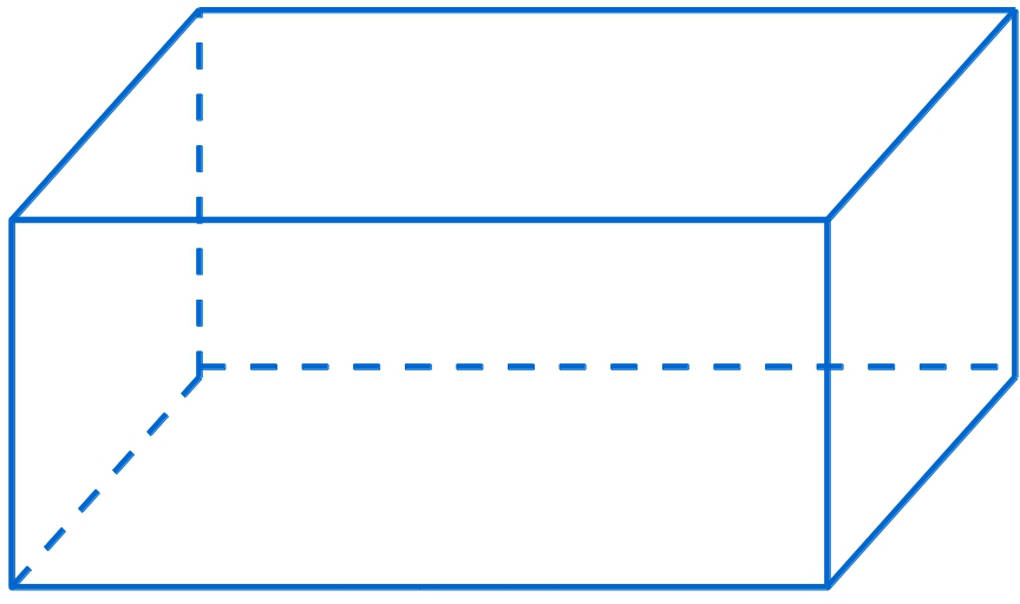
Eine Parallelprojektion hat die folgenden Eigenschaften:

• Strecken werden auf Strecken und Geraden auf Geraden abgebildet.
• Parallele Geraden werden auf parallele Geraden abgebildet.
• Zur Bildebene parallele Figuren werden auf kongruente (deckungsgleiche) Figuren abgebildet.

Zweitafelprojektionen / Dreitafelprojektionen

Ein Beispiel für die Parallelprojektion ist die Zweitafelprojektion. Hierbei wird das räumliche Objekt auf zwei Ebenen dargestellt.

Hier siehst du als Beispiel die Zweitafelprojektion eines Zylinders:

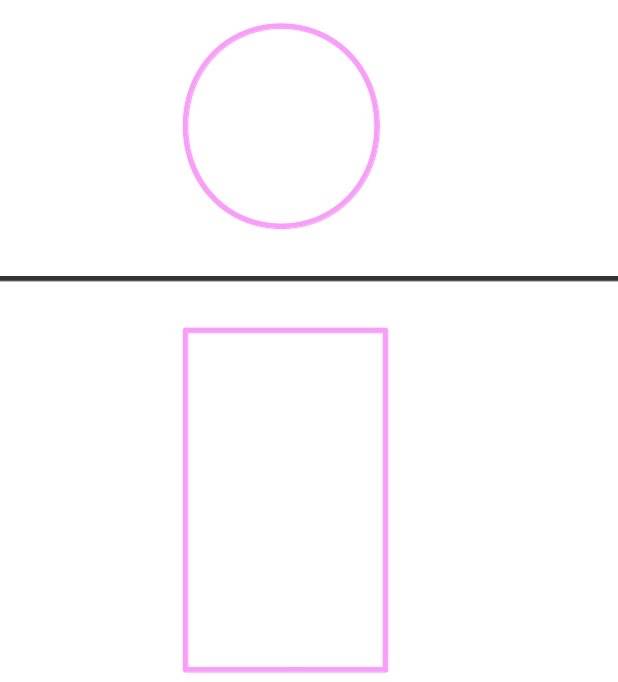
• Die schwarze Linie ist die Risskante.
• Der Kreis ist der Grundriss, die eine Ebene, die Grundfläche bei einem stehenden Zylinder.
• Das Rechteck ist der Aufriss, die zweite Ebene: Den Aufriss siehst du, wenn du von vorne auf den Zylinder schaust.

Es gibt auch Dreitafelprojektionen. Diese sind die Projektion eines räumlichen Objektes auf drei Ebenen.

• Der Grundriss: Dieser zeigt das Objekt so, als ob du direkt von oben auf das Objekt schauen würdest.
• Der Aufriss: Du erhältst einen Aufriss, wenn du das Objekt genau von vorne anschaust.
• Der Seitenriss: Dieses Mal schaust du dir das Objekt von der Seite an.

Bei einem Würfel sehen alle diese Projektionen gleich aus.