Geometrische Figuren mit Vektoren bestimmen
Du kennst bereits Dreiecke und Vierecke. Hier lernst du, wie du mithilfe von Vektoren entscheiden kannst, ob ein spezielles Viereck vorliegt.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Einführung Vektoren
- Teilverhältnisse mit Vektoren berechnen
- Besondere Dreiecke mit Vektoren bestimmen
- Rechtwinklige Dreiecke
- Gleichschenklige und gleichseitige Dreiecke
Einführung Vektoren
Vektoren beschreiben Bewegungen oder Verschiebungen im Raum. So kannst du zum Beispiel einen Punkt $A$ zu einem Punkt $B$ verschieben.
Im Folgenden lernst du verschiedene Anwendungen von Vektoren in Vektorräumen kennen.
Teilverhältnisse mit Vektoren berechnen
Du sollst prüfen, in welchem Verhältnis ein Punkt einer Strecke diese teilt. Betrachte hierfür das folgende Beispiel: Gegeben sind die Punkte $A(3|1|1)$ sowie $B(7|5|9)$. Der Punkt $T(4|2|3)$ liegt auf der Strecke $\overline{AB}$.
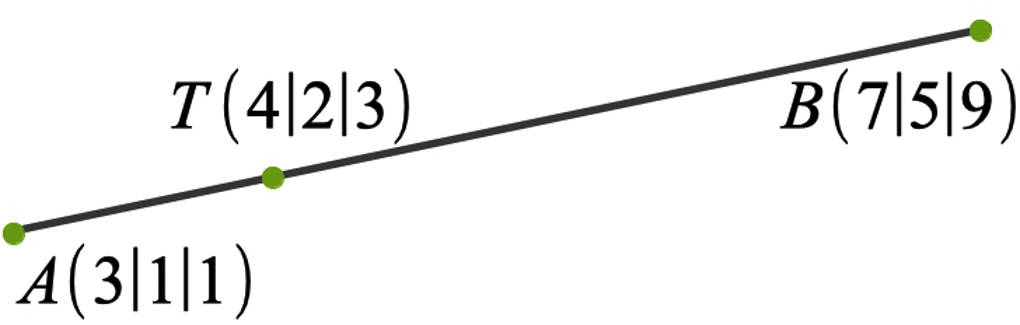
Bestimme zunächst die Verbindungsvektoren $\vec{AT}$ sowie $\vec{TB}$:
$\vec{AT}=\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$
$\vec{TB}=\begin{pmatrix} 3 \\ 3 \\ 6 \end{pmatrix}$
Du siehst, es gilt $\vec{TB}=3\cdot \vec{AT}$. Das bedeutet, dass die Vektoren kollinear sind. Insbesondere ist damit auch nachgewiesen, dass der Punkt $T$ auf der Strecke $\overline{AB}$ liegt.
Da der Vektor $\vec{TB}$ das Dreifache des Vektors $\vec{AT}$ ist, kannst du daraus schließen, dass der Punkt $T$ die Strecke $\overline{AB}$ im Verhältnis $1:3$ teilt.
Ebenso gehst du vor, wenn du Teilverhältnisse in Körpern, zum Beispiel Quadern, bestimmen möchtest.
Besondere Dreiecke mit Vektoren bestimmen
Neben Teilverhältnissen kannst du mithilfe von Vektoren auch entscheiden, ob ein besonderes Dreieck vorliegt.
Wenn du drei Punkte gegeben hast und untersuchen sollst, ob diese ein Dreieck bilden, schreibst du die Verbindungsvektoren von jeweils zwei der drei Vektoren auf. Sind diese nicht kollinear, so liegt ein Dreieck vor. Andernfalls liegen die drei Punkte auf einer Geraden.
Rechtwinklige Dreiecke
Betrachte die drei Punkte $A(-1|2|2)$, $B(3|1|1)$ und $C(0|4|4)$. Weise nach, dass das Dreieck $\triangle{ABC}$ rechtwinklig ist mit dem rechten Winkel in $A$. Da der Scheitelpunkt $A$ des rechten Winkels gegeben ist, untersuchst du die folgenden Verbindungsvektoren:
$\vec{AB}=\begin{pmatrix} 4 \\ -1 \\ -1 \end{pmatrix}$
$\vec{AC}=\begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}$
Diese beiden Vektoren sind nicht kollinear. Berechne nun das Skalarprodukt der beiden Vektoren. Ist dieses $0$, so sind die Vektoren orthogonal zueinander.
$\vec{AB}\star \vec{AC}=\begin{pmatrix} 4 \\ -1 \\ -1 \end{pmatrix}\star\begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}=4-2-2=0$
Das vorliegende Dreieck ist also rechtwinklig.
Gleichschenklige und gleichseitige Dreiecke
Bei gleichschenkligen Dreiecken sind mindestens zwei Seiten gleich lang. Die Seitenlängen eines Dreiecks, welches durch drei Punkte im $\mathbb{R}^{3}$ gegeben ist, kannst du als Längen der Verbindungsvektoren berechnen. Betrachte das Dreieck, welches durch die Punkte $A(2|1|1)$, $B(6|1|1)$ und $C(4|3|2)$ beschrieben ist.
Du berechnest die Länge der Verbindungsvektoren:
$|\vec{AB}|=\left|\begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\right|=4$
$|\vec{AC}|=\left|\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}\right|=3$
$|\vec{BC}|=\left|\begin{pmatrix} -2 \\ 2\\ 1 \end{pmatrix}\right|=3$
Es gilt $\overline{AC}=\overline{BC}$. Damit ist das Dreieck $\triangle{ABC}$ gleichschenklig.
Ebenso weist du nach, ob ein Dreieck gleichseitig ist, also alle drei Seiten gleich lang sind.
Besondere Vierecke mit Vektoren bestimmen
So ähnlich wie bei dem Nachweis von besonderen Dreiecken gehst du vor, wenn du besondere Vierecke nachweisen möchtest.
Dies schauen wir uns einmal am Beispiel von Quadraten an: Die Punkte $A(2|1|1)$, $B(6|1|1)$ sowie $C(6|1|5)$ sollen durch einen weiteren Punkt $D$ zu einem Quadrat ergänzt werden.
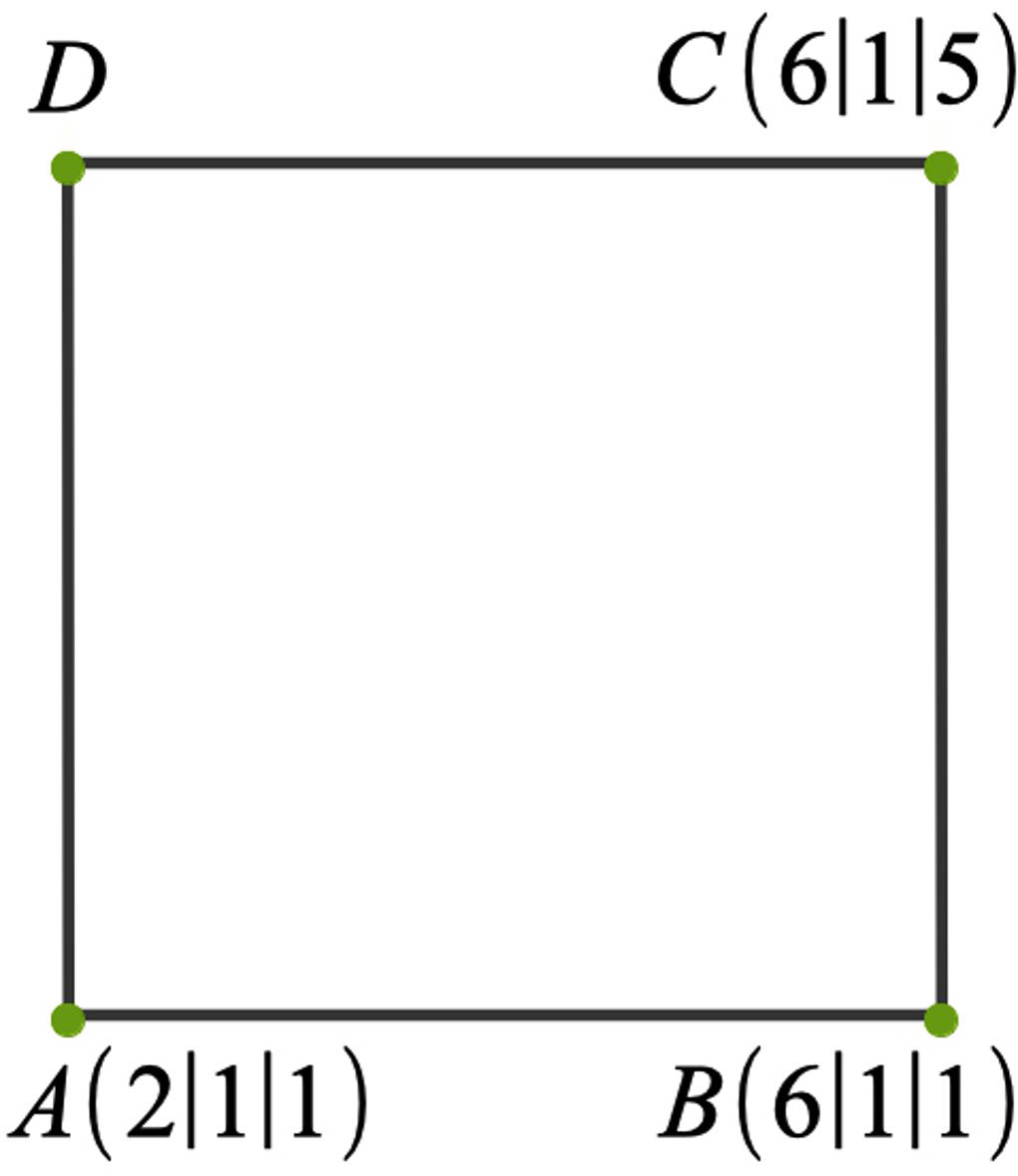
Da $|\vec{AB}|=|\vec{BC}|=4$ sowie $\vec{AB}\perp\vec{BC}$ ist, kannst du den Punkt $D$ so bestimmen:
$\vec d=\vec c+\vec{BA}=\begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix}+ \begin{pmatrix} -4 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix}$
Du hast den Punkt $D(2|1|5)$ gefunden. Das Viereck $ABCD$ ist ein Quadrat.
Alle Videos zum Thema
Videos zum Thema
Geometrische Figuren mit Vektoren bestimmen (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Geometrische Figuren mit Vektoren bestimmen (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung






 Teilverhältnisse in geometrischen Figuren bestimmen – Beispiel (1)
Teilverhältnisse in geometrischen Figuren bestimmen – Beispiel (1)
 Teilverhältnisse in geometrischen Figuren bestimmen – Beispiel (2)
Teilverhältnisse in geometrischen Figuren bestimmen – Beispiel (2)
 Besondere Dreiecke mit Vektoren bestimmen
Besondere Dreiecke mit Vektoren bestimmen
 Besondere Vierecke mit Vektoren bestimmen
Besondere Vierecke mit Vektoren bestimmen









