Polynomdivision
Die Polynomdivision ähnelt stark der schriftlichen Division und beruht auf der Linearfaktor-Zerlegung.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Lösen quadratischer Gleichungen und Funktionen
- Lösen von Gleichungen und Funktionen höheren Grades
- Durchführung der Polynomdivision: 1. Schritt
- Durchführung der Polynomdivision: 2. Schritt
- Durchführung der Polynomdivision: 3. Schritt
- Alternative zur Polynomdivision
Lösen quadratischer Gleichungen und Funktionen
Um Funktionen oder Gleichung zweiten Grades, also quadratische Funktionen beziehungsweise quadratische Gleichungen, zu lösen, beziehungsweise die Nullstellen von solchen Funktionen zu berechnen, kannst du zum Beispiel folgende Möglichkeiten nutzen:
Ist zum Beispiel die quadratische Funktion
$f(x) = x^{2}-2x-8$
gegeben, so kannst du die Nullstellen mit Hilfe der pq-Formel ermitteln. Diese lauten:
- $x_{1}=-2$
- $x_{2}=4$
Ein anderer Weg eine quadratische Gleichung zu lösen oder die Nullstellen einer quadratische Funktion zu berechnen ist die Linearfaktorzerlegung. Die Linearfaktorzerlegung der quadratischen Funktion $f(x) = x^{2}-2x-8$ lautet:
$f(x) = x^{2}-2x-8 = (x+2) \cdot (x-4)$.
Die Funktion nimmt den Funktionswert $0$, sobald einer der Faktoren $0$ ist. Der erste Faktor, also $(x+2)$, ist genau dann null, wenn du für $x$ den Wert $2$ einsetzt. Der Faktor $(x-4)$ ist genau dann $0$, wenn du den Wert $4$ für $x$ einsetzt.
Lösen von Gleichungen und Funktionen höheren Grades
Bei Gleichungen und Funktionen höheren Grades kannst du die sogenannte Polynomdivision nutzen, um anschließend eines der oben genannten Lösungsverfahren anwenden zu können. Die Polynomdivision nutzt als Grundlage die Linearfaktorzerlegung, aber genau umgedreht. Ziel ist es, dass du zunächst einen dieser Linearfaktoren findest und die Ausgangsgleichung durch diesen Linearfaktor teilst. Übrig bleibt eine eine Gleichung, deren Grad um $1$ kleiner ist. Aus einer kubischen Funktion (Funktion dritten Grades) wird somit eine quadratische Funktion und so weiter.
Durchführung der Polynomdivision: 1. Schritt
An einem Beispiel lässt sich das Verfahren am besten verstehen. Willst du also beispielsweise die Nullstellen der kubischen Funktion
$f(x)=x^{3}-2x^{2}-5x+6$
finden, so musst du zunächst eine Nullstelle der Funktion ermitteln. Diese erste Nullstelle kannst du durch raten oder durch das Zeichnen der Funktion finden.
Um die Nullstelle zu raten, ermittelst du die Teiler des Terms ohne Faktor $x$, also hier im Beispiel die Teiler der $6$, und setzt diesen Wert in die Funktionsgleichung für $x$ ein. Ist das Ergebnis $0$, so hast du die erste Nullstelle gefunden. Mögliche Teiler sind $1$, $-1$, $2$, $-2$, $3$, $-3$, $6$ oder $-6$.
Setzt du zum Beispiel für $x$ die $1$ in die Funktionsgleichung ein erhältst du:
$f(1)=1^{3} -2 \cdot 1^{2} - 5 \cdot 1 +6 = 1 -2-5+6=0$.
Das bedeutet, dass mit $x_{1}=1$ die erste Nullstelle der Funktion gefunden ist.
Der erste Linearfaktor der Funktion $f(x)=x^{3}-2x^{2}-5x+6$ ist also $(x-1)$. Die Linearfaktorzerlegung der Funktion lautet nun:
$f(x)=x^{3}-2x^{2}-5x+6 = (x-1) \cdot y \cdot z$.
$y$ und $z$ stellen dabei die noch unbekannten Linearfaktoren dar. Setzt du in den ersten Linearfaktor die $1$, also den Wert der ersten Nullstelle ein, ist dieser Faktor $0$. Egal, was die anderen Linearfaktoren ergeben, ist der Funktionswert dann auch $0$, da hier mit $0$ multipliziert wird.
Durchführung der Polynomdivision: 2. Schritt
Teilst du nun den Funktionsterm durch den bereits gefundenen Linearfaktor, so bleiben auf der rechten Seite nur noch die beiden bisher noch nicht gefundenen Linearfaktoren übrig:
$\begin{array}{rlcll} x^{3}-2x^{2}-5x+6 &~&=& (x-1) \cdot y \cdot z & \vert \div (x-1) \\ (x^{3}-2x^{2}-5x+6) &\div (x-1) &=& y \cdot z & ~ \end{array}$
Die Divisionsaufgabe auf der linken Seite wird als Polynomdivision bezeichnet:
$(x^{3}-2x^{2}-5x+6) \div ~(x-1)$
Teile den ersten Term des Dividenden $\color{#669900}{x^{3}}-2x^{2}-5x+6$ durch den ersten Term des Divisors $\color{#669900}{x}-1$. Das Ergebnis schreibst du hinter das Gleichheitszeichen:
$x^{3} \div x =x^{2}$
$(x^{3}-2x^{2}-5x+6) \div (x-1) = x^{2}$
Nun multiplizierst du den Divisor $(x-1)$ mit dem Zwischenergebnis $x^{2}$, also: $(x-1) \cdot x^{2} = \color{#669900}{x^{3}-x^{2}}$. Dieses Ergebnis schreibst du stellengerecht unter das erste Polynom:
$\begin{array}{l} (x^{ 3 }-2x^{ 2 } -5x +6 ) \div (x-1)=x^{ 2 } \\ (\color{#669900}{x^{ 3 }-x^{ 2 }}) \end{array}$
Subtrahiere jetzt $x^{3}-x^{2}$ vom ersten Polynom:
$\begin{array}{l} ~~~( x^{ 3 } -2x^{ 2 } -5x +6 ) \div (x-1)=x^{ 2 } \\ \color{#669900}{-}\underline{( x^{ 3 } -x^{ 2 })} \end{array}$
Schreibe das Ergebnis unter den Strich:
$\begin{array}{l} ~~~( x^{ 3 } -2x^{ 2 } -5x +6 ) \div (x-1)=x^{ 2 } \\ -\underline{( x^{ 3 } -x^{ 2 })} \\ ~~~~~~~~~-x^{2}\end{array}$
Du merkst, dass der erste Term $x^{3}$ dabei wegfällt.
Bringe die restlichen Terme des ersten Polynoms nach unten:
$\begin{array}{l} ~~~( x^{ 3 } -2x^{ 2 } -5x +6 ) \div (x-1)=x^{ 2 } \\ -\underline{( x^{ 3 } -x^{ 2 })} \\ ~~~~~~~~~-x^{2}\color{#669900}{-5x+6} \end{array}$
Nun beginnt die Division von vorn. Teile jetzt den ersten Term des Restterms $-x^{2}-5x+6$, also $-x^{2}$ durch den ersten Term des Divisors, also wieder $x$:
$\begin{array}{l} ~~~( x^{ 3 } -2x^{ 2 } -5x +6 ) \div (\color{#669900}{x}-1)=x^{ 2 }\color{#669900}{-x} \\ -\underline{( x^{ 3 } -x^{ 2 })} \\ ~~~~~~~~~\color{#669900}{-x^{2}}-5x+6 \end{array}$
und wiederhole die Schritte, bis am Ende $0$ bei der Subtraktion herauskommt.
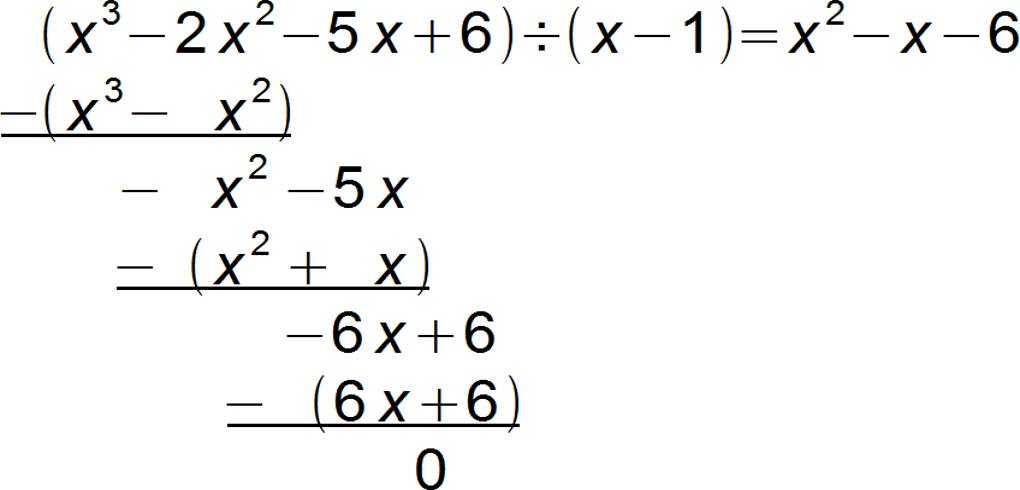
Durchführung der Polynomdivision: 3. Schritt
Nun musst du nur noch die Lösungen des Polynoms $0=x^{2}-x+6$ bestimmen. Da es sich hierbei um eine quadratische Gleichung handelt, kannst du nun zum Beispiel wieder die pq-Formel verwenden.
Die Lösungen dieses Polynoms sind $x_2=-2$ und $x_3=3$.
Damit hast du nun alle Nullstellen der kubischen Funktion $f(x)=x^{3}-2x^{2}-5x+6$ gefunden. Die Nullstellen sind $x_1=1$, $x_2=-2$ und $x_3=3$.
In Linearfaktorzerlegung lautet die Funktion also:
$f(x)=x^{3}-2x^{2}-5x+6=(x-1) \cdot (x+2) \cdot (x-3)$.
Alternative zur Polynomdivision
Um die Lösungen für Gleichungen oder die Nullstellen für Funktionen höheren Grades zu berechnen, kannst du alternativ das sogenannte Horner-Schema nutzen. Wie bei der Polynomdivision muss du hierfür zunächst eine Nullstelle oder Lösung raten. Anschließend kannst du mit Hilfe des Algorithmus des Horner-Schemas, wie im verlinkten Video beschrieben, die übrigen Lösungen beziehungsweise die übrigen Nullstellen finden.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Polynomdivision (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Polynomdivision (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung






 Polynomdivision – Erklärung
Polynomdivision – Erklärung
 Addition von Polynomen
Addition von Polynomen









