Lösungswege für quadratische Gleichungen
Entdecke die Lösungswege von quadratischen Gleichungen in allgemeiner und Normalform mit der pq-Formel. Erfahre, wie die Anzahl der Lösungen berechnet wird und wie man mit der Linearfaktorzerlegung einfach Lösungen ablesen kann. Interessiert? Dies und vieles mehr findest du im folgenden Text!
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Grundlagen zum Thema Lösungswege für quadratische Gleichungen
Quadratische Gleichungen lösen – Mathematik
Lina ist Sachbearbeiterin in der Abteilung für Gleichungen. Eigentlich bearbeitet sie nur lineare Gleichungen, aber heute liegt diese Gleichung auf ihrem Tisch:
$3\,x^{2} + 9\,x + 6 = 0$
So etwas bearbeitet sie normalerweise nicht. Es handelt sich um eine quadratische Gleichung. Wie löst man quadratische Gleichungen? Um das herauszufinden, muss sie sich mit den Lösungswegen für quadratische Gleichungen beschäftigen.
In diesem Text werden die Lösungswege für beliebige quadratische Gleichungen vorgestellt, die in allgemeiner Form, in Normalform oder in Linearfaktorzerlegung/Produktform gegeben sind. Der Fokus liegt darauf, wie man quadratische Gleichungen rechnerisch lösen kann.
Quadratische Gleichungen lösen – Erklärung
Jede quadratische Gleichung ist in allgemeiner Form
$a\,x^{2} + b\,x + c = 0$
und in Normalform
$x^{2} + p\,x + q = 0$
darstellbar. Die jeweiligen Gleichungen unterscheiden sich durch die Koeffizienten ihrer Glieder. Jede quadratische Gleichung in allgemeiner Form kann man in eine Gleichung in Normalform überführen. Die Lösungsmenge der Gleichung ändert sich dabei nicht. Die Koeffizienten führen auf die Lösungen dieser Gleichungen. Die Koeffizienten nennen wir $a$, $b$ und $c$ in der allgemeinen Form sowie $p$ und $q$ in der Normalform.
Die Lösungen einer quadratischen Gleichung in allgemeiner Form können wir mithilfe der Mitternachtsformel bestimmen. Ist die Gleichung in Normalform gegeben, benutzen wir die
In diesem Text beschränken wir uns auf die Anwendung der pq-Formel. Diese lautet:
$x_{1,2} = - \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4}-q}$
Die Formel gibt die beiden Lösungen einer quadratischen Gleichung in Normalform an.
Schauen wir uns dafür ein Beispiel an. Die folgende quadratische Gleichung ist in allgemeiner Form gegeben.
$3\,x^{2} + 9\,x + 6 = 0$
Indem wir sie durch den Koeffizienten des quadratischen Glieds – also durch $3$ – teilen, bringen wir sie in Normalform.
$3\,x^{2} + 9\,x + 6 = 0 \quad |:3$
$x^{2} + 3\,x + 2 = 0$
In dieser Form können wir die Koeffizienten $p$ und $q$ direkt ablesen.
$p = 3 \quad q = 2$
Nun können wir die pq-Formel anwenden. Wir setzen die Koeffizienten in die Formel ein und rechnen zuerst aus, was unter der Wurzel steht.
$x_{1,2} = - \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4}-q}$
$x_{1,2} = - \frac{3}{2} \pm \sqrt{\frac{3^{2}}{4}-2}$
$x_{1,2} = - \frac{3}{2} \pm \sqrt{\frac{1}{4}}$
Wir erhalten unter der Wurzel eine positive Zahl. Die Wurzel aus $\frac{1}{4}$ ist $\frac{1}{2}$. Die Gleichung besitzt zwei Lösungen, da sich zwischen den Brüchen ein Plusminuszeichen ($\pm$) befindet. Das bedeutet, es wird einmal plus und einmal minus gerechnet. Für die erste Lösung addieren wir, für die zweite Lösung subtrahieren wir.
$\qquad \qquad x_{1,2} = - \frac{3}{2} \pm \frac{1}{2}$
$x_1 = - \frac{3}{2} + \frac{1}{2} \qquad x_2 = - \frac{3}{2} - \frac{1}{2}$
$\Rightarrow x_1 = -1 \qquad \Rightarrow x_2 = -2$
Die Lösungen für diese Gleichung lauten also $-1$ und $-2$.
Quadratische Gleichungen – Anzahl der Lösungen
Schauen wir uns ein weiteres Beispiel an. Zuerst muss die Gleichung wieder in Normalform gebracht werden.
$3\,x^{2} + 6\,x + 6 = 0 \quad |:3$
$x^{2} + 2\,x + 2 = 0$
Nun lesen wir die Koeffizienten ab.
$p=2 \quad q=2$
Wir setzen sie in die pq-Formel ein und ermitteln den Wert unter der Wurzel.
$x_{1,2} = - \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4}-q}$
$x_{1,2} = - \frac{2}{2} \pm \sqrt{\frac{2^{2}}{4}-2}$
$x_{1,2} = - 1 \pm \sqrt{-1}$
Wir erhalten eine negative Zahl unter der Wurzel. Da man aus einer negativen Zahl keine Wurzel ziehen kann, hat diese Gleichung keine Lösung. Allgemein lässt sich über die pq-Formel Folgendes sagen:
Die Anzahl der Lösungen der entsprechenden quadratischen Gleichung hängt davon ab, welche Zahl sich unter der Wurzel befindet. Steht dort eine positive Zahl, besitzt die Gleichung zwei Lösungen. Steht unter Wurzel eine Null, dann gibt es eine Lösung. Steht eine negative Zahl unter der Wurzel, dann gibt es keine Lösung.
Quadratische Gleichungen durch Ablesen lösen
Neben der allgemeinen Form und der Normalform gibt es noch eine dritte Art der Darstellung quadratischer Gleichungen. Dabei handelt es sich um die Linearfaktorzerlegung.
$a \cdot (x - m) \cdot (x - n) = 0$
Im ersten Moment sieht das nicht nach einer quadratischen Gleichung aus. Multipliziert man jedoch die beiden Klammern, so sieht man, dass ein Term mit $x^{2}$ entsteht.
$a \cdot (x^{2} - mx - nx + mn) = 0$
In der Linearfaktorzerlegung kann man den Satz vom Nullprodukt anwenden: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist. Die Faktoren sind $a$ sowie $(x - m)$ und
Schauen wir uns dazu ein Beispiel an.
$2 \cdot (x - 1) \cdot (x + 3) = 0$
Da $2 \neq 0$ ist, muss nach dem Satz vom Nullprodukt einer der beiden anderen Faktoren, also $(x-1)$ oder $(x+3)$, null sein. Um die Lösungen der quadratischen Gleichung zu ermitteln, müssen wir also die beiden Klammern null setzen.
$ x_1 - 1 = 0 \qquad \text{oder} \qquad x_2 + 3 = 0$
Die erste dieser beiden Gleichungen ist äquivalent zu $x_1 = 1$, die zweite zu $x_2 = - 3$.
Wir erhalten die Lösungen $1$ und $-3$. Das ist, bis auf die Vorzeichen, genau das, was in den Klammern stand. Man kann die Lösungen der quadratischen Gleichung also an der Linearfaktorzerlegung einfach ablesen. Weil diese Form die Lösungen aber direkt enthält, gibt es diese Form nicht für quadratische Gleichungen, die keine Lösungen enthalten.
Die Linearfaktorzerlegung existiert nicht, wenn die Gleichung keine Lösung besitzt.
Zusammenfassung – quadratische Gleichungen lösen
Die folgenden Stichpunkte fassen das Wichtigste zum Lösen von quadratischen Gleichungen mithilfe der pq-Formel noch einmal zusammen.
- Jede quadratische Gleichung kann in ihre allgemeine Form gebracht werden. Sie besitzt dann drei Koeffizienten: $ \, a\,x^{2} + b\,x + c = 0$.
- Du kannst die allgemeine Form immer in die Normalform umwandeln, indem du die ganze Gleichung durch $a$ teilst. In der Normalform ist der Koeffizient vor dem quadratischen Glied $1$. Die Koeffizienten $p$ und $q$ können dann direkt abgelesen werden: $ \, x^{2} + p\,x + q = 0$.
- Du verwendest die pq-Formel, um die Lösungen zu ermitteln: $ \, x_{1,2} = - \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4}-q}$.
- Abhängig von der Zahl unter der Wurzel gibt es zwei, eine oder keine Lösung.
- Eine quadratische Gleichung kann auch als Linearfaktorzerlegung gegeben sein:
$ \, a \cdot (x - m) \cdot (x - n) = 0$ . - Die Linearfaktorzerlegung existiert nicht, wenn die Gleichung keine Lösung besitzt.
- Die Lösungen können in der Linearfaktorzerlegung direkt abgelesen werden. Die Gleichung kann eine oder zwei Lösungen besitzen.
Hast du jetzt Lust bekommen, mehr Aufgaben zum Lösen quadratischer Gleichungen zu erledigen? Hier auf der Seite findest du Arbeitsblätter und Übungen zum Thema Lösen von quadratischen Gleichungen.
Transkript Lösungswege für quadratische Gleichungen
Lina ist Sachbearbeiterin in der Abteilung für Gleichungen. Für manche wäre so ein Job ja die Hölle. Aber sie bearbeitet seit 35 Jahren lineare Gleichungen und das macht ihr viel Spaß, weil es so, äh, abwechslungsreich ist. Aber heute hat sie eine seltsame Gleichung bekommen, so etwas bearbeitet sie doch eigentlich gar nicht! Die Gleichung ist nämlich nicht linear, sondern quadratisch. Aber wie kann sie die lösen? Dazu beschäftigt sich Lina mit den Lösungswegen für quadratische Gleichungen. In diesem Video werden die Lösungswege für beliebige quadratische Gleichungen vorgestellt, die in allgemeiner Form, Normalform oder Linearfaktorzerlegung, auch Produktform genannt, gegeben sind. Beginnen wir mit den ersten beiden Formen: Jede quadratische Gleichung ist in allgemeiner Form und in Normalform darstellbar. Die einzelnen quadratischen Gleichungen unterscheiden sich nur durch die Koeffizienten ihrer Glieder und die Koeffizienten führen daher auch auf die Lösungen dieser Gleichungen. Die Lösungen einer quadratischen Gleichung in allgemeiner Form können wir mit Hilfe der Mitternachtsformel bestimmen. Ist sie in Normalform gegeben, benutzen wir die pq-Formel. Die quadratische Ergänzung funktioniert für beide Formen. In diesem Video beschränken wir uns auf die Anwendung der pq-Formel. Schauen wir uns dazu ein Beispiel an. Diese quadratische Gleichung ist in allgemeiner Form gegeben. Indem wir sie durch den Koeffizienten des quadratischen Glieds teilen, bringen wir sie in Normalform. In dieser Form können wir die Koeffizienten p und q direkt ablesen: 'p ist gleich 3' und 'q ist gleich 2'. Dann können wir die pq-Formel anwenden. Wir setzen die Koeffizienten ein und rechnen zuerst aus, was unter der Wurzel steht. Wir erhalten eine positive Zahl. Die Wurzel aus ein Viertel ist ein Halb. Die Gleichung besitzt zwei Lösungen, weil hier einmal plus und einmal Minus gerechnet wird. Für die erste Lösung addieren wir und erhalten: x1 gleich 'Minus 1'. Für die zweite Lösung subtrahieren wir und erhalten: x2 gleich 'Minus 2'. Die Lösungen für diese Gleichung lauten also 'Minus 1' und 'Minus 2'. Schauen wir uns noch dieses Beispiel an. Wir bringen die Gleichung in Normalform und lesen die Koeffizienten ab: 'p ist gleich 2' und 'q ist gleich 2'. Wir setzen sie in die pq-Formel ein und ermitteln den Wert unter der Wurzel. Wir erhalten eine negative Zahl. Weil man aus einer negativen Zahl keine Wurzel ziehen kann, hat diese Gleichung keine Lösung. Allgemein lässt sich über die pq-Formel folgendes sagen: Die Anzahl der Lösungen der entsprechenden quadratischen Gleichung hängt davon ab, welche Zahl sich unter der Wurzel befindet. Wenn dort eine positive Zahl steht, gibt es zwei Lösungen. Wenn unter der Wurzel eine Null steht, eine Lösung und wenn unter der Wurzel eine negative Zahl steht, keine Lösung. Neben der allgemeinen Form und der Normalform gibt es noch eine dritte Darstellung quadratischer Gleichungen. Dabei handelt es sich um ihre Linearfaktorzerlegung. Im ersten Moment sieht sie nicht nach einer quadratischen Gleichung aus. Wenn man aber die beiden Klammern ausmultipliziert, sieht man, dass ein 'x Quadrat' entsteht. In der Linearfaktorzerlegung kann man den Satz vom Nullprodukt anwenden. Der besagt, dass ein Produkt immer dann Null ist, wenn einer der Faktoren Null ist. Schauen wir uns dazu ein Beispiel an. Um die Lösungen zu ermitteln, müssen wir die beiden Klammern Null setzen. Wir erhalten die Lösungen 'plus 1' und 'minus 3'. Das ist, bis auf die Vorzeichen, genau das, was in den Klammern stand. Man kann die Lösungen hier also einfach ablesen. Weil diese Form die Lösungen aber direkt enthält, gibt es diese Form nicht für quadratische Gleichungen, die keine Lösung besitzen. Fassen wir das noch einmal zusammen: Jede quadratische Gleichung kann in ihre allgemeine Form gebracht werden. Sie besitzt dann drei Koeffizienten. Du kannst sie immer in Normalform umwandeln, indem du die ganze Gleichung durch 'a' teilst. In dieser Form ist der Koeffizient vor dem quadratischen Glied 1. Wir können dann p und q direkt ablesen. Du verwendest die pq-Formel, um die Lösungen zu ermitteln. Abhängig von der Zahl unter der Wurzel, gibt es zwei, eine oder keine Lösung. Eine quadratische Gleichung kann auch als Linearfaktorzerlegung gegeben sein. Diese Form existiert aber nicht für quadratische Gleichungen, die keine Lösung besitzen. Die Lösungen kannst du direkt ablesen. Gar nicht so schlecht, diese quadratischen Gleichungen, findet Lina. Also für Lina ist das nicht die Hölle!
Lösungswege für quadratische Gleichungen Übung
-
Gib die Formen für quadratische Gleichungen an.
TippsIn einer quadratischen Gleichung ist die Variable zur zweiten Potenz erhoben.
Teilst du die allgemeine Form einer quadratischen Gleichung durch den Koeffizienten des quadratischen Gliedes, so erhältst du die Normalform und kannst die $pq$-Formel anwenden.
LösungEine quadratische Gleichung kann in unterschiedlichen Formen vorliegen. Die allgemeine Form lautet:
- $\underbrace{ax^2}_{\text{quadratisches Glied}}+\underbrace{bx}_{\text{lineares Glied}}+\underbrace{c}_{\text{absolutes Glied}}=0$
- $x^2+px+q=0$
Eine quadratische Gleichung in Normalform lösen wir mithilfe der $pq$ -Formel. Hat eine quadratische Gleichung eine oder zwei Lösungen, so kann man sie auch in der Produktform angeben. Diese nennt man auch Linearfaktorzerlegung. Sie lautet allgemein:
- $(x-m)(x-n)=0$
-
Bestimme die Lösungen der quadratischen Gleichungen.
TippsDie Normalform einer quadratischen Gleichung lautet:
- $x^2+px+q=0$
Die $pq$-Formel lautet:
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
Um die Anzahl der Lösungen einer quadratischen Gleichung in Normalform zu bestimmen, betrachtet man die Diskriminante der entsprechenden $pq$-Formel:
- $\frac {p^2}4-q>0$: zwei Lösungen
- $\frac {p^2}4-q=0$: eine Lösung
- $\frac {p^2}4-q<0$: keine Lösung
LösungWir überführen die quadratischen Gleichungen in die Normalform, indem wir die Gleichungen jeweils durch ihren Koeffizienten im quadratischen Glied teilen. So erhalten wir Gleichungen in der Normalform:
- $x^2+px+q=0$
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
- $\frac {p^2}4-q>0$: zwei Lösungen
- $\frac {p^2}4-q=0$: eine Lösung
- $\frac {p^2}4-q<0$: keine Lösung
Gleichung 1
$\begin{array}{lllll} & 3x^2+9x+6 &=& 0 & \vert :3 \\ & x^2+3x+2 &=& 0 & \\ \end{array}$
Mit den Koeffizienten $p=3$ und $q=2$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 32\pm\sqrt{\frac {3^2}4-2} \\ & x_{1,2} &=& -\frac 32\pm\sqrt{\frac 94-\frac 84} \\ & x_{1,2} &=& -\frac 32\pm\sqrt{\frac 14} \\ & x_{1,2} &=& -\frac 32\pm\frac 12 \\ \\ & x_1 &=& -1 \\ & x_2 &=& -2 \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -1; -2\rbrace$
Gleichung 2
$\begin{array}{lllll} & 3x^2+6x+6 &=& 0 & \vert :3 \\ & x^2+2x+2 &=& 0 & \\ \end{array}$
Mit den Koeffizienten $p=2$ und $q=2$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 22\pm\sqrt{\frac {2^2}4-2} \\ & x_{1,2} &=& - 1\pm\sqrt{1-2} \\ & x_{1,2} &=& - 1\pm\sqrt{-1} \end{array}$
Da der Ausdruck unter der Wurzel negativ ist, hat diese quadratische Gleichung keine Lösung. Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace \rbrace$. Sie ist also leer.
-
Ermittle die Lösungen der quadratischen Gleichungen.
TippsAlle quadratischen Gleichungen liegen in der Normalform vor. Du kannst also die $pq$-Formel direkt verwenden:
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
Sieh dir folgendes Beispiel an: $~x^2\ \underbrace{-4}_{p}\ x\ \underbrace{-5}_{q}\ =\ 0$
$\begin{array}{llll} & x_{1,2} &=& -\frac {-4}2\pm\sqrt{\frac {-4^2}4-(-5)} \\ & x_{1,2} &=& 2\pm\sqrt{4+5} \\ & x_{1,2} &=& 2\pm\sqrt{9} \\ & x_{1,2} &=& 2\pm 3 \\ \\ & x_1 &=& 5 \\ & x_2 &=& -1 \end{array}$
LösungWir setzen die Koeffizienten $p$ und $q$ aus der Normalform $x^2+px+q=0$ und die $pq$-Formel ein:
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
Gleichung 1: $~x^2 + 2x + 1 = 0$
Mit den Koeffizienten $p=2$ und $q=1$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 22\pm\sqrt{\frac {2^2}4-1} \\ & x_{1,2} &=& -1\pm\sqrt{1-1} \\ & x_{1,2} &=& -1\pm\sqrt{0} \\ & x_{1,2} &=& -1\pm 0 \\ \\ & x &=& -1 \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -1\rbrace$
Gleichung 2: $~x^2 + 10x + 9 = 0$
Mit den Koeffizienten $p=10$ und $q=9$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac {10}2\pm\sqrt{\frac {10^2}4-9} \\ & x_{1,2} &=& -5\pm\sqrt{25-9} \\ & x_{1,2} &=& -5\pm\sqrt{16} \\ & x_{1,2} &=& -5\pm 4 \\ \\ & x_1 &=& -1 \\ & x_2 &=& -9 \\ \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -1; -9\rbrace$
Gleichung 3: $~x^2 + 8x + 7 = 0$
Mit den Koeffizienten $p=8$ und $q=7$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac {8}2\pm\sqrt{\frac {8^2}4-7} \\ & x_{1,2} &=& -4\pm\sqrt{16-7} \\ & x_{1,2} &=& -4\pm\sqrt{9} \\ & x_{1,2} &=& -4\pm 3 \\ \\ & x_1 &=& -1 \\ & x_2 &=& -7 \\ \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -1; -7\rbrace$
Gleichung 4: $~x^2 + 8x -9 = 0$
Mit den Koeffizienten $p=8$ und $q=-9$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac {8}2\pm\sqrt{\frac {8^2}4-(-9)} \\ & x_{1,2} &=& -4\pm\sqrt{16+9} \\ & x_{1,2} &=& -4\pm\sqrt{25} \\ & x_{1,2} &=& -4\pm 5 \\ \\ & x_1 &=& 1 \\ & x_2 &=& -9 \\ \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace 1; -9\rbrace$
-
Erschließe die Lösungen der quadratischen Gleichungen.
TippsBringe die Gleichungen in die Normalform, indem du sie jeweils durch den Koeffizienten ihres quadratischen Gliedes teilst.
Beachte die Vorzeichen der Koeffizienten.
Sieh dir folgendes Beispiel an: $~-\frac 15x^2 + 3x + 6 = 0$
Diese Gleichung überführst du in die Normalform, indem du entweder durch $-\frac 15$ teilst oder mit $-5$ multiplizierst.
LösungWir überführen die quadratischen Gleichungen in die Normalform, indem wir die Gleichungen jeweils durch den Koeffizienten ihres quadratischen Gliedes teilen. So erhalten wir Gleichungen in der Normalform:
- $x^2+px+q=0$
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
- $\frac {p^2}4-q>0$: zwei Lösungen
- $\frac {p^2}4-q=0$: eine Lösung
- $\frac {p^2}4-q<0$: keine Lösung
Gleichung 1
$\begin{array}{lllll} & 4x^2 + 8x -12 &=& 0 & \vert :4 \\ & x^2 + 2x -3 &=& 0 & \\ \end{array}$
Mit den Koeffizienten $p=2$ und $q=-3$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 22\pm\sqrt{\frac {2^2}4-(-3)} \\ & x_{1,2} &=& -1\pm\sqrt{1+3} \\ & x_{1,2} &=& -1\pm\sqrt{4} \\ & x_{1,2} &=& -1\pm 2 \\ \\ & x_1 &=& 1 \\ & x_2 &=& -3 \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace 1; -3\rbrace$
Gleichung 2
$\begin{array}{lllll} & -3x^2 - 6x - 3 &=& 0 & \vert :(-3) \\ & x^2 + 2x +1 &=& 0 & \\ \end{array}$
Mit den Koeffizienten $p=2$ und $q=1$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 22\pm\sqrt{\frac {2^2}4-1} \\ & x_{1,2} &=& -1\pm\sqrt{1-1} \\ & x_{1,2} &=& -1\pm\sqrt{0} \\ & x_{1,2} &=& -1\pm 0 \\ \\ & x &=& -1 \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -1\rbrace$
Gleichung 3
$\begin{array}{lllll} & \frac 12x^2 + 3x + 4 &=& 0 & \vert \cdot 2 \\ & x^2 + 6x + 8 &=& 0 & \\ \end{array}$
Mit den Koeffizienten $p=6$ und $q=8$ folgt:
$\begin{array}{llll} & x_{1,2} &=& -\frac 62\pm\sqrt{\frac {6^2}4-8} \\ & x_{1,2} &=& -3\pm\sqrt{9-8} \\ & x_{1,2} &=& -3\pm\sqrt{1} \\ & x_{1,2} &=& -3\pm 1 \\ \\ & x_1 &=& -2 \\ & x_2 &=& -4 \end{array}$
Damit lautet die Lösungsmenge: $\mathbb{L}=\lbrace -2; -4\rbrace$
-
Gib den Zusammenhang zwischen der Anzahl der Lösungen einer quadratischen Gleichung und der Diskriminante der $pq$-Formel an.
TippsDie $pq$-Formel lautet:
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
Es gilt:
- $\left(\dfrac ab\right)^2=\dfrac{a^2}{b^2}$
Bedenke, dass du aus negativen Zahlen keine Wurzel ziehen kannst, wenn du nur mit reellen Zahlen rechnest.
LösungDie $pq$-Formel lautet:
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
- $x_{1,2}=-\frac p2\pm\sqrt{\left(\frac p2\right)^2-q}$
- $\left(\frac p2\right)^2-q=\frac {p^2}4-q>0$: zwei Lösungen
- $\left(\frac p2\right)^2-q=\frac {p^2}4-q=0$: eine Lösung
- $\left(\frac p2\right)^2-q=\frac {p^2}4-q<0$: keine Lösung
-
Bestimme die Linearfaktorzerlegungen der quadratischen Gleichungen in Normalform.
TippsHat eine quadratische Gleichung in Normalform die Lösungen $m$ und $n$, so kannst du die Produktform dieser Gleichung wie folgt schreiben:
- $(x-m)(x-n)=0$
Du kannst deine Ergebnisse überprüfen, indem du die Klammern der Linearfaktorzerlegung ausmultiplizierst. Es gilt:
- $(a+b)(c+d)=ac+ad+bc+bd$
LösungHat eine quadratische Gleichung in Normalform die Lösungen $m$ und $n$, so kannst du die Produktform dieser Gleichung wie folgt schreiben:
- $(x-m)(x-n)=0$
- $x_{1,2}=-\frac p2\pm\sqrt{\frac {p^2}4-q}$
- $\frac {p^2}4-q>0$: zwei Lösungen
- $\frac {p^2}4-q=0$: eine Lösung
- $\frac {p^2}4-q<0$: keine Lösung
Gleichung 1: $~x^2 + 4x -12 = 0$
$\begin{array}{llll} & x_{1,2} &=& -\frac 42\pm\sqrt{\frac {4^2}4+12} \\ & x_{1,2} &=& -2\pm\sqrt{16} \\ & x_{1,2} &=& -2\pm 4 \\ \\ & x_1 &=& 2 \\ & x_2 &=& -6 \end{array}$
Die Produktform lautet dann: $~(x-2)(x+6)=0$
Gleichung 2: $~x^2 + 5x + 4 = 0$
$\begin{array}{llll} & x_{1,2} &=& -\frac 52\pm\sqrt{\frac {5^2}4-4} \\ & x_{1,2} &=& -\frac 52\pm\sqrt{\frac {25}4-\frac {16}4} \\ & x_{1,2} &=& -\frac 52\pm\sqrt{\frac 94} \\ & x_{1,2} &=& -\frac 52\pm\frac 32 \\ \\ & x_1 &=& -1 \\ & x_2 &=& -4 \end{array}$
Die Produktform lautet dann: $~(x+1)(x+4)=0$
Gleichung 3: $~x^2 + 8x - 9 = 0$
$\begin{array}{llll} & x_{1,2} &=& -\frac 82\pm\sqrt{\frac {8^2}4+9} \\ & x_{1,2} &=& -4\pm\sqrt{25} \\ & x_{1,2} &=& -4\pm 5 \\ \\ & x_1 &=& 1 \\ & x_2 &=& -9 \end{array}$
Die Produktform lautet dann: $~(x-1)(x+9)=0$
8.906
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.867
Lernvideos
37.599
Übungen
33.716
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
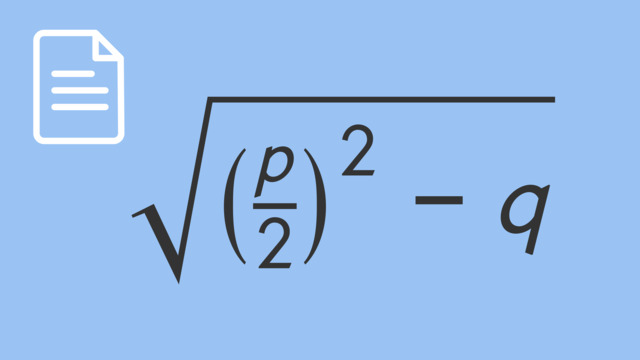
rehh
Hallo Markus Schewe, wahrscheinlich steht in Deiner Formelsammlung (p/2)². Durch die Klammer bezieht sich das Quadrat auch auf das 1/2. Quadriert man 1/2, erhält man ein Viertel: also insgesamt p²/4, aber ohne Klammer.
Viele Grüße aus der Redaktion
warum p/4 ich hatte das mit p/2 zum Quadrat gelernt steht auch bei uns so in der Formelsammlung?