Grenzwerte von Funktionen für x → xₒ – Testeinsetzung


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
Nach dem Schauen dieses Videos wirst du in der Lage sein, das Verfahren der Testeinsetzung zur Grenzwertbestimmung anzuwenden.

Zunächst lernst du, wie man die Definitionslücke erkennt. Anschließend werden wir die Definitionslücke genauer mit dem linksseitigen und dem rechtsseitigen Grenzwert untersuchen. Abschließend lernst du, was ein uneigentlicher Grenzwert und ein Polstelle sind.

Lerne etwas außerdem einen Funfact über die militärischen Festungsanlagen im alten Rom.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Hyperbel, Definitionslücke, Limes, Grenzwert, uneigentlicher Grenzwert und Polstelle.
Bevor du dieses Video schaust, solltest du bereits verschiedene Funktionstypen kennen und wissen, wie man den Definitionsbereich von Funktionen bestimmt.
Transkript Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
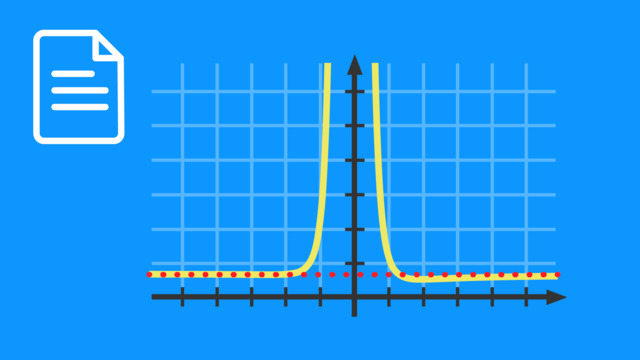
Wusstest du, dass der Limes der alten Römer es bis in die heutige Mathematik geschafft hat? Dieser militärische Grenzwall sicherte das römische Reich gegen Angriffe von außen ab. In der Mathematik ist der Limes ein anderer Begriff für den Grenzwert. Also bewaffne dich mit Stift und Papier, denn jetzt geht es um „Grenzwerte von Funktionen“. Du kennst schon alle möglichen Funktionen. Zu einer Funktion gehört immer auch ihr Definitionsbereich. Das sind alle x-Werte, die wir in die Funktionsgleichung einsetzen können, um einen Funktionswert auszurechnen. Bei diesen Beispielen können wir alle beliebigen reellen Zahlen von minus unendlich bis plus unendlich einsetzen, und erhalten immer einen Funktionswert. Es gibt aber auch spezielle Funktionen, die man mit Samthandschuhen anfassen muss. Zum Beispiel diese Hyperbel. Wenn man hier eine falsche Zahl für x einsetzt, würde man eine Division durch null kreieren und damit die mathematische Welt aus ihren Angeln heben. Um das zu vermeiden, wird die drei aus dem Definitionsbereich ausgeschlossen. Die Funktion hat an der Stelle „x gleich drei“ folglich keinen Funktionswert. Man nennt diese Stelle dann auch Definitionslücke und kann sie mit „x null“ bezeichnen. Da man eine Funktion nicht direkt in „x null“ untersuchen kann, nähert man sich dieser Stelle vorsichtig mit dem Limes. Der Limes beschreibt, was passiert, wenn man für eine Variable Werte einsetzt, die einem bestimmten Wert immer näher kommen. Das schreibt man so auf: Der Limes von „x gegen x null“ der Funktion „f von x“. Unter dem Limes stehen also die Variable und der Wert, dem sie immer näher kommt. In unserem Fall also Limes von „x gegen drei“ von „eins durch x minus drei“. Ist das Ergebnis eine reelle Zahl, dann wird diese Zahl g „Grenzwert der Funktion f an der Stelle x null“ genannt. Das schauen wir uns bei unserem Beispiel jetzt genauer an. Wir wollen also herausfinden, wie sich die Funktion an der Definitionslücke verhält. Den kritischen Wert „x null gleich drei“ dürfen wir zwar nicht einsetzen, aber wir dürfen alle Zahlen einsetzen, die minimal von der Drei abweichen. Und genau das machen wir uns bei der Testeinsetzung zunutze. Dafür betrachten wir die Definitionslücke der Funktion von zwei Seiten, einmal von links und einmal von rechts.
Beim linksseitigen Grenzwert untersuchen wir die x-Werte, die minimal kleiner sind als drei, und beim rechtsseitigen Grenzwert die Zahlen, die minimal größer sind als drei. Dafür stellen wir eine Wertetabelle auf, in der wir die x-Werte aufschreiben, die sich immer dichter an drei annähern. Dann können wir die zugehörigen Funktionswerte berechnen. Anhand der Tabelle ist erkennbar, dass die Funktionswerte immer kleiner werden. Der linksseitige Grenzwert geht also gegen minus Unendlich. Das ist natürlich keine reelle Zahl. Wir sprechen deshalb von einem uneigentlichen Grenzwert. Schauen wir uns nun den rechtsseitigen Grenzwert an, indem wir die x-Werte betrachten, die minimal größer sind als drei. Auch hier stellen wir wieder eine Wertetabelle auf. Dieses Mal werden die x-Werte immer kleiner und nähern sich der drei an. Pausiere doch kurz das Video und berechne selbst die fehlenden Funktionswerte. Du siehst: Hier werden die Funktionswerte immer größer. Der rechtsseitige Grenzwert geht also gegen plus unendlich. Auch das ist natürlich ein uneigentlicher Grenzwert. Der linksseitige Grenzwert ist also minus unendlich und der rechtsseitige Grenzwert plus unendlich. Wenn es sich um uneigentliche Grenzwerte handelt, nennt man die Stelle „x null“ Polstelle. Das kann man natürlich auch schnell erkennen, wenn man sich den Verlauf des Graphen noch einmal genau anschaut. Hier kann man die Polstelle als senkrechte Asymptote gut erkennen. Ein uneigentlicher Grenzwert - sowas kann einem auch nur in Mathe über den Weg laufen. Schauen wir uns deshalb noch ein zweites Beispiel an. Welchen Wert darf man bei dieser Funktion nicht einsetzen? Nun, der Nenner darf nie Null werden. Schauen wir also einmal, bei welchem x-Wert wir für den Nenner null erhalten. Wenn wir die Gleichung nach x umstellen, bekommen wir als Definitionslücke „x null gleich zwei“ heraus. Diese Stelle wird deshalb im Definitionsbereich ausgeschlossen. Jetzt gehen wir wieder mit dem linksseitigen, und rechtsseitigen Grenzwert vorsichtig an diese Stelle heran und schauen, wie sich die Funktionswerte in dieser Umgebung verhalten. Dafür führen wir wieder unsere Testeinsetzungen durch. Diesmal für die x-Werte die sich von links der Definitionslücke „x null gleich zwei“ annähern, und für die x-Werte, die sich von der rechten Seite der Zwei annähern. Mit scharfem Blick auf die Ergebnisse erkennen wir, dass sich sowohl der linksseitige, als auch der rechtsseitige Grenzwert immer weiter an die vier annähern. In diesem Fall stimmen beide Grenzwerte überein, und wir sprechen von einer hebbaren Definitionslücke an der Stelle „x null gleich zwei“. Wenn man die Funktion nun zeichnet, macht man die hebbare Definitionslücke durch einen leeren Kreis deutlich. Gut, dass wir diese Wissenslücke nun schließen konnten. Dann können wir ja zusammenfassen. Den Grenzwert einer Funktion an einer Stelle „x null“ kann man mithilfe von Testeinsetzungen untersuchen. Dabei ist die entsprechende Stelle „x null“ entweder schon vorgegeben oder die Definitionslücke einer gebrochen rationalen Funktion muss selbst bestimmt werden. Dazu setzt man den Nenner des Funktionsterms gleich null. Danach wird der linksseitige und der rechtsseitige Grenzwert aufgestellt. Anschließend kann man die Testeinsetzungen ausführen und in einer Wertetabelle festhalten. Ist der links- und der rechtsseitige Grenzwert eine identische, reelle Zahl, spricht man von einer hebbaren Definitionslücke. Gehen die Grenzwerte nach plus oder minus unendlich, liegt eine Polstelle vor. Wenn du das alles verstanden hast, findest du diesen Joke sicher auch grenzwertig witzig.
Grenzwerte von Funktionen für x → xₒ – Testeinsetzung Übung
-
Benenne die einzelnen Elemente in der Limes-Schreibweise.
TippsAn einer Definitionslücke besitzt eine Funktion keinen Funktionswert.
LösungIst eine Funktion an einem Punkt nicht definiert, dann kann man sie nicht direkt an dieser Definitionslücke untersuchen. Daher nähert man sich dieser Stelle mit Grenzwerten an.
Dazu verwendet man die Limes-Schreibweise, welche du in der Abbildung siehst:
- Wir kürzen den Limes mit lim ab.
- Unter dem Limes stehen die Variable $x$ und der Wert, dem wir uns nähern wollen, das ist die Definitionslücke des Funktionsterms. In unserem Beispiel liegt diese bei $x = 2$.
- Darunter erkennen wir, ob es sich bei dem Ergebnis $4$ um einen linksseitigen oder einen rechtsseitigen Grenzwert handelt. In unserem Beispiel gilt $x>2$, wir nähern uns dem Wert also von rechts, daher steht das Ergebnis $4$ für den rechtsseitigen Grenzwert.
- Hinter dem Limes steht der Funktionsterm, in unserem Beispiel $\frac{x^2-4}{x-2}$.
-
Vervollständige die Testeinsetzung zur Bestimmung des linksseitigen Grenzwertes.
TippsSetze in den Funktionsterm $\frac{x^2-4}{x-2}$ die einzelnen $x$-Werte ein.
Beispiel:
Wir setzen $x=1,8$ in die Funktionsgleichung $\frac{x^2-4}{x-2}$ ein und erhalten:
$f(1,8) = \frac{1,8^2-4}{1,8-2} = \frac{-0,76}{-0,2} = 3,8$
LösungBei einigen Funktionen gibt es bestimmte $x$-Werte, welche man nicht in die Funktionsgleichung einsetzen darf. Man spricht dann von einer Definitionslücke. Die Funktion hat an dieser Stelle keinen Funktionswert.
Da man eine Funktion nicht direkt an einer Definitionslücke untersuchen kann, nähert man sich dieser Stelle mit dem Limes.In unserem Beispiel lautet die Funktion $f(x)=\frac{x^2-4}{x-2}$.
Da wir nicht durch Null teilen dürfen, also der Nenner nicht Null sein darf, hat die Funktion bei $x_0=2$ eine Definitionslücke.
Wir nähern uns nun von links der Definitionslücke. Dazu setzen wir die gegebenen $x$-Werte in die Funktionsgleichung ein und erhalten:$x=1,5 \quad f(x)=\frac{x^2-4}{x-2} = \frac{1,5^2-4}{1,5-2} = \frac{-1,75}{-0,5} = 3,5$
$x=1,9 \quad f(x)=\frac{x^2-4}{x-2} = \frac{1,9^2-4}{1,9-2} = \frac{-0,39}{-0,1} = 3,9$
$x=1,99 \quad f(x)=\frac{x^2-4}{x-2} = \frac{1,99^2-4}{1,99-2} = \frac{-0,0399}{-0,01} = 3,99$
$x=1,999 \quad f(x)=\frac{x^2-4}{x-2} = \frac{1,999^2-4}{1,999-2} = \frac{-0,003999}{-0,001} = 3,999$
Wir erkennen, dass die Funktionswerte gegen $4$ gehen. Dies ist der linksseitige Grenzwert. -
Bestimme den Definitionsbereich der Funktionen.
TippsBestimme jeweils zuerst die Definitionslücke. Dazu muss der Nenner gleich Null gesetzt werden.
Beispiel:
$f(x)=\frac{x}{x-4}$
$\mathbb{D}=x \in \mathbb{R}, x \neq 4$
LösungBei gebrochenrationalen Funktionen enthält der Funktionsterm einen Bruch. Es kann daher sein, dass für bestimmte Werte von $x$ eine Null im Nenner dieses Bruchs entsteht. Da es in der Mathematik nicht erlaubt ist durch Null zu teilen, ist die Funktion für diese Werte nicht definiert. Wir nennen sie Definitionslücken.
Um den Definitionsbereich, also alle $x$-Werte, für die der Funktionsterm definiert ist, zu bestimmen, müssen wir uns zunächst überlegen, ob es Definitionslücken gibt. Dazu bestimmen wir die Nullstellen des Nenners.
Der Definitionsbereich enthält dann alle rationalen Zahlen, außer den Definitionslücken ($d_1, d_2, ...$). Wir schreiben:
$\mathbb{D}=x \in \mathbb{R}, x \neq d_1, x \neq d_2, ...$Wir bestimmen also jeweils zuerst die Definitionslücke, indem wir die Nullstelle(n) des Nenners berechnen und geben dann den Definitionsbereich an:
Beispiel 1: $f(x)=\frac{x}{x-1}$
Nullstelle des Nenners: $x-1=0 \Leftrightarrow x=1$
Definitionslücke: $x_0=1$
Definitionsbereich: $\mathbb{D}=x \in \mathbb{R}, x \neq 1$Beispiel 2: $f(x)=\frac{x+3}{x^2-1}$
Nullstellen des Nenners: $x^2-1=0 \Leftrightarrow x=\pm 1$
Definitionslücken: $x_1=1$ und $x_2=-1$
Definitionsbereich: $\mathbb{D}=x \in \mathbb{R}, x \neq 1, x \neq -1$Beispiel 3: $f(x)=\frac{5}{x+1}-1$
Nullstelle des Nenners: $x+1=0 \Leftrightarrow x=-1$
Definitionslücke: $x_0=-1$
Definitionsbereich: $\mathbb{D}=x \in \mathbb{R}, x \neq -1$Beispiel 4: $f(x)=\frac{3x}{x^2}$
Nullstelle des Nenners: $x^2=0 \Leftrightarrow x=0$
Definitionslücke: $x_0=0$
Definitionsbereich: $\mathbb{D}=x \in \mathbb{R}, x \neq 0$ -
Ermittle das Verhalten der Funktion an der Definitionslücke.
TippsDu kannst den linksseitigen und rechtsseitigen Grenzwert mithilfe einer Testeinsetzung bestimmen.
Wenn die Funktionswerte bei der Texteinsetzung immer größer oder immer kleiner werden, dann geht der Grenzwert gegen $+\infty$ oder $-\infty$.
LösungDefinitionslücken treten immer dann auf, wenn bestimmte $x$-Werte nicht in die Funktionsgleichung eingesetzt werden dürfen. Die Definitionslücken einer gebrochenrationalen Funktion ergeben sich aus den Nullstellen des Nenners.
Beispiel 1:
Um die Definitionslücke unserer Funktion $f(x)=\frac{x^2-1}{x-1}+1$ zu bestimmen, berechnen wir die Nullstelle des Nenners:
$x-1=0 \Leftrightarrow x=1$
Die Definitionslücke liegt bei $x_0=1$.Wir können nun den linksseitigen Grenzwert durch eine Testeinsetzung bestimmen: $\begin{array}{l|c} x& \text{Funktionswert} \\ \hline 0,5 & 2,5 \\ 0,9 & 2,9 \\ 0,99 & 2,99 \end{array}$
Wir erkennen, dass sich die Funktionswerte dem Wert $3$ annähern.Um den rechtsseitigen Grenzwert zu ermitteln, führen wir ebenfalls eine Testeinsetzung durch: $\begin{array}{l|c} x& \text{Funktionswert} \\ \hline 1,5 & 3,5 \\ 1,1 & 3,1 \\ 1,01 & 3,01 \end{array}$
Wir erkennen, dass sich auch hier die Funktionswerte dem Wert $3$ annähern.Insgesamt gilt somit: $\lim\limits_{x \to 1} = 3$.
Da der linksseitige und der rechtsseitige Grenzwert die gleiche reelle Zahl sind, sprechen wir von einer hebbaren Definitionslücke.
Beispiel 2:
Um die Definitionslücke unserer Funktion $f(x)=\frac{12}{x+3}$ zu bestimmen, berechnen wir die Nullstelle des Nenners:
$x+3=0 \Leftrightarrow x=-3$
Die Definitionslücke liegt bei $x_0=-3$.Wir können nun den linksseitigen Grenzwert durch eine Testeinsetzung bestimmen: $\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -3,5 & -24 \\ -3,1 & -120 \\ -3,01 & -1200 \end{array}$
Wir erkennen, dass die Funktionswerte immer kleiner werden. Sie nähern sich also $-\infty$.Um den rechtsseitigen Grenzwert zu ermitteln, führen wir ebenfalls eine Testeinsetzung durch: $\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -2,5 & 24 \\ -2,9 & 120 \\ -2,99 & 1200 \end{array}$
Wir erkennen, dass die Funktionswerte immer größer werden. Sie nähern sich also $+\infty$.Der rechtsseitige und der linksseitige Grenzwert gehen gegen $-\infty$ bzw. $+\infty$, daher liegt eine Polstelle vor.
-
Beschreibe, was man unter einer Definitionslücke versteht.
TippsIn der Mathematik darf nicht durch Null geteilt werden.
Bruch: $\quad \dfrac{\text{Zähler}}{\text{Nenner}}$
LösungDefinitionslücken treten in der Mathematik dann auf, wenn bestimmte $x$-Werte nicht in einen Funktionsterm eingesetzt werden dürfen. Die Funktion hat an dieser Stelle keinen Funktionswert. Die Aussage 'Eine Definitionslücke ist eine Stelle, an der eine Funktion keinen Funktionswert hat.' ist also richtig.
Gebrochenrationale Funktionen enthalten einen Bruch im Funktionsterm. In der Mathematik darf nicht durch Null geteilt werden. Daher darf der Nenner nicht Null ergeben. Die Denfinitionslücken entsprechen also den Nennernullstellen. Die Aussage 'Die Definitionslücken einer gebrochenrationalen Funktion ergeben sich aus den Nullstellen des Zählers.' ist somit falsch.
Der Definitionsbereich gibt an, welche $x$-Werte in die Funktionsgleichung eingesetzt werden dürfen. Er enthält also alle $x$-Werte, für die die Funktion definiert ist. Die Aussage 'Der Definitionsbereich enthält alle $y$-Werte, die möglich sind.' ist also falsch, es handelt sich nämlich um die $x$-Werte.
'Um zu untersuchen, wie sich eine Funktion in der Nähe einer Definitionslücke verhält, nähert man sich dieser mit Hilfe des Grenzwertes.' Diese Aussage ist richtig.
-
Untersuche, ob die Funktion eine Polstelle, eine hebbare Definitionslücke oder keines von beiden besitzt.
TippsBestimme jeweils zuerst die Definitionslücke, falls vorhanden.
Um zu entscheiden, ob es sich um eine hebbare Definitionslücke oder eine Polstelle handelt, musst du den linksseitigen und den rechtsseitigen Grenzwert bestimmen.
Führe dazu eine Testeinsetzung durch.LösungHat eine Funktion eine Definitionslücke, so unterscheiden wir zwischen hebbaren Definitionslücken und Polstellen.
Wir untersuchen zunächst die gegebenen Funktionen auf Definitionslücken:
Folgende Funktionen haben keine Definitionslücke, alle $x \in \mathbb{R}$ dürfen eingesetzt werden:
- $f(x)=x^2+1$
- $f(x)=-3 \cdot 4^x$
- $f(x)=\frac{5x}{x+2} \quad$ $x+2=0 \Leftrightarrow x=-2 \quad$ Definitionslücke: $x_0=-2$
- $f(x)=\frac{x^2+9}{x+3} \quad$ $x+3=0 \Leftrightarrow x=-3 \quad$ Definitionslücke: $x_0=-3$
- $f(x)=\frac{x^2-4}{8-4x} \quad$ $8-4x=0 \Leftrightarrow x=2 \quad$ Definitionslücke: $x_0=2$
$f(x)=\dfrac{5x}{x+2}$, Definitionslücke: $x_0=2$
Bestimmung des linksseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -2,5 & 25 \\ -2,1 & 105 \\ -2,01 & 1005 \\ \text{geht gegen} & \infty \\ \end{array}$Bestimmung des rechtsseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -1,5 & -22,5 \\ -1,9 & -180,5 \\ -1,99 & -1980,05 \\ \text{geht gegen} & -\infty \\ \end{array}$Der rechtsseitige und der linksseitige Grenzwert gehen gegen $-\infty$ bzw. $+\infty$, daher liegt eine Polstelle vor.
$f(x)=\dfrac{x^2+9}{x+3}, $ Definitionslücke: $x_0=-3$
Bestimmung des linksseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -3,5 & 6,5 \\ -3,1 & 6,1 \\ -3,01 & 6,01 \\ \text{geht gegen} & 6 \\ \end{array}$Bestimmung des rechtsseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline -2,5 & 5,5 \\ -2,9 & 5,9 \\ -2,99 & 5,99 \\ \text{geht gegen} & 6\\ \end{array}$Der linksseitige und der rechtsseitige Grenzwert sind hier die gleiche reelle Zahl. Insgesamt gilt: $\lim\limits_{x \to -3} \frac{x^2+9}{x+3} = 6$
Es handelt sich daher um eine hebbare Definitionslücke.$f(x)=\dfrac{x^2-4}{8-4x}$, Definitionslücke: $x_0=2$
Bestimmung des linksseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline 1,5 & -0,875 \\ 1,9 & -0,975 \\ 1,99 & -0,9975 \\ \text{geht gegen} & -1 \\ \end{array}$Bestimmung des rechtsseitigen Grenzwertes durch Testeinsetzung:
$\begin{array}{l|c} x& \text{Funktionswert} \\ \hline 2,5 & -1,125 \\ 2,1 & -1,025 \\ 2,01 & -1,0025 \\ \text{geht gegen} & -1\\ \end{array}$Der linksseitige und der rechtsseitige Grenzwert sind hier die gleiche reelle Zahl. Insgesamt gilt: $\lim\limits_{x \to -3} \frac{x^2-4}{8-4x} = -1$
Es handelt sich daher um eine hebbare Definitionslücke.

Grenzwerte von Funktionen für x → xₒ – Testeinsetzung

Grenzwerte von Funktionen für x → xₒ – Termumformung

Grenzwerte von Funktionen für x → xₒ – h-Methode

Grenzwerte x gegen unendlich – Testeinsetzung

Grenzwerte x gegen unendlich – Termvereinfachung
Ganzrationale und gebrochen rationale Funktionen – Verhalten im Unendlichen

Grenzwertsätze für Funktionen

Grenzwertsätze für Funktionen – Beispiele (1)

Grenzwertsätze für Funktionen – Beispiele (2)
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.276
Lernvideos
38.589
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung







 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?








