Grenzwerte
Testeinsetzung, h-Methode, x0-Methode, linksseitiger Grenzwert, rechtsseitiger Grenzwert, Sprungstelle, hebbare Lücken, Definitionsbereich, Polstelle
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Grenzwertberechnung
- Testeinsetzen
- Termumformung
- Die h-Methode
- Was ist der Grenzwert $x$ gegen unendlich?
- Grenzwerte von Funktionen durch Testeinsetzungen berechnen
- Beispiel 1
- Beispiel 2
Grenzwertberechnung
Die Grenzwertberechnung $\lim\limits_{x\to x_{0}} f(x)$ findet zum einen Anwendung bei der Untersuchung des Verhaltens von Funktionsgraphen von Funktionen mit Definitionslücken. Zum anderen wird diese Grenzwertberechnung verwendet zur Definition der Ableitung einer Funktion an einer Stelle $x_{0}$:
$f'(x_{0})=\lim\limits_{x\to x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}$
Es gibt verschiedene Möglichkeiten, einen solchen Grenzwert zu berechnen. Diese siehst du hier im Überblick:
- Testeinsetzen
- Termumformung
- h-Methode
Jedes dieser Verfahren schauen wir uns nun an Beispielen an.
Übrigens: Wenn die stetige Funktion $f$ für $x=x_{0}$ definiert ist, gilt $\lim\limits_{x\to x_{0}} f(x)=f\left(x_{0}\right)$.
Testeinsetzen
Gegeben ist die gebrochenrationale Funktion $f$ mit $f(x)=\frac{x^{2}-1}{x-1}$ mit dem Definitionsbereich $\mathbb{D}=\mathbb{R}\setminus\{1\}$. Du sollst überprüfen, wie sich der Funktionsgraph an der Definitionslücke $x_{0}=1$ verhält.
Hierfür untersuchst du den Grenzwert $\lim\limits_{x\to 1}\frac{x^{2}-1}{x-1}$.
Bei der Methode des Testeinsetzens wählst du eine Folge, die gegen $1$ geht, zum Beispiel $0,9$; $0,99$; $0,999$; ... Wenn du die Anzahl der $9$-en hinter dem Komma immer weiter erhöhst, geht diese Folge gegen $1$. Du setzt nun diese verschiedenen $x$-Werte in die Funktionsgleichung ein:
$\begin{array}{c|c|c|c|c|c} x&0,9&0,99&0,999&0,9999&\to 1\\ \hline f(x)&1,9&1,99&1,999&1,9999&\to 2 \end{array}$
Da die Folge sich von links an $1$ annähert, spricht man hier von dem linksseitigen Grenzwert. Ebenso kannst du den rechtsseitigen Grenzwert berechnen. Dieser ist bei diesem Beispiel übrigens ebenfalls $2$.
Wenn links- und rechtsseitiger Grenzwert endlich sind und übereinstimmen, wird die Definitionslücke, in diesem Beispiel $x_{0}=1$, als behebbar bezeichnet.
Behebbare Definitionslücken werden im Funktionsgraphen ausgeschlossen. Dies kannst du zum Beispiel durch einen Kreis andeuten. Hier siehst du den Funktionsgraphen zu der oben angegebenen Funktion.
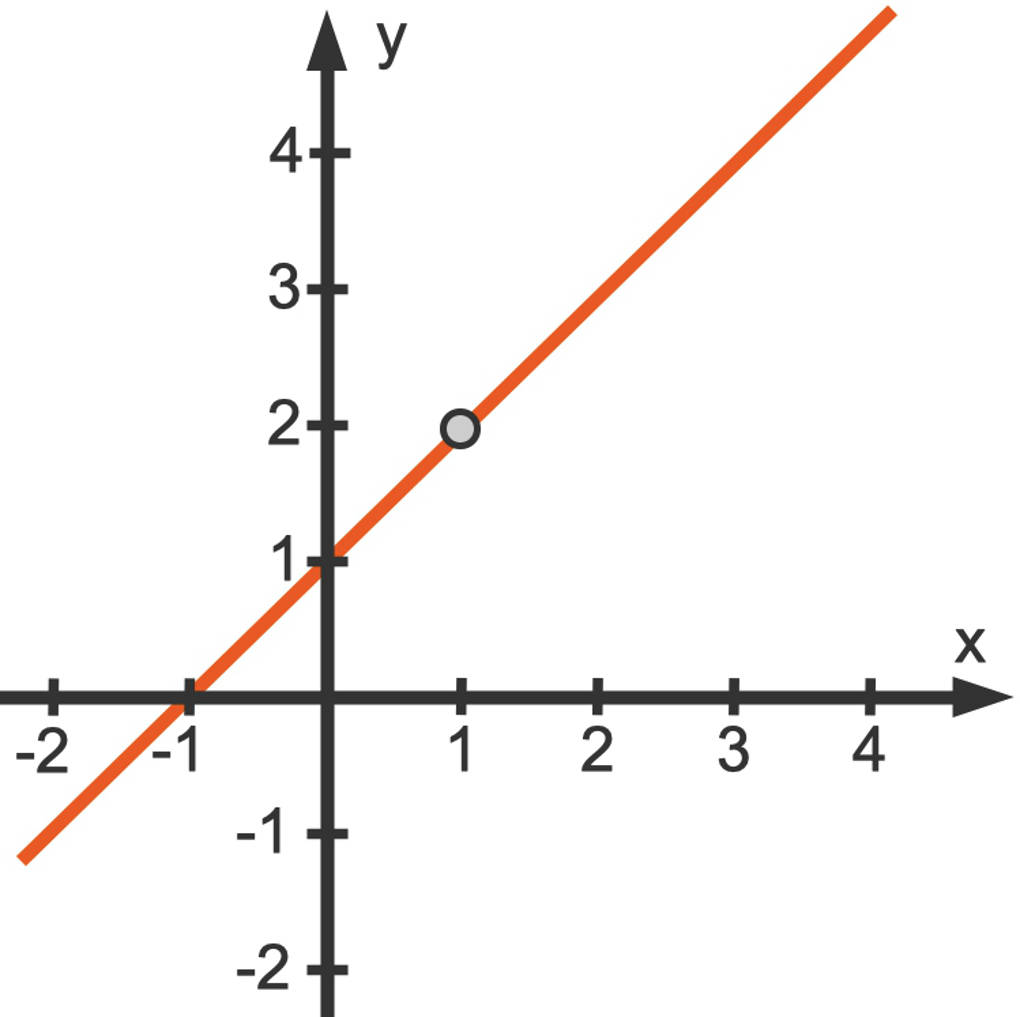
Es gibt auch Beispiele, bei welchen links- und rechtsseitiger Grenzwert ebenfalls endlich sind, allerdings nicht übereinstimmen. In diesem Fall liegt eine Sprungstelle des Funktionsgraphen vor.
Das Verfahren des Testeinsetzens kannst du übrigens auch bei Grenzwertbetrachtungen „$x\to\pm \infty$“ verwenden.
Termumformung
Bei der Termumformung kannst du entweder eine binomische Formel verwenden oder die Polynomdivision.
Dieses Verfahren siehst du nun am Beispiel der Ableitung der Funktion $f$ mit $f(x)=x^{2}-2x$.
Es ist
- $f'(x_{0})=\lim\limits_{x\to x_{0}}\frac{x^{2}-2x-\left(x_{0}^2-2x_{0}\right) }{x-x_{0}}$
- Sortiere die Terme rechts des Gleichheitszeichens zu $\lim\limits_{x\to x_0}\frac{x^2-x_0^2-\left(2x-2x_0\right)}{x-x_0}$.
- Wende eine Grenzwertregel an sowie die 3. binomische Formel: $\lim\limits_{x\to x_0}\frac{x^2-x_0^2}{x-x_0}-\lim\limits_{x\to x_0}\frac{2x-2x_0}{x-x_0}=\lim\limits_{x\to x_0}\frac{\left(x+x_0\right)\left(x-x_0\right)}{x-x_0}-\lim\limits_{x\to x_0}\frac{2x-2x_0}{x-x_0}$
- Nun kannst du jeweils $x-x_0$ kürzen zu $\lim\limits_{x\to x_0}\left(x+x_0\right)-\lim\limits_{x\to x_0}2=2x_0-2$.
Insgesamt erhältst du somit $f'(x_0)=2x_0-2$.
Wenn du keine binomische Formel anwenden kannst, um den Bruchterm zu kürzen, kannst du auch die Polynomdivision verwenden.
Du kannst in der oben gegebenen gebrochenrationalen Funktion $f$ mit $f(x)=\frac{x^{2}-1}{x-1}$ auch die 3. binomische Formel anwenden. Dann erhältst du durch Kürzen $f(x)=x+1$. Mit dieser Funktionsgleichung erhältst du ebenfalls den oben berechneten Grenzwert $\lim\limits_{x\to 1}f(x)=1+1=2$.
Die h-Methode
Anstatt den Grenzwert „$\lim\limits_{x\to x_0}$“ zu betrachten, kannst du auch „$x=x_0+h$“ betrachten und damit den Grenzwert „$\lim\limits_{h\to 0}$“. Da in diesem Verfahren $h$ betrachtet wird, spricht man von der h-Methode.
Dieses Verfahren wenden wir auf das obige Beispiel an:
$f'(x_{0})=\lim\limits_{h\to 0}\frac{\left(x_0+h\right)^{2}-2(x_0+h)-\left(x_{0}^2-2x_{0}\right) }{h}$
Du siehst, diese Rechnung sieht so ähnlich aus wie die obige. Dabei ist $x$ durch $x_0+h$ ersetzt worden.
Und los geht's:
- Wende die 1. binomische Formel an: $\lim\limits_{h\to 0}\frac{x_0^2+2\cdot x_0\cdot h+h^2-2x_0-2h-x_{0}^2+2x_{0}}{h}$.
- Nun kannst du die Terme im Zähler zusammenfassen zu $\lim\limits_{h\to 0}\frac{2\cdot x_0\cdot h+h^2-2h}{h}$.
- Klammere im Zähler $h$ aus und kürze dann mit $h$: $\lim\limits_{h\to 0}\frac{h\left(2x_0+h-2\right)}{h}=\lim\limits_{h\to 0}\left(2x_0+h-2\right)$.
- Zuletzt kannst du die einzelnen Summanden betrachten und deren Grenzwerte berechnen. So erhältst du $f'(x_0)=2x_0-2$.
So, nun ist es an dir zu entscheiden, welches der Verfahren dir am besten gefällt.
Ein Hinweis noch: Das Verfahren des Testeinsetzens ist mathematisch nicht 100 % korrekt. Es könnte ja sein, dass du zufällig eine Folge für $x$ gefunden hast, welche den errechneten Grenzwert hat. Eine andere könnte einen anderen Grenzwert haben. Das Verfahren kannst du trotzdem bedenkenlos anwenden, da es in den von dir betrachteten Fällen zu dem tatsächlichen Grenzwert führt.
Was ist der Grenzwert $x$ gegen unendlich?
Im Rahmen einer Kurvendiskussion musst du den Funktionsgraphen einer Funktion zeichnen. Genauer: Du zeichnest einen Ausschnitt des Funktionsgraphen. Dann bleibt immer noch die Frage, wie sich die Funktion außerhalb dieses Ausschnittes verhält. Welche Funktionswerte werden angenommen, wenn $x$ immer größer oder immer kleiner wird?
Mathematisch drückt man dies so aus:
- $\lim\limits_{x\to \infty}~f(x)=?$
- $\lim\limits_{x\to -\infty}~f(x)=?$
Es wird also nach dem Verhalten im Unendlichen gefragt, dem Grenzwert.
- Die Schreibweise „$\lim$“ steht für „Limes“, lateinisch für „Grenze“.
- Unter „$\lim$“ steht, wogegen $x$ gehen soll.
Im Folgenden schauen wir uns verschiedene Verfahren zum Bestimmen eines solchen Grenzwertes an.
Grenzwerte von Funktionen durch Testeinsetzungen berechnen
Bei der Grenzwertbestimmung durch Testeinsetzung gehst du wie folgt vor.
Du erstellst eine Wertetabelle. Dabei wählst du Werte für $x$, die immer größer (also $x\to \infty$) oder immer kleiner (also $x\to -\infty$) werden. Zu diesen Werten berechnest du die zugehörigen Funktionswerte. Das Verhalten dieser Funktionswerte zeigt dir dann an, wogegen die Funktionswerte schließlich gehen.
Beispiel 1
Dies schauen wir uns einmal an einem Beispiel an: $f(x)=\frac{x^2+1}{x^2}$.
Beachte, dass der Definitionsbereich dieser Funktion $\mathbb{D}_f=\mathbb{R}\setminus\{0\}$ ist. Das bedeutet, dass der Funktionsgraph an der Stelle $x=0$ eine Polstelle hat (oder haben kann!).
Den zugehörigen Funktionsgraphen kannst du hier sehen.
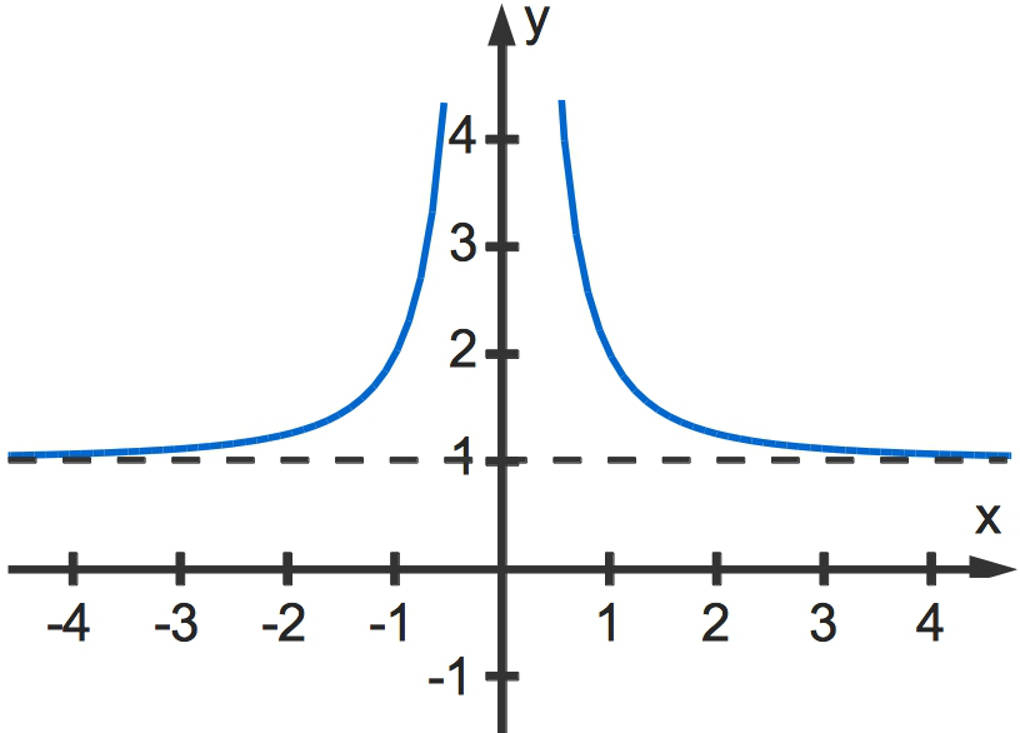
Du kannst daran auch bereits erkennen, dass sich der Funktionsgraph an eine zur $x$-Achse parallele Gerade durch $y=1$ anschmiegt.

Damit gilt:
$\lim\limits_{x\to\infty}~f(x)=1$
Ebenso kannst du den Grenzwert für $x\to-\infty$ bestimmen. Dieser ist ebenfalls $1$.
Beispiel 2
Wir schauen uns noch ein weiteres Beispiel an: $f(x)=\frac{x^2-1}{x+2}$.
Der Definitionsbereich dieser Funktion ist $\mathbb{D}_f=\mathbb{R}\setminus\{-2\}$. Hier siehst du den Teil des Funktionsgraphen für $x>-2$.
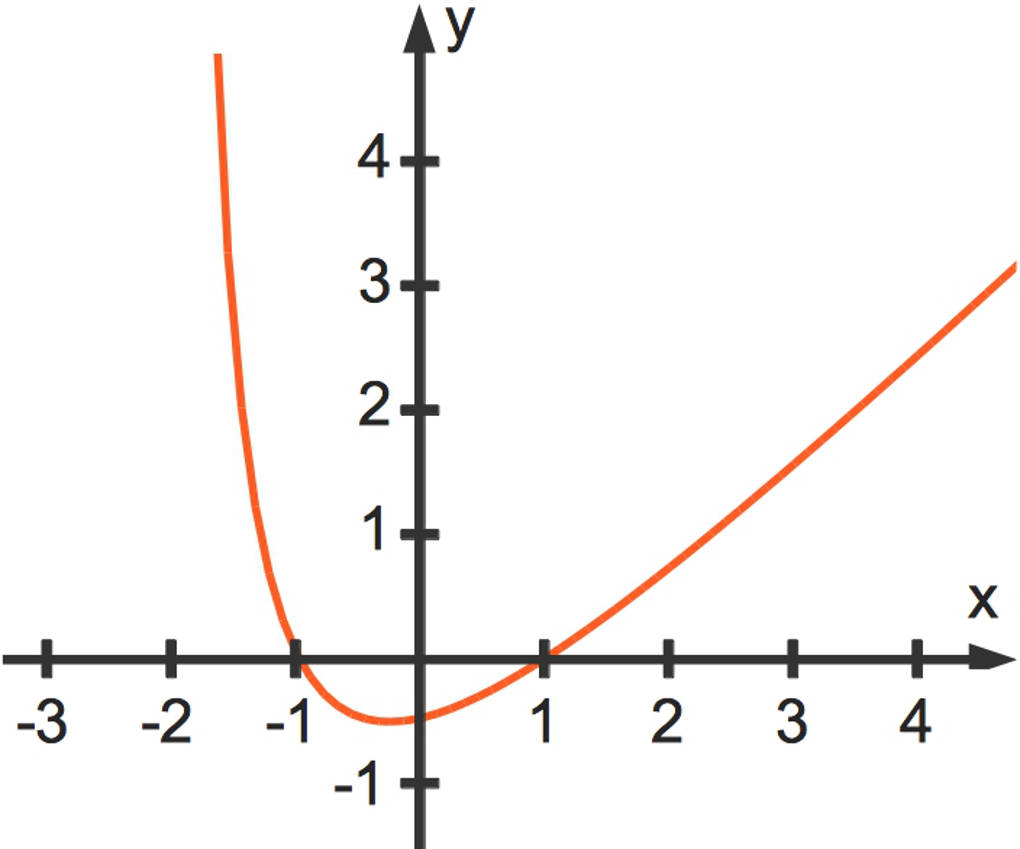
In der folgenden Wertetabelle siehst du wieder die Funktionswerte zu einigen $x$.

Du kannst sowohl an dem Funktionsgraphen als auch an der Wertetabelle erkennen, dass die Funktionswerte für immer größer werdende $x$ auch immer größer werden. Es gilt also:
$\lim\limits_{x\to\infty}~f(x)=$„$\infty$“
In diesem Fall liegt ein uneigentlicher Grenzwert, also keine endliche Zahl, vor. Deswegen schreibt man dies oft in Anführungszeichen.
Grenzwerte von Funktionen durch Termvereinfachungen berechnen
Das Verfahren durch Testeinsetzung ist streng genommen nicht korrekt. Warum? Es könnte zufällig so sein, dass du eine Folge von $x$ gefunden hast, welche gegen unendlich geht, für die der entsprechende Grenzwert für die Funktion herauskommt. Bei einer anderen Folge könnte auch der Grenzwert ein anderer sein. Dies ist allerdings bei den betrachteten Funktionen nicht der Fall.
Etwas „ mathematischer“ ist das Verfahren der Termvereinfachung oder auch Termumformung.
Hierfür schauen wir uns noch einmal das erste Beispiel an: $f(x)=\frac{x^2+1}{x^2}$.
Der Grenzwert ist bereits bekannt. Dieser ist $1$.
Der Funktionsterm wird nun umgeformt. Du kannst jeden Summanden im Zähler durch den Nenner dividieren und erhältst dann:
$f(x)=\frac{x^2+1}{x^2}=1+\frac1{x^2}$
Nun kannst du dir jeden einzelnen Summanden anschauen. Du verwendest hierfür die Grenzwertsätze.
Der Grenzwert der Summe zweier Funktionen ist gleich der Summe der Grenzwerte der einzelnen Summanden. Dies gilt ebenso für Differenzen:
$\lim\limits_{x\to\infty}(f(x)\pm g(x))=\lim\limits_{x\to\infty}f(x)\pm\lim\limits_{x\to\infty}g(x)$
Also gilt:
$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}\left(1+\frac1{x^2}\right)=\lim\limits_{x\to\infty}1+\lim\limits_{x\to\infty}\frac1{x^2}$
Der linke Grenzwert ist $1$, da eine konstante Funktion betrachtet wird, und der rechte ist $0$, also folgt insgesamt:
$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}1+\lim\limits_{x\to\infty}\frac1{x^2}=1+0=1$
Grenzwerte von ganzrationalen Funktionen
Eine ganzrationale Funktion sieht wie folgt aus:
$f(x)=a_n\cdot x^n+a_{n+1}\cdot x^{n-1}+...+a_2\cdot x^2+a_1\cdot x+a_0$
Dabei ist $n$ der Grad, die höchste Potenz, und $a_n$ der zugehörige Koeffizient der ganzrationalen Funktion.
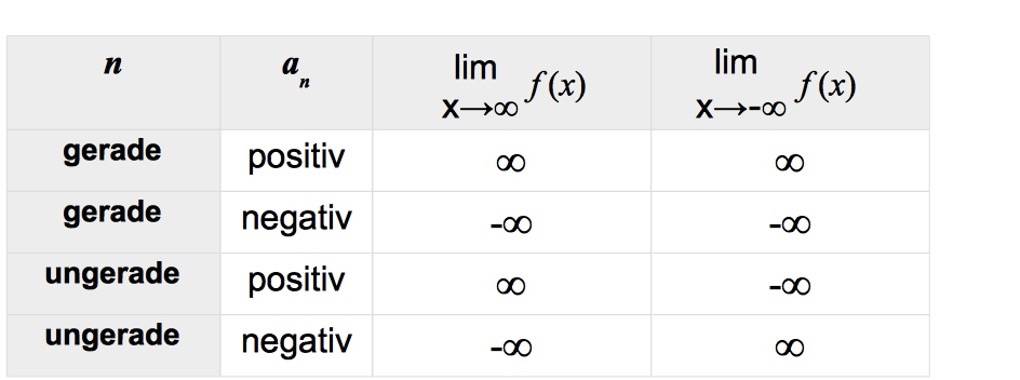
Das Grenzwertverhalten ganzrationaler Funktionen hängt
- zum einen davon ab, ob der Grad $n$ gerade oder ungerade ist und
- zum anderen davon, ob der Koeffizient $a_n$ vor dem $x$ mit der höchsten Potenz positiv oder negativ ist.
Dies schauen wir uns jeweils an einem Beispiel an.
Ganzrationale Funktionen mit geradem Grad
Es sollen die Grenzwerte für $x$ gegen plus und minus unendlich der Funktion $f(x)=x^2$ bestimmt werden. Der Funktionsgraph ist eine nach oben geöffnete Parabel.

Du kannst hier erkennen, dass sowohl für immer größer als auch für immer kleiner werdende $x$ die Funktionswerte immer größer werden, also gegen unendlich gehen. Dies kannst du natürlich durch Testeinsetzung überprüfen. Es gilt also
$\lim\limits_{x\to\infty}~f(x)=\lim\limits_{x\to-\infty}~f(x)=$„$\infty$“.
Wenn du statt $f(x)=x^2$ die Funktion $g(x)=-x^2$ betrachtest, erhältst du eine an der $x$-Achse gespiegelte, also nach unten geöffnete, Parabel. Damit gilt
$\lim\limits_{x\to\infty}~g(x)=\lim\limits_{x\to-\infty}~g(x)=$„$-\infty$“.
Ganzrationale Funktionen mit ungeradem Grad
Hierfür schauen wir uns die Funktion $f(x)=x^3$ mit dem dazugehörigen Funktionsgraphen an.
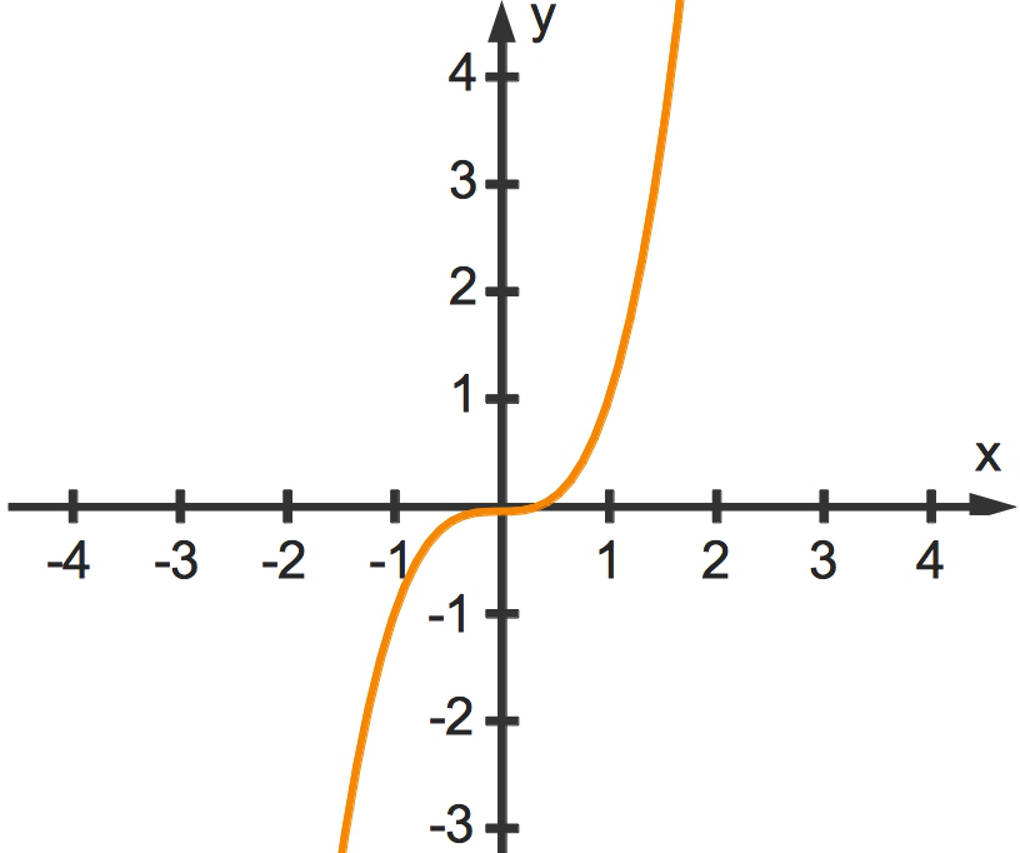
Hier kannst du die folgenden Grenzwerte erkennen:
$\lim\limits_{x\to\infty}~f(x)=$„$\infty$“ und
$\lim\limits_{x\to-\infty}~f(x)=$„$-\infty$“.
Auch hier führt die Spiegelung an der $x$-Achse zu einer Vorzeichenveränderung bei den Grenzwerten. Für $g(x)=-x^3$ gilt
$\lim\limits_{x\to\infty}~g(x)=$„$-\infty$“ sowie
$\lim\limits_{x\to-\infty}~g(x)=$„$\infty$“.
Zusammenfassung
Du siehst, je nach Grad $n$, gerade oder ungerade, und entsprechendem Koeffizienten $a_n$, positiv oder negativ, kannst du die Grenzwerte einer ganzrationalen Funktion
$f(x)=a_n\cdot x^n+a_{n+1}\cdot x^{n-1}+...+a_2\cdot x^2+a_1\cdot x+a_0$
direkt angeben. Die folgende Tabelle soll dir hierfür einen Überblick geben.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Grenzwerte (8 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grenzwerte (9 Arbeitsblätter)
-
 Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
PDF anzeigen
Grenzwerte von Funktionen für x → xₒ – Testeinsetzung
PDF anzeigen -
 Grenzwerte von Funktionen für x → xₒ – Termumformung
PDF anzeigen
Grenzwerte von Funktionen für x → xₒ – Termumformung
PDF anzeigen -
 Grenzwerte von Funktionen für x → xₒ – h-Methode
PDF anzeigen
Grenzwerte von Funktionen für x → xₒ – h-Methode
PDF anzeigen -
 Grenzwerte x gegen unendlich – Testeinsetzung
PDF anzeigen
Grenzwerte x gegen unendlich – Testeinsetzung
PDF anzeigen -
 Grenzwerte x gegen unendlich – Termvereinfachung
PDF anzeigen
Grenzwerte x gegen unendlich – Termvereinfachung
PDF anzeigen -
 Ganzrationale und gebrochen rationale Funktionen – Verhalten im Unendlichen
PDF anzeigen
Ganzrationale und gebrochen rationale Funktionen – Verhalten im Unendlichen
PDF anzeigen -
 Grenzwertsätze für Funktionen
PDF anzeigen
Grenzwertsätze für Funktionen
PDF anzeigen -
 Grenzwertsätze für Funktionen – Beispiele (1)
PDF anzeigen
Grenzwertsätze für Funktionen – Beispiele (1)
PDF anzeigen -
 Grenzwertsätze für Funktionen – Beispiele (2)
PDF anzeigen
Grenzwertsätze für Funktionen – Beispiele (2)
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




















