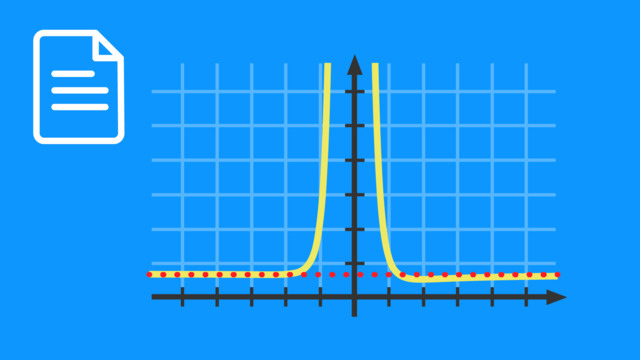
Gebrochenrationale Funktionen – Eigenschaften
Beschreibung Gebrochenrationale Funktionen – Eigenschaften
Hallo und herzlich willkommen. In diesem Video behandeln wir die wichtigsten Eigenschaften gebrochenrationaler Funktionen. Hierzu geben wir dir zuerst eine Definition einer gebrochenrationalen Funktion. Im Anschluss erklären wir dir an Beispielen, was man unter Definitionslücken versteht und welche Arten von Definitionslücken gebrochenrationale Funktionen besitzen. Zum Ende lernst du an einigen Beispielen den Begriff der Asymptote sowie die verschiedenen Arten von Asymptoten kennen. Viel Spaß!
Transkript Gebrochenrationale Funktionen – Eigenschaften
Hallo. In diesem Video geht es um wichtige Eigenschaften gebrochenrationaler Funktionen. Zunächst werden wir kurz wiederholen, was gebrochenrationale Funktionen sind. Dann stoßen wir auf ihre Definitionslücken. Das heißt, Einschränkungen an den Definitionsbereichen, weil die Funktion für bestimmte x-Werte gar nicht definiert ist. Doch, Definitionslücke ist nicht gleich Definitionslücke. Es gibt zwei Typen davon, die wir uns schauen werden. Ebenfalls charakteristisch für gebrochenrationale Funktionen sind Asymptoten. Auch davon gibt es verschiedene Typen, die wir kennenlernen werden. Was sind also gebrochenrationale Funktionen? Das sind Funktionen, die sich als Quotient von ganzrationalen Funktionen, auch Polynome genannt, schreiben lassen. Also in der Form (a0 + a1×x + a2×x2 + … +an×xn)/(b0 + b1×x + b2×x2 + … +bm×xm). Wichtig hierbei ist, dass an und bm ungleich 0 sind. Wir teilen also ein Zählerpolynom z durch ein Nennerpolynom n. Das Zählerpolynom definiert die Nullstellen der Funktion, wie ihr es von anderen Polynomen kennt. Das Nennerpolynom hingegen beeinflusst das Verhalten der Funktion. Das untersuchen wir jetzt genauer. Zunächst die Definitionslücken: Da der Nenner eines Quotienten nicht 0 werden darf, hat eine gebrochenrationale Funktion genau dann eine Definitionslücke, wenn dieser Fall eintritt. Die Nullstellen des Nenners sind also die Definitionslücken der Funktion. Zwei Beispiele: die Funktion f(x) = (x3 + 2x - 5)/(x - 3) ist für x = 3 nicht definiert. Im Definitionsbereich muss die 3 demnach ausgeschlossen werden. Der Nenner der Funktion f(x) = (3x2 - 7x + 1)/(x2 + 5) wird hingegen niemals null. Der Definitionsbereich ist ganz ℝ. Es gibt aber verschiedene Arten von Definitionslücken. “Hebbare Definitionslücken” und “Polstellen”. Worin bestehen die Unterschiede? Hebbare Definitionslücken treten dann auf, wenn Zähler- und Nennerpolynom gleichzeitig eine Nullstelle x0 haben. Und der Grenzwert der Funktion x gegen x0 existiert. Beispiel: Zähler und Nenner der Funktion f(x) = (x - 1)/(x2 - 1) werden für x=1 null. Wir wenden die dritte binomische Formel an und erhalten: (x - 1)/(x + 1)×(x - 1). Wir können nun die Nullstelle beziehungsweise den dazugehörigen Linearfaktor (x-1) wegkürzen. Der Grenzwert ist 1/2. Funktion und ihr Graph verhalten sich also an der Stelle x=1 ganz normal. Die zweite Nennernullstelle in diesem Beispiel befindet sich an der Stelle x=-1 und kürzt sich nicht weg. Hier liegt eine Polstelle vor. Polstellen treten auf, wenn der Zähler an den Nullstellen des Nenners nicht null wird. Der Funktionsgraph hat an der Stelle x=-1 eine Lücke. Es existiert an der Stelle die senkrechte Asymptote x=-1. Die Funktionswerte f(x) streben für x gegen -1 gegen plus oder minus Unendlich. Auch das Verhalten gebrochenrationaler Funktionen für x gegen Unendlich ist durch Asymptoten bestimmt. Bei echt gebrochenrationalen Funktionen, deren Zähler kleiner als der Nennergrad ist, ist immer die x-Achse eine waagerechte Asymptote, da für große x der Nenner stärker ansteigt und somit die Funktionswerte gegen Null streben. Beispiel: Die echt gebrochenrationale Funktion f mit der Funktionsgleichung f(x) = (x + 1)/(x2 + 2) strebt gegen null für x gegen plus/minus Unendlich. Der Graph hat die x-Achse als waagerechte Asymptote. Unecht gebrochenrationale Funktionen mit Grad von z größer gleich dem Grad von n können wir durch Polynomdivision in die Summe aus einem Polynom und einem echt gebrochenrationalem Funktionsterm umformen. Beispiel: Die Funktion f mit der Funktionsgleichung f(x) = (2x2 - 3x)/(x - 2) formen wir durch Anwendung der Polynomdivision in f(x) = 2x + 1 + 2/(x - 2) um. Nun wird das asymptotische Verhalten durch das Polynom bestimmt, weil ja der hintere Teil gegen null geht. Das Polynom ist die Asymptote, die nun den Beinamen “schief” bekommt. Der Graph besitzt eine schiefe Asymptote mit der Gleichung y = 2x + 1. Also eine Gerade. Damit hast du sehr wichtige Eigenschaften gebrochenrationaler Funktionen kennengelernt. Fassen wir zusammen: “Die Nullstellen eines Nenners eine gebrochenrationalen Funktion sind ihre Definitionslücken”. Es gibt “hebbare Definitionslücken” und “Polstellen”. Zudem haben wir verschiedene Arten von Asymptoten kennen gelernt. “Senkrechte Asymptoten” begegnen uns an “Polstellen”. “Waagerechte Asymptoten”, wenn der Zählergrad kleiner/gleich dem Nennergrad ist und “schiefe Asymptoten”, wenn der Zählergrad größer ist als der Nennergrad.
Gebrochenrationale Funktionen – Eigenschaften Übung
-
Beschreibe, was gebrochenrationale Funktionen sind.
TippsStellt ein Bruch ein Produkt oder einen Quotienten dar?
Die allgemeine Form ganzrationaler Funktionen lautet:
$a_0 +a_1 x^2 + ... + a_n x^n $.
Verwendet man das Zähler- oder das Nennerpolynom zur Berechnung der Nullstellen einer Funktion? Denk dir ein Beispiel für gebrochenrationale Funktionen aus und berechne die Nullstellen deiner Funktion. Was fällt dir auf?
LösungEine gebrochenrationale Funktion setzt sich aus Polynomen, genauer gesagt aus einem Zählerpolynom und einem Nennerpolynom, zusammen, welche jeweils ganzrationale Funktionen sind.
Berechnen wir die Nullstellen einer gebrochenrationalen Funktion, so setzen wir lediglich das Zählerpolynom $z(x)$ gleich Null, da stets:
$\begin{align*} f(x) &= 0 \\ 0 &= \frac{z(x)}{n(x)} &|& \cdot n(x) \\ 0 &= z(x) \end{align*}$.
Mithilfe des Nennerpolynoms $n(x)$ können wir das Verhalten der Funktion, z. B. deren Definitionslücken, bestimmen.
-
Gib die Eigenschaften der Funktionen an.
TippsDurch welche Zahl kann man niemals teilen?
Die Nullstellen des Nenners sind die Definitionslücken der Funktion. Berechne sie jeweils.
Haben das Zähler- und Nennerpolynom dieselbe Nullstelle, so nennt man sie hebbare Definitionslücke, andernfalls Polstelle.
LösungDie Nullstellen des Nenners einer gebrochenrationalen Funktion sind die Definitionslücken der Funktion.
Wir setzen also den Nenner der Funktion
$f(x)=\frac{3x^2-7x+1}{x^2+5}$
gleich Null und berechnen die möglichen Nullstellen:
$ \begin{align*} x^2+5&= 0 &|& -5 \\ x^2 &= -5 \end{align*} $
Man kann nicht die Wurzel aus negativen Zahlen ziehen, daher hat diese Funktion keine Definitionslücken im Gegensatz zu
$f(x)=\frac{x^3+2x-5}{x-3}$
mit der Definitionslücke $x=3$.
Nun betrachten wir die Funktion
$f(x)=\frac{x-1}{x^2-1}$.
Wir berechnen wieder die Nullstellen des Nenners und erhalten zwei Lösungen $x_1=1$ und $x_2=-1$. Wenn der Zähler ebenfalls dieselbe Nullstelle besitzt, so nennt man die Stelle eine hebbare Definitionslücke. Dies ist für $x_1=1$ der Fall. Andernfalls nennt man die Definitionslücke, wie $x_2=-1$, Polstelle.
-
Untersuche die Funktion auf Polstellen, hebbare Definitionslücken und Asymptoten.
TippsDie Nullstellen des Nennerpolynoms sind Definitionslücken der Funktion.
Eine hebbare Definitionslücke liegt vor, wenn der Zähler und der Nenner dieselbe Nullstelle haben.
Senkrechte Asymptoten liegen an Polstellen vor.
Du kannst die binomischen Formeln zum Umformen der Funktion anwenden.
LösungWir bestimmen als Erstes die Nullstellen des Nennerpolynoms:
$x\cdot (x-2) = 0 \qquad \Leftrightarrow \qquad x_{n_1}= 0~,~~x_{n_2}=2$.
Nun prüfen wir, ob der Zähler ebenfalls eine Nullstelle bei $0$ oder $2$ hat:
$x^2-4=0 \qquad \Leftrightarrow \qquad x_{z_1}= 2~,~~ x_{z_2}=-2$.
Da beide Polynome die Nullstelle $2$ besitzen, ist dies eine hebbare Definitionslücke und somit $x_{n_1}= 0$ eine Polstelle mit einer senkrechten Asymptote bei $x=0$.
Durch Umformung der Funktion $f(x)$ (oder durch eine Polynomdivision) können wir dies ebenfalls feststellen:
$f(x)=\frac{x^2-4}{x\cdot (x-2)}=\frac{(x+2)\cdot (x-2)}{x\cdot (x-2)}= \frac{(x+2)}{x} = 1 + \frac{2}{x}$
Außerdem erkennen wir nun, dass für $a(x)=1$ die Funktion eine waagerechte Asymptote hat.
-
Bestimme mithilfe von Polynomdivision die Asymptoten der Funktionen.
TippsDer Grad des Zählers kann kleiner, größer oder auch gleich dem Grad des Nenners sein.
Es gibt echt gebrochenrationale und unecht gebrochenrationale Funktionen. Was trifft auf diese Aufgabe zu?
Man erhält die Gleichung der schiefen Asymptote mithilfe der Polynomdivision. Bedenke, dass du den Restterm in deiner Lösung außer Acht lassen kannst.
Senkrechte Asymptoten existieren stets an Polstellen.
LösungDer Zähler der Funktion
$f(x)=\frac{x^2+6x+12}{x+3}$
hat den Grad $2$, der Nenner den Grad $1$, somit ist $f(x)$ eine unecht gebrochenrationale Funktion und besitzt eine schiefe Asymptote.
Die Gleichung der schiefen Asymptote berechnen wir mithilfe der Polynomdivision:
$(x^2+6x+12): (x+3)=x+3+\frac{3}{x+3}$.
Den Restterm können wir außer Acht lassen (da er gegen Null geht) und erhalten somit als schiefe Asymptote die Gerade
$y=x+3$.
Senkrechte Asymptoten sind stets an Polstellen vorhanden.
Da $x = -3$ nur eine Nullstelle des Nenners und nicht des Zählers ist, hat die Funktion an dieser Stelle eine senkrechte Asymptote.
-
Gib an, welche Aussagen zu den Asymptoten gebrochenrationaler Funktionen wahr sind.
TippsEine Asymptote beschreibt eine Gerade, der sich eine Funktion im Unendlichen annähert.
Eine Nullstelle, die man kürzen kann, nennt man hebbare Definitionslücke. Die Funktion und ihr Graph verhalten sich an dieser Stelle ganz normal.
Wenn Grad des Zählerpolynoms größer als der Grad des Nennerpolynoms ist, kann man eine Polynomdivision durchführen. Das Ergebnis stellt eine lineare Funktion und einen Restterm dar.
LösungUm die Definitionslücken einer gebrochenrationalen Funktion zu bestimmen, berechnet man die Nullstellen des Nenners der Funktion, da dieser nicht Null werden darf. Man unterscheidet dabei zwischen hebbaren Definitionslücken und Polstellen. Hebbar sind solche, die man durch Termumformungen kürzen kann. Dies ist der Fall, wenn der Zähler die gleiche Nullstelle besitzt wie der Nenner. Sollte dies nicht der Fall sein, so spricht man von Polstellen. An einer Polstelle hat die Funktion dann stets eine senkrechte Asymptote.
Handelt es sich bei der Funktion um eine echt gebrochenrationale Funktion, so ist der Zählergrad kleiner als der Nennergrad und die Funktion besitzt eine waagerechte Asymptote. Untersucht man eine unecht gebrochenrationale Funktion, deren Zählergrad größer oder gleich dem Nennergrad ist, so erhält man durch Polynomdivision eine lineare Funktion und einen Restterm. Die Gerade der linearen Funktion stellt eine schiefe Asymptote der gebrochenrationalen Funktion dar.
-
Ermittle die Polstellen, die hebbaren Definitionslücken sowie die Asymptoten und die Nullstellen der gegebenen Funktion.
TippsEine hebbare Definitionslücke liegt vor, wenn der Zähler und der Nenner dieselbe Nullstelle haben.
Senkrechte Asymptoten liegen an Polstellen vor.
Schiefe Asymptoten erhältst du mithilfe der Polynomdivision. Dividiere das Zählerpolynom durch das Nennerpolynom.
Setze das Zählerpolynom gleich Null, um die Nullstellen der Funktion zu berechnen.
LösungWir formen als erstes die Funktion um, indem wir ein $x$ ausklammern und anschließend kürzen:
$f(x)=\frac{x^3+2x^2-3x}{x^2+5x}= \frac{x(x^2+2x-3)}{x(x+5)} = \frac{x^2+2x-3}{x+5}$.
Da wir die Nullstelle $x = 0$ des Nenners kürzen konnten, liegt an dieser Stelle eine hebbare Definitionslücke vor. Lediglich $x = -5$ ist eine Polstelle der Funktion und somit auch eine senkrechte Asymptote.
Um die schiefe Asymptote zu berechnen, dividieren wir das Zählerpolynom durch das Nennerpolynom und erhalten:
$(x^2+2x-3) : (x+5)=x-3+\frac{12}{x+5}$.
$y=x-3$ ist also unsere schiefe Asymptote, welche die Form einer Geraden hat.
Als letztes berechnen wir noch die Nullstellen der Funktion, indem wir $f(x) = 0$ setzen. Bei gebrochenrationalen Funktionen kann man die Berechnung der Nullstellen abkürzen, indem man gleich das Zählerpolynom mit Null gleichsetzt und die Nullstellen berechnet.
Wir verwenden dafür die p-q-Formel:
$\begin{align*} x_{1,2} &= -\frac{2}{2}\pm \sqrt{(\frac{2}{2})^2-(-3)} \\ x_1 &=-1+2=1 \\ x_2 &=-1-2=-3 \end{align*}$.
Da $x_1=1$ und $x_2=-3$ im Definitionsbereich enthalten sind, sind dies die Nullstellen der Funktion.
10.798
Lernvideos
44.117
Übungen
38.764
Arbeitsblätter
24h
Hilfe von Lehrer/
-innen
Inhalte für alle Fächer und Klassenstufen.
Von Expert/-innen erstellt und angepasst an die Lehrpläne der Bundesländer.
6 Kommentare
Für was sind eigentlich gebrochenrationale Funktionen gut
Das Video ist super hilfreich gewesen. Man sieht, wie viel Mühe sich gegeben wurde.
@Bethwagner:
Der Grenzwert ist für limes x gegen 1 von 1/x+1=
1/ 1+1=1/2
Wenn man x gegen Unendlich oder Minus Unendlich laufen lässt, dann ist der Grenzwert jeweils 0, da der Nenner dann unendlich groß wird. Für x gegen 1 existiert der Grenzwert allerdings mit 1/2, da ich x ohne Probleme für 1 ersetzen kann.
Ich hoffe, dass ich helfen konnte.
Ich meine bei 4:01
Bei 4:10 ist der Grenzwert doch 0 !!??