Gebrochenrationale Funktionen – Definitionslücken und Asymptoten


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Gebrochenrationale Funktionen – Definitionslücken und Asymptoten
Zunächst lernst du, was der Unterschied zwischen einer “hebbaren Definitionslücke” und einer “Polstelle” ist. Anschließend erfährst du, wann eine gebrochenrationale Funktion eine waagerechte, senkrechte beziehungsweise schräge Asymptote hat.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Definitionslücke, hebbare Definitionslücke, Polstelle und Asymptote.
Bevor du dieses Video schaust, solltest du bereits grundlegendes Wissen zu gebrochenrationalen Funktionen haben.
Transkript Gebrochenrationale Funktionen – Definitionslücken und Asymptoten
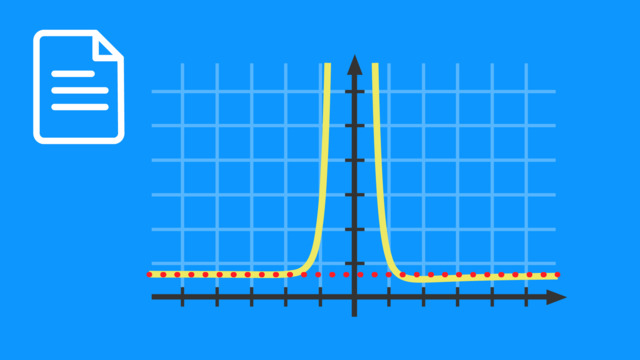
Ob du es glaubst oder nicht, auch Funktionen sind von Zeit zu Zeit einsam. So wie dieser kleine Fratz hier! Sie sehnen sich dann nach einer wärmenden Asymptote, an die sie sich anschmiegen können. Wie das Ganze bei "gebrochenrationalen Funktionen" aussehen kann und was wir dabei zu beachten haben, klären wir in diesem Video. Wir gehen also der Frage auf den Grund, was es mit "Definitionslücken" und "Asymptoten" von gebrochenrationalen Funktionen auf sich hat. Tatsächlich kann man auch bei diesen beiden Begriffen nochmal unterscheiden. Definitionslücken können sogenannte "hebbare" Definitionslücken, oder aber auch "Polstellen" sein. Und auch bei Asymptoten unterscheiden wir noch zwischen verschiedenen Typen. Da gibt es nämlich einmal waagerechte und senkrechte, aber zum Beispiel auch schräge Asymptoten. Keine Sorge! Nach diesem Video wird das Ganze deutlich klarer sein. Wir beginnen mit den Definitionslücken. Das sind ja Stellen beziehungsweise x-Werte, für die eine bestimmte Funktion gar nicht definiert ist. In anderen Worten: Es sind Lücken in der Definitionsmenge all der x-Werte, für die die Funktion einen Funktionswert annimmt. Diese Lücken ergeben sich bei gebrochenrationalen Funktionen immer dann, wenn der NENNER des Funktionsterms gleich Null wäre. Denn in diesem Fall würden wir durch Null teilen, was wiederum eben mathematisch nicht definiert ist. Doch warum unterscheiden wir jetzt noch zwischen VERSCHIEDENEN Definitionslücken: "hebbaren Definitionslücken" und "Polstellen"? Die Funktionen sind an diesen Stellen doch eh nicht definiert. Das liegt daran, dass das VERHALTEN der Funktion um die Nullstellen herum sehr unterschiedlich sein kann. Deutlich wird das an DIESER gebrochenrationalen Funktion. Da der Nenner hier in "faktorisierter Form" vorliegt, können wir dessen Nullstellen einfach ablesen. An DIESEN Nullstellen des Nenners hat die Funktion also Definitionslücken, das ist schonmal klar. Aber EINE dieser Definitionslücken unterscheidet sich von den anderen beiden. Das erkennen wir, wenn wir uns den Funktionsgraphen der Funktion anschauen. Wir schauen zunächst auf die Stelle "x gleich minus drei". Erstmal fällt an dieser Stelle keine Besonderheit auf. Der Funktionsgraph sieht hier ganz normal aus. Das liegt aber nur daran, dass die Definitionslücke an dieser Stelle UNENDLICH klein ist. Normalerweise wird eine solche Definitionslücke mit einem kleinen Kringel symbolisiert. Da sie aber eigentlich so klein ist, dass man sie gar nicht erkennen kann und die Funktion in der Nähe dieser Lücke keine großen Sprünge macht (man sagt auch "sie ist an dieser Stelle "stetig fortsetzbar""), sprechen wir in diesem Fall von einer "hebbaren Definitionslücke", also einer Definitionslücke, die gewissermaßen "überbrückbar" ist. "Hebbare Definitionslücken" kommen bei gebrochenrationalen Funktionen immer dann zustande, wenn eine Nullstelle des Nenners gleichzeitig auch eine Nullstelle des Zählers ist und sich die Nullstelle kürzen lassen würde. "x gleich minus drei" ist in unserem Fall auch eine Nullstelle des Zählers, wie durch eine Faktorisierung schnell ersichtlich wird. Damit liegt an dieser Stelle also eine "hebbare Definitionslücke" vor, denn jetzt sehen wir, dass wir DIESE Nullstelle kürzen könnten. Wenn wir das tun, ändern wir die Funktion aber(!) – beziehungsweise erschaffen streng genommen eine neue Funktion. Der entsprechende Funktionsgraph der GEKÜRZTEN Funktion "g von x" verläuft dann praktisch genauso, nur dass er eben an der Stelle "x gleich minus drei" KEINE Definitionslücke hat. Anders sieht es bei den Definitionslücken "x-eins gleich drei" und "x-zwei gleich eins" aus. Hier erkennen wir relativ deutlich, dass die Funktion an diesen Stellen keinen Funktionswert annimmt. Noch deutlicher wird das, wenn wir jeweils eine senkrechte Gerade bei "x-zwei gleich eins" und "x-eins gleich drei" einzeichnen. Der Funktionsgraph nähert sich diesen Geraden an mehreren Stellen immer weiter an, ohne sie jemals zu erreichen, da die Funktion für diese Stellen ja nicht definiert ist. Wir nennen diese Geraden daher auch "Asymptoten" der Funktion "f von x". Eine "Asymptote" ist also eine Kurve (meistens in Form einer Geraden), der sich eine Funktion immer weiter annähert. Definitionslücken einer Funktion, die sich durch solche senkrechten Asymptoten auszeichnen, nennen wir "Polstellen". Die Funktionswerte der Funktion gehen für x-Werte, die sich der "Polstelle" immer weiter annähern, gegen "plus unendlich" beziehungsweise "minus unendlich". Bei unserem Funktionsgraphen haben wir dabei jeweils einen Vorzeichenwechsel. Einmal von "minus unendlich" zu "plus unendlich" und einmal von "plus unendlich zu "minus unendlich". Denkbar sind aber natürlich auch Polstellen ohne Vorzeichenwechsel, die dann zum Beispiel SO beziehungsweise SO aussehen könnten. Alles klar, dann haben wir "Definitionslücken" schonmal abgehakt. Und was eine "Asymptote" ist, wissen wir jetzt auch schon. SENKRECHTE Asymptoten treten bei einer gebrochenrationalen Funktion immer dann auf, wenn sie Polstellen hat, also "nicht hebbare Definitionslücken". Es gibt allerdings noch weitere Asymptoten, die untersucht werden können. Hier sind zunächst die WAAGERECHTEN Asymptoten zu nennen. Häufig ist die X-ACHSE eine waagerechte Asymptote – wie auch bei unserer Funktion. Das ist immer dann der Fall, wenn der Grad der ZÄHLERfunktion (in unserem Fall gleich zwei) kleiner als der Grad der NENNERfunktion ist (in unserem Fall gleich drei). Wenn wir x gegen "minus unendlich" laufen lassen, nähert sich der Funktionsgraph der x-Achse von unten. Für x gegen "plus unendlich" nähert er sich von oben. Wir können am Beispiel dieser Funktion dann auch mit einem Vorurteil gegenüber Asymptoten aufräumen: Es stimmt nicht, dass der Graph die Asymptote definitiv nie berührt beziehungsweise schneidet. Wie wir hier sehen, schneidet der Funktionsgraph die x-Achse bei "x gleich fünf". In den äußeren Bereichen des Funktionsgraphen können wir aber das typische asymptotische Verhalten beobachten. Hier gilt tatsächlich, dass der Graph die x-Achse nicht mehr schneidet, sondern sich immer weiter an sie anschmiegt, ohne sie zu berühren. Eine waagerechte Asymptote, die NICHT genau auf der x-Achse liegt, haben wir gegeben, wenn der Zählergrad einer gebrochenrationalen Funktion GLEICH ihrem Nennergrad ist. Für diesen Fall schauen wir uns eine Funktion an, die das Kriterium erfüllt. Hier können wir die Gleichung der entsprechenden Gerade bestimmen, indem wir die Vorfaktoren der beiden Terme mit der höchsten x-Potenz dividieren. Für diese Funktion haben wir also eine Asymptote bei "y gleich zwei". Was sich bestätigt, wenn wir den Graphen der Asymptote dazu einzeichnen. Diese Asymptote verläuft dann also parallel zur x-Achse Ein letzter Fall noch, dann haben wir es geschafft! Der Grad der Zählerfunktion kann natürlich auch größer sein, als der der Nennerfunktion. In diesem Fall haben wir entweder eine schräge Asymptote (das ist immer DANN so, wenn der Zählergrad genau um eins höher ist als der Nennergrad, wie bei DIESER Funktion hier) oder sogar eine gekrümmte Asymptote (sprich eine Kurve), wenn die Differenz zwischen Zähler- und Nennergrad noch größer ist. Auch diese Asymptoten lassen sich bestimmen, hierzu braucht es dann aber schon die Polynomdivision. Wir machen an dieser Stelle aber einen Cut und schauen uns die wichtigsten Infos nochmal auf einen Blick an. Wir haben uns in diesem Video mit Definitionslücken und Asymptoten von gebrochenrationalen Funktionen beschäftigt. Definitionslücken können entweder "hebbare Definitionslücken" sein (das ist der Fall, wenn wir die entsprechende Nullstelle des Nenners aus dem Funktionsterm kürzen könnten) oder es handelt sich um "Polstellen". "Polstellen" kommen also durch Nullstellen der Nennerfunktion zustande, die NICHT gekürzt werden können und zeichnen sich durch eine senkrechte Asymptote aus. Waagerechte Asymptoten sind immer dann vorhanden, wenn der Zählergrad kleiner als oder gleich dem Nennergrad ist. Und eine schräge oder kurvenförmige Asymptote liegt vor, wenn der Zählergrad größer als der Nennergrad ist. Es gibt also verschiedenste Asymptoten, an die sich so eine gebrochenrationale Funktion schmiegen kann, wobei diese Asymptoten in vielen Fällen nie erreicht werden. Ganz so eng nehmen es die Pinguine aber zum Glück nicht. Da darf auch mit Körpereinsatz fleißig gekuschelt werden.
Gebrochenrationale Funktionen – Definitionslücken und Asymptoten Übung
-
Entscheide, um welche Art von Definitionslücke es sich handelt.
TippsHier siehst du den Funktionsgraphen der Funktion $f(x)$.
- Hebbare Definitionslücke: Die entsprechende Nullstelle des Nenners ist auch eine Nullstelle des Zählers. Sie würde sich also kürzen lassen.
- Polstelle: Polstellen sind nicht hebbare Definitionslücken. Die Nullstelle des Nenners ist hier also keine Nullstelle des Zählers.
LösungDefinitionslücken einer Funktion sind $x$-Werte, für die die Funktion nicht definiert ist: Sie nimmt für den $x$-Wert keinen Funktionswert an.
Bei gebrochenrationalen Funktionen kann man die Definitionslücken mit den Nullstellen des Nenners identifizieren. Der Grund liegt darin, dass man nicht durch null teilen darf: Diese Operation ist nicht definiert. Der Nenner darf also nicht den Wert null annehmen.Wir unterscheiden zwischen:
- hebbaren Definitionslücken und
- Polstellen.
Hebbare Definitionslücke:
Die entsprechende Nullstelle des Nenners ist auch eine Nullstelle des Zählers. Sie würde sich also kürzen lassen.
Am Funktionsgraphen ist eine hebbare Definitionslücke nur durch einen kleinen Kringel darstellbar, der Graph verläuft ansonsten normal und macht keine Sprünge.Polstelle:
Polstellen sind nicht hebbare Definitionslücken. Die Nullstelle des Nenners ist hier also keine Nullstelle des Zählers.
Der Funktionsgraph nähert sich an diesen Stellen an senkrechte Asymptoten an.Wir betrachten nun die gegebene Funktion:
$f(x) = \dfrac{(x+3)(x-5)}{(x-3)(x-1)(x+3)}$
Wir können die Nullstellen des Nenners direkt ablesen:
$x_1=3 \quad x_2=1 \quad x_3=-3$
- $x=5$ ist keine Nullstelle des Nenners, sondern nur eine Nullstelle des Zählers. Es handelt sich daher hierbei um keine Definitionslücke. Die Stelle weist auch im Funktionsgraphen keine Auffälligkeiten auf.
- $x=-3$ ist sowohl Nullstelle des Nenners als auch Nullstelle des Zählers. Es handelt sich also hierbei um eine hebbare Definitionslücke. Sie ist im Funktionsgraphen lediglich durch einen kleinen Kringel symbolisiert.
- $x=1$ ist nur eine Nullstelle des Nenners und somit eine Polstelle. Der Funktionsgraph macht hier einen Vorzeichenwechsel $- \rightarrow +$.
- $x=3$ ist ebenfalls nur eine Nullstelle des Nenners und somit eine Polstelle. Der Funktionsgraph macht hier einen Vorzeichenwechsel $+ \rightarrow -$.
-
Gib an, welche Aussagen zu Asymptoten richtig sind.
TippsEine Asymptote ist eine Kurve beziehungsweise meistens eine Gerade, an die sich eine Funktion immer weiter annähert.
Wir unterscheiden zwischen:
- senkrechten Asymptoten
- waagerechten Asymptoten
- schrägen Asymptoten
- kurvenförmigen Asymptoten
Es sind drei Aussagen richtig.
LösungEine Asymptote ist eine Kurve beziehungsweise meistens eine Gerade, an die sich eine Funktion immer weiter annähert.
Wir unterscheiden zwischen:
- senkrechten Asymptoten: Diese treten bei Polstellen auf.
- waagerechten Asymptoten: Diese treten immer dann auf, wenn der Grad des Zählerpolynoms kleiner oder gleich dem Grad des Nennerpolynoms ist. Häufig ist die $x$-Achse eine waagerechte Asymptote.
- schräge oder kurvenförmige Asymptoten: Diese liegen vor, wenn der Grad des Zählerpolynoms größer als der Grad des Nennerpolynoms ist.
Wir überprüfen damit die Aussagen:
- Asymptoten sind immer senkrechte Geraden, an die sich der Funktionsgraph immer weiter annähert.
- Wenn der Grad des Zählerpolynoms kleiner ist als der Grad des Nennerpolynoms, dann treten waagerechte Asymptoten auf.
- Es gibt auch kurvenförmige Asymptoten.
- An einer Polstelle nähert sich der Funktionsgraph immer einer senkrechten Asymptote an.
-
Beschreibe das Verhalten der gebrochenrationalen Funktion.
TippsDu kannst im Nenner ein $x$ ausklammern und erhältst:
$\dfrac{3x}{x(x+1)(x-2)^2}$
Eine hebbare Definitionslücke ist gleichzeitig Nullstelle der Zählerfunktion und der Nennerfunktion.
LösungWir betrachten die gegebene Funktionsgleichung:
$\dfrac{3x}{(x^2+x)(x-2)^2}$
Zunächst fällt auf, dass wir im Nenner ein $x$ ausklammern können, um die Nullstellen vom Nenner besser erkennen und mit dem Zähler vergleichen zu können:
$\dfrac{3x}{x(x+1)(x-2)^2}$
Wir sehen nun, dass $x=0$ eine Nullstelle des Nenners und gleichzeitig Nullstelle des Zählers ist. Es handelt sich hierbei somit um eine hebbare Definitionslücke.
Außerdem weist der Nenner noch die Nullstelle $x=-1$ auf. Hierbei handelt es sich um keine Nullstelle der Zählerfunktion – es ist also eine Polstelle. Auch $x=2$ ist eine Nullstelle des Nenners, aber keine Nullstelle des Zählers und deshalb eine Polstelle. Da es keine weiteren Nullstellen in der Nennerfunktion gibt, können wir festhalten, dass die Funktion genau zwei Polstellen hat. An diesen beiden Polstellen hat die Funktion senkrechte Asymptoten, also hat sie zwei senkrechte Asymptoten.
Wir betrachten jetzt weitere Asymptoten. Dazu untersuchen wir den Grad des Zählers und des Nenners. Der Grad des Zählers ist $1$, denn $3x = 3x^1$. Der Grad des Nenners ist $4$. Das erkennen wir, weil beim Ausmultiplizieren aller Klammern der erste Summand $x^4$ wäre. Der Grad der Zählerfunktion ist also kleiner als der Grad der Nennerfunktion. Somit hat der Funktionsgraph eine waagerechte Asymptote. Dies ist in unserem Fall die $x$-Achse. Wir schreiben für das Verhalten im Unendlichen:
$ \lim \limits_{x \to + \infty} f(x) = 0$ und $ \lim \limits_{x \to - \infty} f(x) = 0$
-
Untersuche die Funktion auf Definitionslücken und Asymptoten.
TippsDie Nullstellen der Nennerfunktion sind $x_1=-3$ und $x_2=+3$.
Die Geradengleichung der $x$-Achse ist $y=0$.
Hier kannst du den Graphen $f$ sehen.
LösungWir betrachten die gegebene Funktion:
$f(x) = \dfrac{3x}{x^2-9}$
Zunächst bestimmen wir die Nullstellen des Nenners:
$\begin{array}{llll} x^2-9 & = & 0& |+9 \\ x^2 & = & 9 & | \pm \sqrt{} \\ x & = & \pm 3 & \end{array}$
Wir erhalten also die Nullstellen der Nennerfunktion:
$x_1=-3$ und ${x_2=+3}$
Da es sich hierbei um keine Nullstellen des Zählers handelt, sind beides Polstellen. Somit hat die Funktion die senkrechten Asymptoten $x=-3$ und ${x=+3}$. Bei ${x=-3}$ macht die Funktion einen Vorzeichenwechsel von $-$ nach $+$, bei $x=+3$ macht die Funktion einen Vorzeichenwechsel von $+$ nach $-$. Dies können wir am Funktionsgraphen erkennen oder durch Einsetzen von Werten, welche etwas größer und etwas kleiner als der gegebene Wert sind.
Außerdem können wir erkennen, dass der Grad der Zählerfunktion kleiner als der Grad der Nennerfunktion ist. Somit hat die Funktion eine waagerechte Asymptote – nämlich die $x$-Achse. Wir schreiben sie als $y=0$.
-
Bestimme, ob der abgebildete Funktionsgraph Polstellen hat.
TippsWir erkennen Polstellen im Funktionsgraphen daran, dass sich der Graph an diesen Stellen einer senkrechten Asymptote annähert.
Dieser Funktionsgraph hat eine Polstelle.
Drei der abgebildeten Graphen haben eine Polstelle.
LösungAn einer Polstelle hat eine Funktion eine Definitionslücke – die Funktion nimmt hier keinen Funktionswert an. Wir erkennen Polstellen im Funktionsgraphen daran, dass sich der Graph an diesen Stellen einer senkrechten Asymptote annähert.
Eine Asymptote ist eine Kurve beziehungsweise meistens eine Gerade, an die sich eine Funktion immer weiter annähert.
Wir betrachten die Funktionsgraphen:
1. Graph: blaue Potenzfunktion
$\Rightarrow$ Dieser Funktionsgraph weist keine Polstelle auf.2. Graph: grüne Hyperbel
$\Rightarrow$ Dieser Funktionsgraph hat eine Polstelle bei $x=0$. Die $y$-Achse ist also in diesem Fall die Asymptote.3. Graph: orange Hyperbel
Dieser Funktionsgraph hat eine Polstelle bei $x=2$. Die Asymptote ist gestrichelt eingezeichnet.4. Graph: grüne Parabel
Dieser Funktionsgraph weist keine Polstelle auf.5. Graph: lila Potenzfunktion
Dieser Funktionsgraph weist ebenfalls keine Polstelle auf.6. Graph: orange Hyperbel
Dieser Funktionsgraph hat eine Polstelle bei $x=0$. Die $y$-Achse ist also auch in diesem Fall die Asymptote. -
Vervollständige den Funktionsgraphen jeweils so, dass die geforderte Eigenschaft erfüllt ist.
TippsWir unterscheiden zwischen den folgenden Asymptoten:
- senkrechte Asymptoten: Sie treten bei Polstellen auf.
- waagerechte Asymptoten: Sie treten immer dann auf, wenn der Grad der Zählerfunktion kleiner oder gleich dem Grad der Nennerfunktion ist.
- schräge Asymptoten: Sie treten auf, wenn der Grad der Zählerfunktion um $1$ größer als der Grad der Nennerfunktion ist.
- kurvenförmige Asymptoten: Sie treten auf, wenn der Grad der Zählerfunktion um mehr als $1$ größer als der Grad der Nennerfunktion ist.
Bei der ersten Funktion hilft es, im Zähler ein $x$ auszuklammern:
$x^2-ax = x(x-a)$
LösungDefinitionslücken einer Funktion sind $x$-Werte, für die die Funktion nicht definiert ist: Sie nehmen für diese $x$-Werte keinen Funktionswert an.
Wir unterscheiden zwischen:
- hebbaren Definitionslücken: Diese sind Nullstellen der Nennerfunktion und der Zählerfunktion.
- Polstellen: Sie sind nur Nullstellen der Nennerfunktion.
Eine Asymptote ist eine Kurve beziehungsweise meistens eine Gerade, an die sich eine Funktion immer weiter annähert.
Wir unterscheiden:
- senkrechte Asymptoten: Sie treten bei Polstellen auf.
- waagerechte Asymptoten: Sie treten immer dann auf, wenn der Grad der Zählerfunktion kleiner oder gleich dem Grad der Nennerfunktion ist.
- schräge Asymptoten: Sie treten auf, wenn der Grad der Zählerfunktion um $1$ größer als der Grad der Nennerfunktion ist.
- kurvenförmige Asymptoten: Sie treten auf, wenn der Grad der Zählerfunktion um mehr als $1$ größer als der Grad der Nennerfunktion ist.
Wir betrachten mit diesem Wissen die gegebenen Funktionen:
Erste Funktion: $f(x)= \dfrac{x^2-ax}{(x-3)(x-4)(x+3)}$
Sie soll eine hebbare Definitionslücke bei $x=-3$ haben. Dazu muss dies eine Nullstelle der Nennerfunktion und der Zählerfunktion sein. Im Nenner können wir die Nullstelle an dem Faktor $(x+3)$ erkennen. Im Zähler können wir ein $x$ ausklammern:
$x^2-ax = x(x-a)$
Also muss die Variable $a=-3$ sein, damit die Funktion bei $x=-3$ eine Zählernullstelle und somit eine hebbare Definitionslücke hat.
Zweite Funktion: $g(x)= \dfrac{x^a}{x^3-2}$
Sie soll eine schräge Asymptote haben. Dazu muss der Grad der Zählerfunktion um $1$ größer als der Grad der Nennerfunktion sein. Da der Grad $3$ ist, muss der Grad der Zählerfunktion $a=4$ sein.
Dritte Funktion: $h(x)= \dfrac{x}{x^2-a}$
Sie soll eine Polstelle bei $x=2$ haben. Dazu muss $x=2$ Nullstelle des Nenners sein (und keine Nullstelle des Zählers, was gegeben ist). Wir setzen also $2^2-a=0$ und erhalten durch Auflösen der Gleichung die Variable $a=4$.
9.718
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.275
Lernvideos
38.579
Übungen
33.616
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?