Gauß-Verfahren
Das Gauß-Verfahren, auch Gauß-Algorithmus genannt, ist ein Verfahren zur Bestimmung linearer Gleichungssysteme. Im Folgenden erfährst du, wie ein lineares Gleichungssystem mithilfe des Eliminationsverfahrens gelöst werden kann.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Lineare Gleichungssysteme
- Wie kann ein solches lineares Gleichungssystem gelöst werden?
- Das Gauß'sche Eliminationsverfahren
- Beispiel
- Lösen des LGS durch Rückwärtseinsetzen
Lineare Gleichungssysteme
Ein lineares Gleichungssystem (LGS) besteht häufig aus zwei oder mehr linearen Gleichungen mit ebenso vielen Variablen. Die Variablen sind die Unbekannte, nach denen die Gleichungen gelöst werden sollen.
Hier siehst du ein Beispiel für ein LGS mit drei Gleichungen und drei Unbekannten
$\begin{array}{lrcl} (I)&5x -4y+~z &=& -3\\ (II)&2x+~y-3z &=& ~10\\ (III)&3x-~y -~z&=&~~4 \end{array}$
Es wird das Lösungstriple $(x|y|z)$ gesucht, welches die drei Gleichungen erfüllt.
Wie kann ein solches lineares Gleichungssystem gelöst werden?
Hierfür kennst du sicher noch unterschiedliche Verfahren:
- das graphische Lösen linearer Gleichungssysteme,
- das Additionsverfahren,
- das Gleichsetzungsverfahren und
- das Einsetzungsverfahren.
Bei letztgenannten drei Verfahren schreibst du immer die Gleichungen inklusive der Unbekannten auf.
Ein weiteres Verfahrens, welches auf das Additionsverfahren zurückzuführen ist, ist das Gauß'sche Eliminationsverfahren.
Das Gauß'sche Eliminationsverfahren
Das Gauß'sche Eliminationsverfahren oder auch kurz das Gauß-Verfahren oder der Gauß-Algorithmus ist ein Verfahren zur Bestimmung von Lösungen linearer Gleichungssysteme. Ziel des Verfahrens ist es, ein lineares Gleichungssystem so umzuformen, dass es eine obere Dreiecksgestalt hat.
Durch diese Form des Lösens sparst du recht viel Schreibaufwand. Du musst nicht jedes Mal die komplette Gleichung aufschreiben.
Beispiel
Zunächst wird das LGS, am Beispiel des obigen LGS, in Form einer Tabelle aufgeschrieben. Dies obigen Beispiel sieht dann so aus:
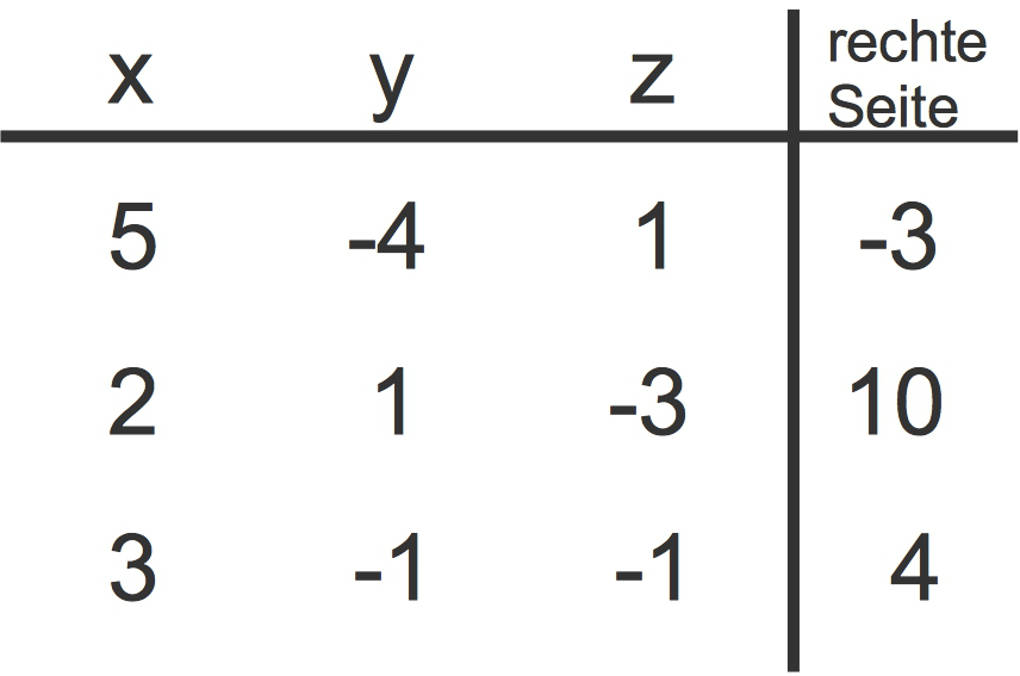
Jede Zeile in dieser Tabelle steht für eine Gleichung. Du siehst auf der jeweils rechten Seite der Tabelle die rechte Seite der Gleichung. Links stehen die Koeffizienten der Unbekannten $x$, $y$ und $z$.
Du kennst eine solche Schreibweise vielleicht vom Lösen von linearen Gleichungssystemen mit Matrizen. So ähnlich sieht die erweiterte Koeffizientenmatrix aus.
Ähnlich wie beim Additionsverfahren addierst du das Vielfache einer Zeile (Gleichung) zu dem Vielfachen einer anderen Zeile (Gleichung). Dies ist eine elementare Zeilenumformung oder Äquivalenzumformung. Sie stellen einen wesentlichen Punkt des Gauß-Algorithmus' dar. Das Aussehen des Gleichungssystems wird zwar verändert, allerdings nicht die Lösungen.
Wenn du in einem ersten Schritt das $-2$-Fache der ersten Zeile zu dem $5$-fachen der zweiten Zeile addierst, wird das erste Element in der zweiten Zeile zu $0$:
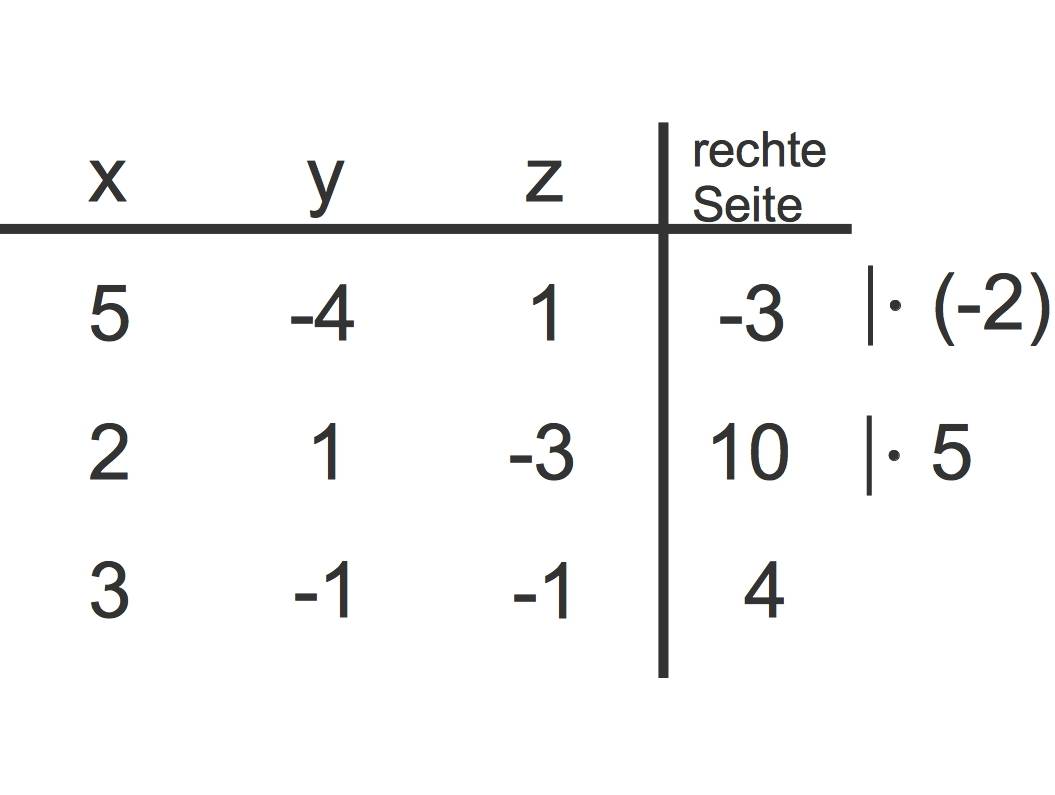
Die erste Zeile bleibt erhalten.
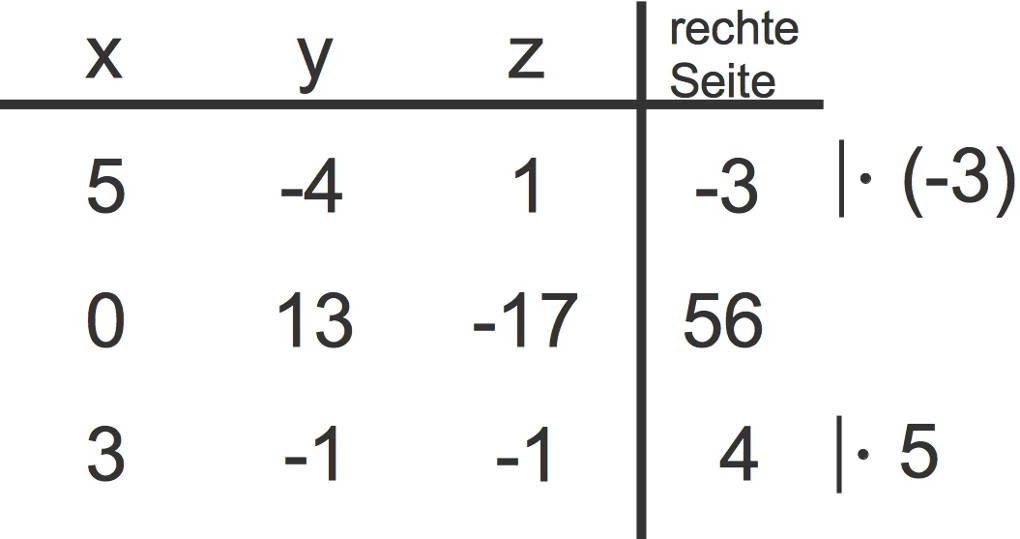
Nun addierst du das $-3$-Fache der ersten Zeile zu dem $5$-fachen der dritten Zeile. Die beiden ersten Elemente in der zweiten und dritten Zeile sind bereits $0$.
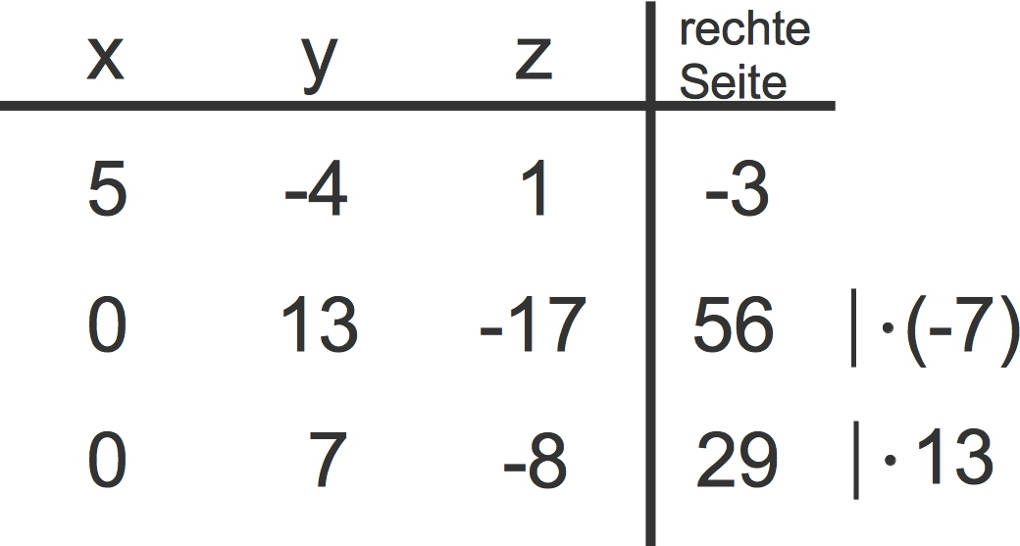
Zuletzt addierst du das $-7$-fache der zweiten Zeile zu dem $13$-fachen der dritten Zeile. Die zweite Zeile bleibt erhalten.
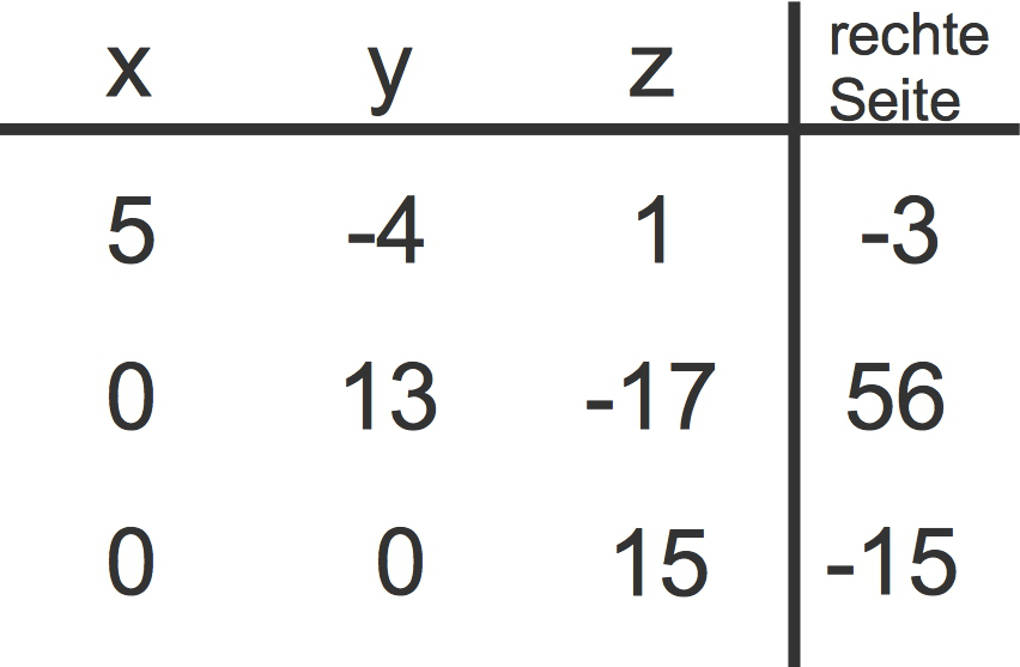
Jetzt hat das Gleichungssystem, genauer die zugehörige Tabelle, eine obere Dreiecksgestalt.
Das LGS wird jetzt durch Rückwärtseinsetzen gelöst.
Lösen des LGS durch Rückwärtseinsetzen
- Die letzte Zeile lautet $15z=-15$. Division durch $15$ führt zu $z=-1$.
- Die zweite Zeile lautet $13y-17z=56$. Hier wird der bereits bekannte Wert von $z$ eingesetzt: $13y+17=56$. Subtraktion von $17$ führt zu $13y=39$. Nun wird durch $13$ dividiert: $y=3$.
- Die erste Zeile ist die erste Gleichung des LGS. Diese Zeile bleibt erhalten. $5x-4y+z=-3$. Auch hier werden die bereits bekannten Werte für die Unbekannten eingesetzt: $5x-12-1=-3$. Addition von $13$ führt zu $5x=10$ und Division durch $5$ liefert den Wert für $x=2$.
Die gesuchte Lösung lautet $(2|3|-1)$.
Lösbarkeit von LGS
Wenn du dir bei dem obigen Beispiel die letzte Zeile bei der letzten Tabelle anschaust, kannst du die Gleichung $15z=-15$ aufschreiben. Diese liefert eine eindeutige Lösung für $z$, nämlich $z=-1$.
- Die letzte Zeile könnte aber auch so aussehen: $0\quad0\quad0\quad|\quad r$ mit $r\neq 0$. Dies würde zu der Gleichung $0=r$ führen, welche keine Lösung hat. Das bedeutet, dass das gesamte LGS unlösbar ist.
- Die letzte Zeile könnte auch so aussehen: $0\quad0\quad0\quad|\quad0$. Die zugehörige Gleichung lautet dann $0=0$, welche unendlich viele Lösungen hat. Dann hat auch das zugehörige LGS unendlich viele Lösungen.
Beispiel für unendlich viele Lösungen
$\begin{array}{lrcl} (I)&5x -~y&=& 10\\ (II)&-20x+~4y &=& ~-40\end{array}$
Dieses LGS wird hier einmal mit Matrizen gelöst:
- Zunächst wird die erweiterte Koeffizientenmatrix aufgestellt. Diese hat zwei Zeilen (Anzahl der Gleichungen) und drei Spalten (Anzahl der Unbekannten plus rechte Seite).
$\quad~~~$$\begin{pmatrix} 5&-1&|& 10 \\ -20&4&|&-40 \end{pmatrix}$
- Du kannst hier sicher die Ähnlichkeit zu der Tabelle im Gauß-Algorithmus erkennen.
- Nun wird das $4$-Fache der ersten Zeile zu der zweiten addiert und du erhältst
$\quad~~~\begin{pmatrix} 5&-1&|& 10 \\ 0&0&|&0 \end{pmatrix}$
- Die letzte Zeile ist eine Nullzeile. Die zugehörige Gleichung lautet $0=0$.
- Eigentlich besteht das LGS nur aus einer Gleichung, hat allerdings zwei Unbekannte. Du kannst eine Unbekannte frei wählen und die andere in Abhängigkeit dazu berechnen.
- Es gibt unendlich viele Lösungen des LGS
Alle Videos zum Thema
Videos zum Thema
Gauß-Verfahren (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gauß-Verfahren (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Gauß-Algorithmus – Erklärung
Gauß-Algorithmus – Erklärung
 Mit Matrizen lineare Gleichungssysteme lösen – Einführung
Mit Matrizen lineare Gleichungssysteme lösen – Einführung
 Mit Matrizen lineare Gleichungssysteme lösen – Beispiel
Mit Matrizen lineare Gleichungssysteme lösen – Beispiel









