Grundlagen zu Matrizen
Ordnung, Transportmatrix, Inzidenzmatrix, Stücklisten, Übergangsmatrix
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine Matrix?
- Spezielle Matrizen
- Quadratische Matrizen
- Diagonalmatrizen
- Die Einheitsmatrix
- Obere oder untere Dreiecksmatrix
Was ist eine Matrix?
Ein solches rechteckiges Schema
$A=\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n} \\ a_{21}&a_{22}&\dots&a_{2n} \\ \vdots&\vdots&&\vdots \\ a_{m1}&a_{m2}&\dots&a_{mn} \\ \end{pmatrix}$
heißt Matrix.
Dabei ist $m$ die Anzahl der Zeilen und $n$ die Anzahl der Spalten dieser Matrix. Entsprechend dieser Anzahlen ist die Ordnung der Matrix definiert: Die obige Matrix ist eine $[m\times n]$-Matrix.
Mit Hilfe von Matrizen können in der Mathematik Zusammenhänge dargestellt werden, zum Beispiel Veränderungen in Form von Übergangsmatrizen.
Spezielle Matrizen
Quadratische Matrizen
Matrizen, welche die gleiche Anzahl an Zeilen wie an Spalten haben, werden quadratisch genannt.
Diagonalmatrizen
$D=\begin{pmatrix} a_{11}&0&\dots&0 \\ 0&\ddots&\ddots&\vdots \\ \vdots&\ddots&\ddots&0 \\ 0&\dots&0&a_{nn} \\ \end{pmatrix}$
Bei Diagonalmatrizen sind alle Elemente außer denen auf der Hauptdiagonalen (von oben links nach unten rechts) gleich $0$.
Die Diagonale, die von unten links nach oben rechts verläuft, heißt Nebendiagonale.
Die Einheitsmatrix
Die Einheitsmatrix ist eine spezielle Diagonalmatrix. Auf der Diagonalen stehen nur Einsen:
$I=\begin{pmatrix} 1&0&\dots&0 \\ 0&\ddots&\ddots&\vdots \\ \vdots&\ddots&\ddots&0 \\ 0&\dots&0&1 \\ \end{pmatrix}$.
Bei der Matrixmultiplikation ist $I$ das neutrale Element. Eine Matrix, die mit der Einheitsmatrix multipliziert wird, ändert sich nicht.
Obere oder untere Dreiecksmatrix
Bei einer oberen Dreiecksmatrix sind alle Elemente unterhalb der Hauptdiagonalen gleich $0$:
$D=\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n} \\ 0&a_{22}&\dots&a_{2n} \\ \vdots&\ddots&\ddots&\vdots \\ 0&\dots&0&a_{nn} \\ \end{pmatrix}$.
Entsprechend sind bei einer unteren Dreiecksmatrix alle Elemente oberhalb der Hauptdiagonalen $0$.
Übergangsmatrizen
Mathematische Prozesse können mit Hilfe von Matrizen dargestellt werden.
Schaue dir das folgende Beispiel an. Die Kunden der drei Supermärkte $A$, $B$ und $C$ wechseln hin und wieder von einem Supermarkt zu einem anderen. Das Wechselverhalten der Kunden ist in diesem Übergangsdiagramm dargestellt:
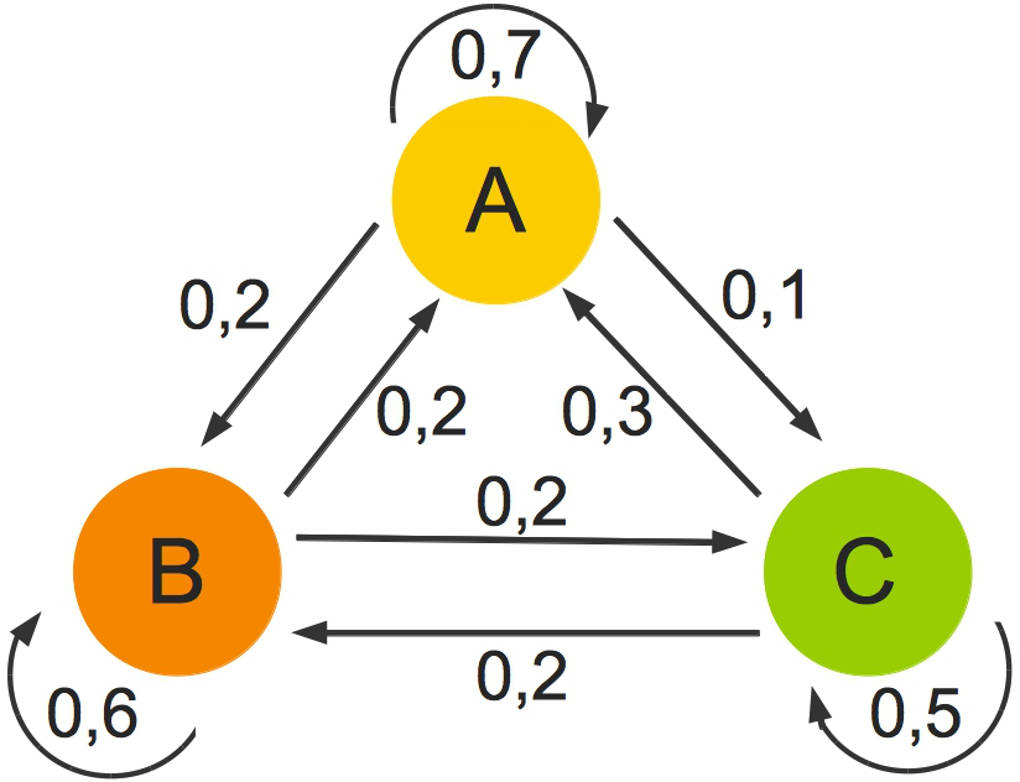
Dieses Diagramm kannst du wie folgt lesen:
- $70\%$ der Kunden von $A$, $60\%$ von $B$ und $50\%$ von $C$ bleiben dem entsprechenden Supermarkt treu.
- Von Supermarkt $A$ wandern $20\%$ nach $B$ und $10\%$ nach $C$ ab.
- Von Supermarkt $B$ wandern $20\%$ nach $A$ und $20\%$ nach $C$ ab.
- Von Supermarkt $C$ wandern $30\%$ nach $A$ und $20\%$ nach $B$ ab.
Erstellen einer Übergangsmatrix
Diese Bewegungen können in einer Übergangsmatrix $D$ dargestellt werden:
$D=\begin{pmatrix} 0,7&0,2&0,3 \\ 0,2&0,6&0,2 \\ 0,1&0,2&0,5 \\ \end{pmatrix}$.
Schauen wir einmal, was die Spalten und Zeilen bedeuten:
- Die Spalten der Matrix $D$ geben an, von welchem Supermarkt die Kunden wechseln. Die linke Spalte gehört zum Supermarkt $A$, die mittlere zu $B$ und die rechte zu $C$.
- Die Zeilen geben an, zu welchem Supermarkt die Kunden wechseln. Die erste Zeile bleibt/wechselt zu $A$, die zweite Zeile bleibt/wechselt zu $B$, die dritte Zeile bleibt/wechselt zu $C$.
Da die Anzahl der Kunden auch nach dem Wechsel immer gleich ist, ist die Summe der Elemente für jede Spalte immer $1$.
Mit Übergangsmatrizen rechnen
Wenn du die Anzahlen der Kunden in jedem Supermarkt zu Beginn einer Beobachtung kennst, kannst du die Anzahl nach einem Wechsel berechnen.
Sagen wir, je $1000$ Menschen sind Kunden in den drei Supermärkten. Zunächst notierst du die Anzahlen der Kunden in einem Vektor:
$\vec b=\begin{pmatrix}1000\\1000\\1000\end{pmatrix}$.
Nun kann die Matrix $D$ mit dem Vektor $\vec b$ multipliziert werden. Dabei multiplizierst du jede Zeile der Matrix $D$ mit dem Vektor $\vec b$:
$\begin{array}{lll} &&\begin{pmatrix} 0,7&0,2&0,3 \\ 0,2&0,6&0,2 \\ 0,1&0,2&0,5 \\ \end{pmatrix}\cdot \begin{pmatrix}\ 1000\\ 1000\\ 1000\end{pmatrix}\\ &=&\begin{pmatrix}\ 0,7\cdot 1000+0,2\cdot 1000+0,3\cdot 1000\\ 0,2\cdot 1000+0,6\cdot 1000+0,2\cdot 1000\\ 0,1\cdot 1000+0,2\cdot 1000+0,5\cdot 1000\end{pmatrix}\\ &=&\begin{pmatrix}\ 1200\\ 1000\\ 800\end{pmatrix} \end{array}$
Nach dem ersten Wechsel kaufen $1200$ Kunden in Supermarkt $A$, $1000$ in $B$ und $800$ in $C$ ein.
Natürlich kannst du ebenso die Zahl der Kunden nach einem weiteren Wechsel berechnen. Dazu werden die neuen Anzahlen in den Vektor $\vec b$ eingetragen und dieser noch einmal mit der Matrix $D$ multipliziert. Somit erhältst du $1280$ Kunden in Supermarkt $A$, $1000$ in $B$ und die verbleibenden $720$ in $C$.
Weitere Anwendungen für Matrizen
- Lineare Gleichungssysteme kannst du mit der Cramer’schen Regel lösen. Hierfür stellst du die Koeffizientenmatrix des linearen Gleichungssystems auf und berechnest die Lösungen mit der Determinante.
- Zu diesem Zweck kann auch das Gauß-Verfahren verwendet werden. Dieses Mal stellst du die erweiterte Koeffizientenmatrix auf und bringst diese auf obere Dreiecksgestalt.
Zuletzt wollen wir noch einmal nachvollziehen, wie aus einem linearen Gleichungssystem die Koeffizientenmatrix und schließlich die erweiterte Koeffizientenmatrix aufgestellt werden kann. Betrachte hierfür das lineare Gleichungssystem:
$\begin{array}{rclcrclcr} 3&\cdot&x&-&2&\cdot&y&=&8\\\ -2&\cdot&x&+&3&\cdot&y&=&-2 \end{array}$
Die Faktoren vor den Variablen werden als Koeffizienten bezeichnet.
Die Koeffizientenmatrix ist dann wie folgt gegeben:
$A=\begin{pmatrix} 3&-2 \\ -2&3 \end{pmatrix}$.
Wenn du als dritte Spalte noch die rechte Seite hinzufügst, erhältst du die erweiterte Koeffizientenmatrix.
$B=\begin{pmatrix} 3&-2 &|&8\\ -2&3&|&-2 \end{pmatrix}$.
Alle Lerntexte zum Thema
Lerntexte zum Thema
Grundlagen zu Matrizen (2 Lerntexte)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung











