Rotationsbewegung mit Drehimpuls und Kraft
Die Rotation als Analogie zur Translation mit Winkelgeschwindigkeit, Winkelbeschleunigung, Drehimpulserhaltung, Drehmoment und Rotationsenergie
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Einleitung
- Die Winkelgeschwindigkeit, -beschleunigung und Bahngeschwindigkeit
- Analogien zwischen Translation und Rotation
- Die Grundgleichung der Rotation
- Das Trägheitsmoment
- Der Drehimpuls
Einleitung
Ein Aspekt der Newton'schen Mechanik ist das Beschreiben von Rotationsbewegungen. Kreisbewegungen und die dabei wirkenden Kräfte begegnen dir häufig im Alltag wie beim Karussell auf dem Spielplatz oder bei den drehenden Reifen eines Fahrrads.

Eine wichtige physikalische Größe ist hierbei die Frequenz $f$ der Rotation. Sie gibt an, wie viele Umdrehung um die eigene Achse pro Sekunde ausgeführt werden. Die Umdrehungsdauer ist $T$ und es gilt $T=\frac1{f}$.
Rotiert wird üblicherweise in mathematisch positive Richtung also entgegen dem Uhrzeigersinn.
Die Winkelgeschwindigkeit, -beschleunigung und Bahngeschwindigkeit
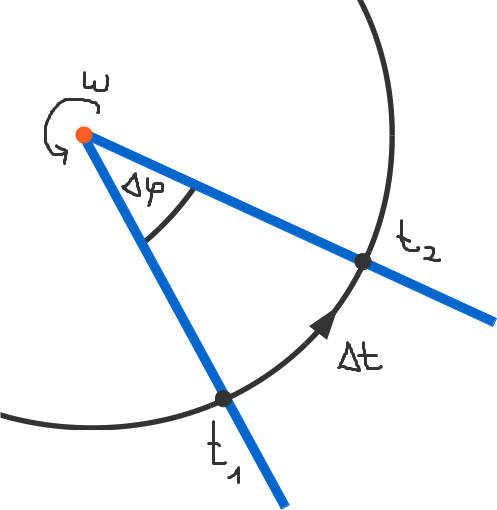
Zu Beginn etwas über die Grundlagen der Kreisbewegung: Bei einer Translation (geradlinigen Bewegung) mit einer Geschwindigkeit $v$ wird in einer bestimmten Zeit $t$ ein Weg $s$ zurückgelegt. Bei einer Kreisbewegung ist dies ähnlich: Hier wird pro Zeiteinheit $\Delta t$ ein Winkel $\Delta\varphi$ zurückgelegt. Analog zur Translation gibt der Quotient der beiden Größen die Geschwindigkeit an. Im Falle der Kreisbewegung spricht man von der Winkelgeschwindigkeit $\omega$ und es gilt
$\omega=\frac{\Delta \varphi}{\Delta t}.$
Die Änderung der Winkelgeschwindigkeit pro Zeit ist die Winkelbeschleunigung
$\alpha=\frac{\Delta\omega}{\Delta t}.$
Die Winkelgeschwindigkeit ist ein Maß dafür, wie schnell etwa ein Karussell auf dem Jahrmarkt um seine eigene Achse rotiert. Sicher ist dir auch aufgefallen, dass du dich schneller fortbewegst, wenn du dich weiter außen auf dem Karussell befindest (größerer Radius $r$). Du hast dann eine höhere Bahngeschwindigkeit $v$, die sich aus
$v=\omega\cdot r$
berechnet.
Analogien zwischen Translation und Rotation
Auch um weitere Größen und Formeln der Rotation einzuführen, kann man sich bei den Analogien bei Translation und Rotation bedienen. Du wirst sehen, dass die Gleichungen der Rotation die gleiche Struktur haben wie die Gleichungen der Translation.
Die Grundgleichung der Rotation
Um eine Masse zu beschleunigen muss eine Kraft wirken. Im Falle einer Kreisbewegung sorgt ein Drehmoment $M$ für die Winkelbeschleunigung. Die Grundgleichung der Rotation ist damit
$M=J\cdot\alpha.$
Vergleichst du diese Formel mit der dir bekannten Formel $F=m\cdot a$, so stellst du fest, dass $J$ das Äquivalent der Masse ist. $J$ ist das Trägheitsmoment.
Das Trägheitsmoment
Das Trägheitsmoment eines Körpers ist im Allgemeinen relativ kompliziert zu berechnen. Für Standardkörper wie Zylinder, Kugel o.ä. kannst du die Formeln allerdings nachschlagen. Das Trägheitsmoment ist ein Maß für den Widerstand eines Körpers gegen ein Drehmoment. Je größer das Trägheitsmoment ist, desto mehr Drehmoment ist nötig, um eine bestimmte Winkelbeschleunigung zu erreichen. Es hängt von der Drehachse und der Massenverteilung des Körpers ab.
Der Drehimpuls
Der Impuls der Translation ist das Produkt aus Masse und Geschwindigkeit $p=m\cdot v$. Analog kannst du den Drehimpuls $L$ eines starren Körpers angeben.
$L=J\cdot\omega$
Natürlich ist auch bei der Kreisbewegung der Impuls erhalten, man spricht von Drehimpulserhaltung.
Du kannst dich davon sofort überzeugen, wenn du gerade auf einem drehbaren Bürostuhl sitzt. Wenn du dich mit einer bestimmten Winkelgeschwindigkeit drehst und dann die Beine ausstreckst, wirst du langsamer. Durch das Beine ausstrecken hast du nämlich dein Trägheitsmoment vergrößert. Da $L$ konstant ist, muss sich also deine Drehgeschwindigkeit reduzieren.
Die Rotationsernergie
Eine Rotation ist im Grunde nur eine besondere Form der Bewegung, folglich muss auch eine Rotation Bewegungsenergie (kinetische Energie) speichern. Stell dir einen rotierenden Körper als unzählige rotierende Massepunkte vor.
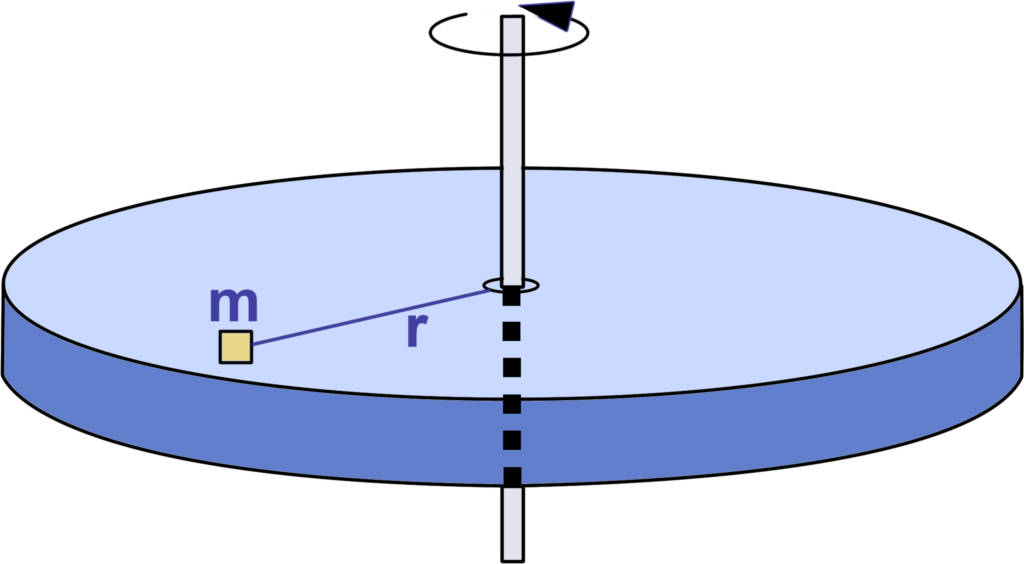
Die Rotationsenergie ist dann die Summe aller kinetischen Energien der einzelnen Massenpunkte. Verwendest du wieder die Analogien, so erhältst du
$E_{\text{rot}}=\sum_i \frac12 m_i v_i^2=\frac12 J \omega^2.$
In der Praxis verwendet man beispielsweise rotierende Schwungräder als Energiespeicher.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Rotationsbewegung mit Drehimpuls und Kraft (8 Videos, 3 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Rotationsbewegung mit Drehimpuls und Kraft (10 Arbeitsblätter)
-
 Zeit-Bahngrößen-Gesetze der Rotation
PDF anzeigen
Zeit-Bahngrößen-Gesetze der Rotation
PDF anzeigen -
 Winkelbeschleunigung α
PDF anzeigen
Winkelbeschleunigung α
PDF anzeigen -
 Drehimpuls L
PDF anzeigen
Drehimpuls L
PDF anzeigen -
 Impulserhaltung bei der Kreisbewegung
PDF anzeigen
Impulserhaltung bei der Kreisbewegung
PDF anzeigen -
 Drehmoment M
PDF anzeigen
Drehmoment M
PDF anzeigen -
 Trägheitsmoment J
PDF anzeigen
Trägheitsmoment J
PDF anzeigen -
 Rotationsenergie
PDF anzeigen
Rotationsenergie
PDF anzeigen -
 Grundgesetz der Dynamik der Rotation
PDF anzeigen
Grundgesetz der Dynamik der Rotation
PDF anzeigen -
 Corioliskraft und foucaultsches Pendel
PDF anzeigen
Corioliskraft und foucaultsches Pendel
PDF anzeigen -
 Fliehkraft, eine Scheinkraft – Zentrifugalkraft und Zentripetalkraft
PDF anzeigen
Fliehkraft, eine Scheinkraft – Zentrifugalkraft und Zentripetalkraft
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie






















