Grenzwerte von Folgen

Inhaltsverzeichnis zum Thema

• Was sind Folgen?
• Grenzwerte von Folgen
  • Konvergente Folgen
  • Divergente Folgen
• Grenzwertsätze von Folgen

Was sind Folgen?

Unter einer Folge $(a_n)$ kannst du dir eine Auflistung von z.B. Zahlen, Funktionen oder Mengen vorstellen. Die einzelnen Folgeglieder $a_n$ sind dabei fortlaufend nummeriert. Dabei gilt: $n\in\mathbb{N}_0$.

Fortan werden nur noch Zahlenfolgen betrachtet. Die einzelnen Glieder folgen meist nicht zufällig aufeinander. Sie können durch eine Bildungsvorschrift bestimmt werden:

$\begin{array}{lcllll} g_n=\frac{1}{n} &\Rightarrow & g_1=\frac{1}{1} & g_2=\frac{1}{2}& g_3=\frac{1}{3}& …\\ b_n=(-1)^n\cdot\frac{1}{n} &\Rightarrow & b_1=-\frac{1}{1}& b_2=\frac{1}{2}& b_3=-\frac{1}{3}& …\\ c_n=n^2&\Rightarrow & c_1=1 & c_2=4 & c_3=9 & …\\ d_n=(-1)^n \cdot n &\Rightarrow & d_1=-1 & d_2=2 & d_3 = -3 & …\\ e_n=(1+\frac{1}{n})^n &\Rightarrow & e_1=2 & e_2=\frac{9}{4}& e_3=\frac{64}{27}& …\\ \end{array}$

Die Folgen $(b_n)$ und $(d_n)$ nennt man auch alternierende Folgen. Dabei sind die Folgeglieder abwechselnd positiv und negativ. Die Folge $(e_n)$ ist eine ganz besondere Folge. Warum das so ist, erfährst du später.

Die einzelnen Folgeglieder kannst du auch als Punkte in ein Koordinatensystem eintragen. Beachte: Die Definitionsmenge von Folgen ist immer eine Teilmenge von $\mathbb{N}_0$. Deshalb darfst du die Punkte nicht miteinander verbinden.

Sieh dir nun die Folge $(g_n)$ genauer an. Was kannst du dabei feststellen?

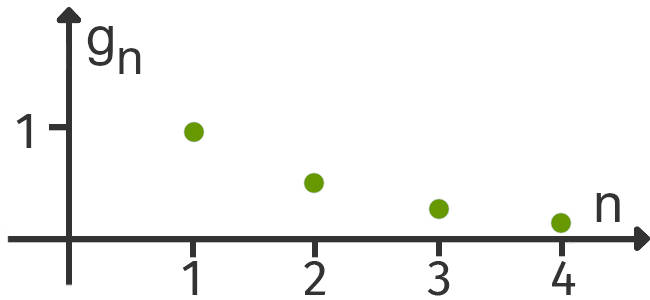
Ganz genau! Der Betrag der Folgeglieder wird immer kleiner. Sogar unendlich klein. Was genau im Unendlichen passiert, kannst du mit der Bestimmung des Grenzwerts herausfinden.

Grenzwerte von Folgen

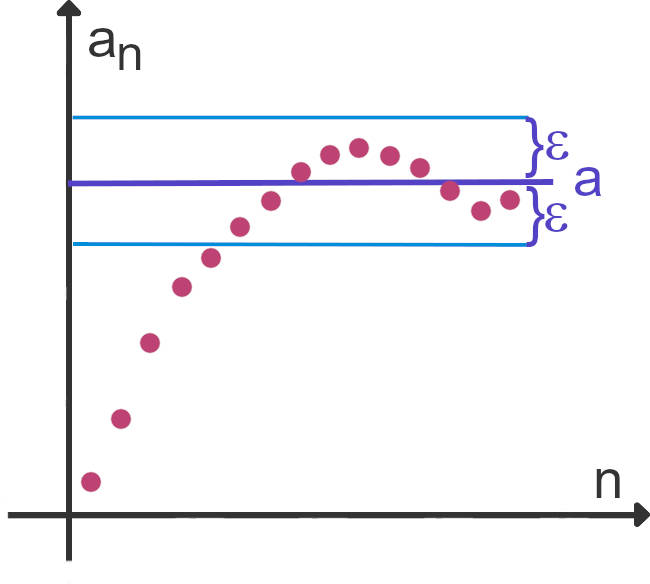
Der Grenzwert einer Folge $(a_n)$ ist die Zahl $a$, wenn es zu jedem noch so kleinen $\varepsilon\gt 0$ einen Index $N$ gibt, sodass alle Folgeglieder nach diesem Index innerhalb der Umgebung von $\varepsilon$ um $a$ liegen. Es gilt also:

$\bigl|a_n-a\bigl|\lt \varepsilon\quad\text{für alle}\quad n\gt N\quad n\in\mathbb{N}\quad N\in\mathbb{N}_0$

Konvergente Folgen

Wenn ein solcher Grenzwert existiert, ist die Folge konvergent. Da die Folgeglieder von $(g_n)$ ohne Ausnahme betragsmäßig immer kleiner werden, gilt:

$g_n=\frac{1}{n}\quad\Rightarrow\quad \lim\limits_{n \rightarrow \infty}{(g_n)}=0$

Auch bei der alternierenden Folge $(b_n)$ nähern sich die Folgeglieder der $0$ an. Die Folgeglieder „springen“ um den Wert $0$ und kommen ihm dabei immer näher:

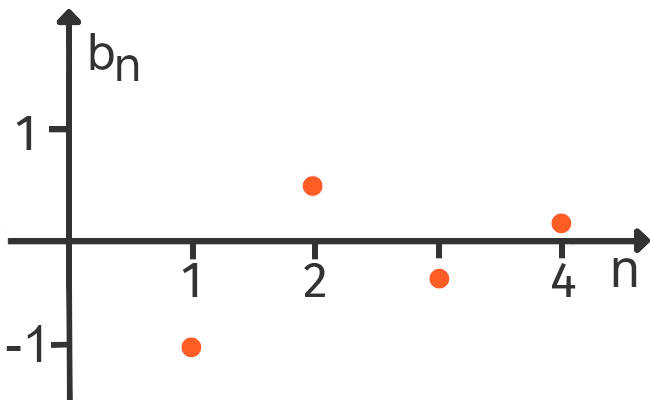
$b_n=(-1)^n\cdot \frac{1}{n}\quad\Rightarrow\quad \lim\limits_{n \rightarrow \infty}{(b_n)}=0$

Divergente Folgen

Es gibt allerdings auch Folgen, deren Glieder nicht zu einem bestimmten Wert streben. Diese Folgen nennt man divergent.

Die Folge $(c_n)$ mit der Bildungsvorschrift $c_n=n^2$ ist so eine divergente Folge, denn die Folgeglieder werden immer größer. Sie gehen also ins Unendliche. Da unendlich keine bestimmte Zahl ist, ist dies auch kein Grenzwert.

Ebenso ist die alternierende Folge $(d_n)$ mit $d_n=(-1)^n\cdot n$ divergent. Die aufeinanderfolgenden Glieder entfernen sich immer weiter voneinander. Die Glieder mit geradem Index werden immer größer und streben Richtung $+\infty$. Die Ungeraden dagegen streben Richtung $-\infty$.

Den Grenzwert für kompliziertere, aus den Grundrechenarten zusammengesetzte Folgen kannst du oft ganz einfach bestimmen. Dabei helfen dir die Grenzwertsätze:

Grenzwertsätze von Folgen

Wenn zwei Folgen $(a_n)$ und $(b_n)$ konvergent sind mit den Grenzwerten $a$ und $b$, dann gilt:

$\begin{array}{llclcll} \text{(1)} &\lim\limits_{n \rightarrow \infty}{(a_n)\pm (b_n)} &=& \lim\limits_{n \rightarrow \infty}{(a_n)}+ \lim\limits_{n \rightarrow \infty}{(b_n)} &=& a\pm b & \\ \\ \text{(2)} &\lim\limits_{n \rightarrow \infty}{(a_n)\cdot (b_n)} &=& \lim\limits_{n \rightarrow \infty}{(a_n)}\cdot\lim\limits_{n \rightarrow \infty}{(b_n)} &=&a\cdot b & \\ \\ \text{(3)} &\lim\limits_{n \rightarrow \infty}{\frac{(a_n)}{(b_n)}} &=&\dfrac{\lim\limits_{n \rightarrow \infty}{(a_n)}}{\lim\limits_{n \rightarrow \infty}{(b_n)}} &=&\frac{a}{b} & \text{mit} \nobreakspace b_n,b\neq0 \\ \end{array}$

Das bedeutet, dass die Summen-, Differenzen- und Produktfolgen von zwei konvergenten Folgen ebenfalls konvergent sind. Der gesamte Grenzwert errechnet sich dann durch Addition, Subtraktion oder Multiplikation der einzelnen Grenzwerte. Falls der Grenzwert der Folge $(b_n)$ sowie alle Folgeglieder $b_n$ ungleich $0$ sind, gilt dies auch für die Division.

Nun aber zurück zur besonderen Folge $(e_n)$. Wenn $n$ gegen unendlich läuft, kann man die Folge als unendliches Produkt auffassen:

$e_n=(1+\frac{1}{n})^n=\underbrace{(1+\frac{1}{n})\cdot(1+\frac{1}{n})\cdot\ …\ \cdot(1+\frac{1}{n})}_{n\text{-mal}}$

Sieh dir nun die Folge $(f_n)$ an:

$f_n=(1+\frac{1}{n})\cdot (1+\frac{1}{n})$

Du kannst bei dieser die Grenzwertsätze anwenden:

$\begin{array}{rcl} \lim\limits_{n \rightarrow \infty}{(1+\frac{1}{n})^2}&=&( \lim\limits_{n \rightarrow \infty}{1}+\lim\limits_{n \rightarrow \infty}{\frac{1}{n}})\cdot (\lim\limits_{n \rightarrow \infty}{1}+\lim\limits_{n \rightarrow \infty}{\frac{1}{n}})\\ &=& (1+0)\cdot (1+0) \\ &=& 1 \end{array}$

Tatsächlich haben alle endlichen Produktfolgen dieser Form den Grenzwert $1$. Für das unendliche Produkt kannst du aber die Grenzwertsätze so nicht anwenden. Dieses strebt gegen einen anderen Wert:

$\lim\limits_{n \rightarrow \infty}{(1+\frac{1}{n})^n}=e\approx 2,7182$

Die Zahl $e$ nennt man auch Eulersche Zahl.