Betrag eines Vektors


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Betrag eines Vektors
Nach dem Schauen dieses Videos wirst du in der Lage sein, den Betrag und damit die Länge eines Vektors zu berechnen. Auf die gleiche Art und Weise kann man auch den Abstand zwischen zwei Punkten bestimmen. Außerdem erfährst du, was ein Einheitsvektor ist und wie man ihn ermittelt.

Zunächst schauen wir uns an, wie man mit Hilfe des Satzes des Pythagoras die Länge einer Raumdiagonale ermittelt. Anschließend werden wir dieses Wissen anwenden, um die Länge eines Vektors zu bestimmen Abschließend erfährst du, was es mit den sogenannten Einheitsvektoren auf sich hat.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Betrag, Betragsstriche, Länge, Maßeinheit, Vektor, Nullvektor, Einheitsvektor, Satz des Pythagoras.
Bevor du dieses Video schaust, solltest du bereits den Satz des Pythagoras kennen und wissen, was ein Vektor ist.
Nach diesem Video wirst du darauf vorbereitet sein, mehr über Vektoren zu lernen.
Transkript Betrag eines Vektors
Was surrt denn hier? Sind es die mutierten Spinnen-Mäuse? Schlimmer - am anderen Ende des Raumes sitzt eine Mücke. So ein Biest. Schnell erschlagen das Ding! Aber wie? Nichts leichter als das - zumindest wenn man sich mit dem „Betrag eines Vektors“ auskennt. So eine Jagd kann anstrengend und zermürbend sein. Das Problem ist nämlich: wenn man erstmal um den Experimentiertisch herumgelaufen ist, um dann das surrende Scheusal oben in der Ecke zum Schweigen zu bringen, ist das Mistviech schon wieder ganz woanders hingeflogen. Zielführender wäre es, dem Ding auf direktem Wege den Garaus zu machen, oder? Schauen wir uns an, wie sich das mathematisch vereinfachen lässt. Der Weg um den Tisch herum und nach oben zur Decke ist fast zehn Meter lang. Den direkten Weg, also die Raumdiagonale quer durchs Labor können wir mit dem Satz des Pythagoras berechnen. Die Flächendiagonale ist fünf Meter lang. Nun wenden wir den Satz des Pythagoras ein zweites Mal an und erhalten ungefähr 5,7 Meter. Vielleicht hast du es schon gemerkt: Wir hätten die Rechnerei auch viel kürzer machen können - einfach alle drei Längen quadrieren, addieren und dann die Wurzel ziehen. Damit kommen wir auf das gleiche Ergebnis, aber zweifellos schneller. Der direkte Weg ist also wesentlich kürzer und die Erfolgsquote, das Biest ein für alle Mal zu erledigen, hoffentlich um einiges höher. Und was hat das Ganze jetzt mit Vektoren zu tun? Auch Vektorpfeile verlaufen oft quer durch den dreidimensionalen Raum, und um ihre Länge zu bestimmen, wenden wir den Satz des Pythagoras auf die gleiche Art und Weise wie eben an. Zum Beispiel bei diesem Vektor vom Punkt P „drei, null, null“ zum Punkt Q „null, vier, zwei Komma sieben fünf“. Zur Erinnerung: Man bestimmt den Vektor PQ, indem man die Koordinaten des Anfangspunktes P von den Koordinaten des Endpunktes Q subtrahieren. In unserem Fall erhalten wir den Vektor „minus drei, vier, zwei Komma sieben fünf“. Der Vektor P-Q verläuft also drei Schritte nach hinten, vier nach rechts und 2,75 nach oben. Die Länge des Vektorpfeils, also den Abstand zwischen P und Q, können wir wieder mit dem Satz des Pythagoras ausrechnen. Dafür setzen wir die einzelnen Vektoreinträge für a, b und c ein, und berechnen d. Da alle Zahlen quadriert werden, ist die Maßzahl, die wir für d erhalten immer positiv. Das kennen wir bereits vom Betrag, der ja auch immer positiv ist. Deshalb wird die Länge eines Vektorpfeils auch als Betrag des Vektors bezeichnet, und man nutzt die Betragsstriche als Schreibweise. Da unsere Maßeinheit normalerweise die Koordinateneinheit ist, müssen wir beim Ergebnis keine Längeneinheit angeben. Der Gegenvektor q-p hat logischerweise dieselbe Länge wie der Vektor p-q, da der Abstand der beiden Punkte P und Q natürlich gleich groß bleibt. Das kannst du gerne selbst nachrechnen. Der Nullvektor hat - wie kann es anders sein? - die Länge null. Die Berechnung ist in diesem Fall natürlich ein Kinderspiel. Für alle anderen Fälle gibt es bei C-A-S-Rechnern übrigens auch gesonderte Befehle, um den Betrag eines Vektors auszurechnen. Meistens gibt es sogar verschiedene Möglichkeiten für Eingabe und Berechnung. Schauen wir uns ein weiteres Beispiel nochmal genauer an. Der Vektor v hat die Länge „Wurzel aus sechsundzwanzig“. Das sind ungefähr 5,1 Längeneinheiten. Für manche Aufgaben brauchen wir jedoch Vektoren, die in die gleiche Richtung zeigen, und dabei genau die Länge „eins“ haben. Solche Vektoren werden Einheitsvektoren genannt. Anders als bei diesem Namen vermutet, werden sie in der Mathematik sehr uneinheitlich bezeichnet. Um unseren Vektor v also zum Einheitsvektor „v-E“ zu machen, müssen wir ihn auf die Länge „eins“ schrumpfen. Dafür teilen wir ihn durch seine Länge. Das schreibt man gewöhnlich so auf. Um den Vorfaktor bei längeren Rechnungen nicht aus den Augen zu verlieren, kann man ihn auch in die Klammer ziehen. Auch hier ist der Taschenrechner unser bester Freund. Auf diese Weise können wir alle Vektoren auf die Länge „eins“ bringen, sie also normieren. Deshalb spricht man beim Einheitsvektor auch vom „normierten Vektor“. Jeder Vektor hat daher seinen eigenen Einheitsvektor und dieser Vektor mit seinen krummen Einträgen hat wirklich die Länge „eins“. Falls du das nicht glaubst, weißt du ja jetzt, wie du das überprüfen kannst. Und wir ziehen kurz ein Resümee. Unter dem Betrag eines Vektors verstehen wir die Länge der zum Vektor zugehörigen Pfeile. Bei der Schreibweise verwenden wir die Betragsstriche, und zur Berechnung nutzen wir den Satz des Pythagoras. Auf die gleiche Weise können wir auch den Abstand zwischen zwei Punkten berechnen. Vektor und Gegenvektor haben immer die gleiche Länge. Und der Nullvektor hat die Länge Null. Wenn wir einen gegeben Vektor auf die Länge eins normieren, bilden wir den sogenannten Einheitsvektor. Und gegen lästige Biester helfen mutierte Frösche mit pfeilschneller Zunge.
Betrag eines Vektors Übung
-
Gib an, welche Aussagen zum Betrag von Vektoren richtig sind.
TippsDer Betrag eines Vektors ist gleich der Länge des zugehörigen Vektorpfeils. Zur Berechnung wird der Satz des Pythagoras verwendet.
Zur Berechnung des Einheitsvektors dividieren wir den Vektor durch seine Länge. Dies wird auch als Normierung des Vektors bezeichnet.
LösungDer Betrag eines Vektors ist gleich der Länge des zugehörigen Vektorpfeils. Zur Berechnung wird der Satz des Pythagoras verwendet.
Die Länge eines Vektors ist immer positiv.
Diese Aussage ist richtig, da alle Koordinaten bei der Rechnung quadriert werden.Die Länge eines Vektors ist gleich der Länge seines Gegenvektors.
Diese Aussage ist richtig, da der Abstand der beiden Endpunkte gleich groß ist.Wir können jeden beliebigen Vektor auf die Länge $1$ normieren. Wir erhalten dann den zugehörigen Einheitsvektor. Zur Berechnung des Einheitsvektors dividieren wir den Vektor durch seine Länge.
Ein Einheitsvektor hat die Länge $0$.
Diese Aussage ist falsch. Ein Einheitsvektor hat die Länge $1$, da der Vektor durch seine Länge geteilt wird.Durch das Normieren wird ein Vektor kürzer.
Diese Aussage ist falsch. Hat der Vektor eine Länge kleiner als $1$, so wird er beim Normieren länger. Hat der Vektor eine Länge größer als $1$, so wird er beim Normieren kürzer. -
Beschreibe, was man unter dem Betrag eines Vektors versteht.
TippsEin Einheitsvektor ist ein Vektor mit der Länge $1$.
Wir können die Länge der Raumdiagonalen mithilfe zwei rechtwinkliger Dreiecke berechnen.
LösungVektorpfeile verlaufen häufig im dreidimensionalen Raum und werden durch ihre Richtung und ihre Länge definiert.
Betrag eines Vektors:
Der Betrag eines Vektors ist gleich der Länge des zugehörigen Vektorpfeils. Zur Berechnung wird der Satz des Pythagoras verwendet.
Beispiel: Der Betrag des Vektors $\vec{v}$ schreiben wir als $|\vec{v}|$. Wir betrachten den folgenden Vektor:
$\vec{v} =\left( \begin{array}{c} 4 \\ -1 \\ 8 \\ \end{array}\right)$
Wir berechnen seinen Betrag wie folgt:
$|\vec{v}| = \left| \left( \begin{array}{c} 4 \\ -1 \\ 8 \\ \end{array}\right) \right| = \sqrt{4^2+(-1)^2+8^2} = 9$Einheitsvektoren:
Wir können jeden beliebigen Vektor auf die Länge $1$ normieren. Wir erhalten dann den zugehörigen Einheitsvektor. Zur Berechnung des Einheitsvektors dividieren wir den Vektor durch seine Länge.
Beispiel: Der Einheitsvektor des Vektors $\vec{v}$ ist:
$\vec{v}_E = \dfrac{1}{9}\left( \begin{array}{c} 4 \\ -1 \\ 8 \\ \end{array}\right)$
Wir können den Faktor auch in die Klammer ziehen und erhalten damit:
$\vec{v}_E = \left( \begin{array}{c}\frac{4}{9} \\ -\frac{1}{9} \\ \frac{8}{9} \\ \end{array}\right)$ -
Berechne die Länge der Vektoren.
TippsWir berechnen die Länge eines Vektors allgemein wie folgt:
$d = \sqrt{a^2+b^2+c^2}$
Dabei sind $a$,$b$,$c$ die Einträge des Vektors und $d$ die Länge des Vektors.
In diesem Bild wird die Länge des Vektors $\overrightarrow{PQ}= \begin{pmatrix} -3 \\ 4 \\ 2{,}75 \end{pmatrix}$ und des Gegenvektors ausgerechnet.
LösungDer Betrag eines Vektors ist gleich der Länge des zugehörigen Vektorpfeils. Zur Berechnung verwenden wir den Satz des Pythagoras:
Den Betrag des Vektors $\vec{v}$ schreiben wir als $|\vec{v}|$.Wir berechnen somit die folgenden Beträge bzw. Längen:
Erste Aufgabe:
$\vec{v} = \left( \begin{array}{c} 1 \\ 4 \\ 5 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{1^2+4^2+5^2} = \sqrt{42} \approx 6,5$Zweite Aufgabe:
$\vec{v} = \left( \begin{array}{c} 2 \\ 2 \\ 8 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{2^2+2^2+8^2} = \sqrt{72} \approx 8,5$Dritte Aufgabe:
$\vec{v} = \left( \begin{array}{c} 3 \\ -4 \\ -7 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{3^2+(-4)^2+(-7)^2} = \sqrt{74} \approx 8,6$Vierte Aufgabe:
$\vec{v} = \left( \begin{array}{c} -2 \\ 5 \\ 9 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{(-2)^2+5^2+9^2} = \sqrt{110} \approx 10,5$ -
Stelle den Einheitsvektor der Vektoren auf.
TippsWir können jedem Vektor seinen Einheitsvektor zuordnen, indem wir den Vektor durch seine Länge teilen.
Beispiel: $\left( \begin{array}{c} 2 \\ -9 \\ 1 \\ \end{array}\right) $
Länge: $\left| \left( \begin{array}{c} 2 \\ -9 \\ 1 \\ \end{array}\right) \right| = \sqrt{2^2+(-9)^2+1^2} = \sqrt{86} $
Einheitsvektor: $\left( \begin{array}{c} \frac{2}{\sqrt{86}} \\ \frac{-9}{\sqrt{86}}\\ \frac{1}{\sqrt{86}} \\ \end{array}\right) $LösungWir können jedem Vektor seinen Einheitsvektor zuordnen, indem wir den Vektor durch seine Länge teilen. Der Einheitsvektor hat somit immer die Länge $1$.
Wir bestimmen also zunächst mit dem Satz des Pythagoras die Länge jeden Vektors und dividieren anschließend jede Koordinate durch diese Länge:
Erster Vektor: $\left( \begin{array}{c} 1 \\ -3 \\ 5 \\ \end{array}\right) $
Länge: $\left| \left( \begin{array}{c} 1 \\ -3 \\ 5 \\ \end{array}\right) \right| = \sqrt{1^2+(-3)^2+5^2} = \sqrt{35}$
Einheitsvektor: $\frac{1}{\sqrt{35}} \cdot \left( \begin{array}{c} 1 \\ -3 \\ 5 \\ \end{array}\right) = \left( \begin{array}{c} \frac{1}{\sqrt{35}} \\ -\frac{3}{\sqrt{35}} \\ \frac{5}{\sqrt{35}} \\ \end{array}\right) $Zweiter Vektor: $\left( \begin{array}{c} 3 \\ \sqrt{2} \\ -5 \\ \end{array}\right) $
Länge: $\left| \left( \begin{array}{c} 3 \\ \sqrt{2} \\ -5 \\ \end{array}\right) \right| = \sqrt{3^2+\sqrt{2}^2+(-5)^2} = \sqrt{36} =6$
Einheitsvektor: $\frac{1}{6} \cdot \left( \begin{array}{c} 3 \\ \sqrt{2} \\ -5 \\ \end{array}\right) = \left( \begin{array}{c} 0{,}5 \\ \frac{\sqrt{2}}{6} \\ -\frac{5}{6}\\ \end{array}\right) $Dritter Vektor: $\left( \begin{array}{c} 0 \\ -6 \\ 8 \\ \end{array}\right) $
Länge: $\left| \left( \begin{array}{c} 0 \\ -6 \\ 8 \\ \end{array}\right) \right| = \sqrt{0^2+(-6)^2+8^2} = \sqrt{100} =10$
Einheitsvektor: $\frac{1}{10} \cdot \left( \begin{array}{c} 0 \\ -6 \\ 8 \\ \end{array}\right) = \left( \begin{array}{c} 0 \\ -0{,}6 \\ \frac{4}{5} \\ \end{array}\right) $Vierter Vektor: $\left( \begin{array}{c} 3 \\ 9 \\ 2 \\ \end{array}\right) $
Länge: $\left| \left( \begin{array}{c} 3 \\ 9 \\ 2 \\ \end{array}\right) \right| = \sqrt{3^2+9^2+2^2} = \sqrt{94} $
Einheitsvektor: $ \frac{1}{\sqrt{94}} \cdot \left( \begin{array}{c} 3 \\ 9 \\ 2 \\ \end{array}\right) = \left( \begin{array}{c} \frac{3}{\sqrt{94}} \\ \frac{9}{\sqrt{94}}\\ \frac{2}{\sqrt{94}} \\ \end{array}\right) $ -
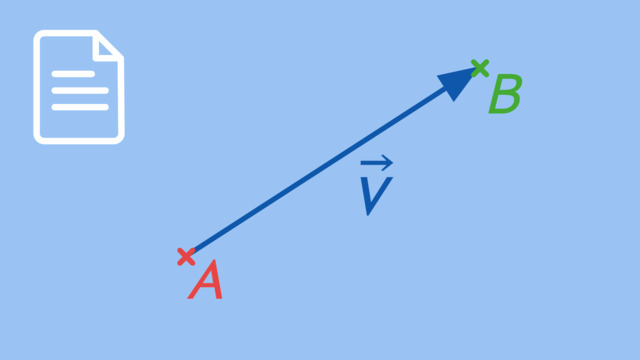
Bestimme den Vektor $\overrightarrow{AB}$.
TippsDer Vektor $\overrightarrow{PQ}$ zeigt vom Punkt $P$ zu Punkt $Q$. Das gleiche Prinzip können wir auf den Vektor $\overrightarrow{AB}$ und den Punkten $A$ und $B$ anwenden.
Beispiel:
$A(1|-1|5) \quad B(3|0|-2)$$ \overrightarrow{AB} =\left( \begin{array}{c} 3-1 \\ 0-(-1) \\ -2-5 \\ \end{array}\right) =\left( \begin{array}{c} 2 \\ 1 \\ -7 \\ \end{array}\right)$
LösungAllgemein können wir einen Vektor $\overrightarrow{AB}$ im dreidimensionalen zwischen zwei gegebenen Punkten $A(a_1| a_2| a_3)$ und $B(b_1|b_2|b_3)$ wie folgt bestimmen:
$\overrightarrow{AB} =\left( \begin{array}{c} b_1-a_1 \\ b_2-a_2 \\ b_3-a_3 \\ \end{array}\right)$
Wir berechnen so die folgenden Vektoren:
Erster Vektor: $A(3|-4|2), ~ B(1|0|-5)$
$ \overrightarrow{AB} =\left( \begin{array}{c} 1-3 \\ 0-(-4) \\ -5-2 \\ \end{array}\right) =\left( \begin{array}{c} -2 \\ 4 \\ -7 \\ \end{array}\right)$
Zweiter Vektor: $A(1|0|-5), ~ B(3|-4|2) $
$ \overrightarrow{AB} =\left( \begin{array}{c} 3-1 \\ -4-0 \\ 2-(-5) \\ \end{array}\right) =\left( \begin{array}{c} 2 \\ -4 \\ 7 \\ \end{array}\right)$
Dritter Vektor: $A(-1|5|2), ~ B(-1|3|-4)$
$ \overrightarrow{AB} =\left( \begin{array}{c} -1-(-1) \\ 3-5 \\ -4-2 \\ \end{array}\right) =\left( \begin{array}{c} 0 \\ -2 \\ -6 \\ \end{array}\right)$
Vierter Vektor: $A(0|-3|1), ~ B(1|1|-3) $
$ \overrightarrow{AB} =\left( \begin{array}{c} 1-0 \\ 1-(-3) \\ -3-1\\ \end{array}\right) =\left( \begin{array}{c} 1 \\ 4 \\ -4 \\ \end{array}\right)$
-
Ordne die Vektoren nach ihrer Länge.
TippsBeachte:
$(\sqrt{7})^2=7$
$(-3)^2=+9$
Berechne zuerst die Längen der einzelnen Vektoren:
$\vec{v} = \left( \begin{array}{c} a \\ b \\ c \\ \end{array}\right) \quad | \vec{v} | = \sqrt{a^2+b^2+c^2}$
LösungWir können die Länge bzw. den Betrag eines Vektors mit Hilfe des Satz des Pythagoras berechnen. Dazu ziehen wir die Wurzel aus der Summe der quadrierten Koordinaten.
Um die Vektoren nach ihrer Länge ordnen zu können, berechnen wir zunächst die Länge der einzelnen Vektoren:
- $\vec{v} = \left( \begin{array}{c} 0 \\ 3 \\ 2 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{0^2+3^2+2^2} = \sqrt{13} $
- $\vec{v} = \left( \begin{array}{c} \sqrt{2} \\ \sqrt{6} \\ 3 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{\sqrt{2}^2+\sqrt{6}^2+3^2} = \sqrt{17} $
- $\vec{v} = \left( \begin{array}{c} -1 \\ 3 \\ -3 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{(-1)^2+3^2+(-3)^2} = \sqrt{19} $
- $\vec{v} = \left( \begin{array}{c} -4 \\ \sqrt{3} \\ 0{,}1 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{(-4)^2+\sqrt{3}^2+0{,}1^2} = \sqrt{19{,}01} $
- $\vec{v} = \left( \begin{array}{c} -5 \\ -1 \\ -1 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{(-5)^2+(-1)^2+(-1)^2} = \sqrt{27} $
- $\vec{v} = \left( \begin{array}{c} 4 \\ -2 \\ 3 \\ \end{array}\right) \quad | \vec{v} | = \sqrt{4^2+(-2)^2+3^2} = \sqrt{29} $
Der Wert einer Wurzel ist umso größer, je größer der Radikand (Wert unter der Wurzel) ist. Daher gilt:
$\sqrt{13} < \sqrt{17} < \sqrt{19} < \sqrt{19{,}01} < \sqrt{27} < \sqrt{29} $
Somit können wir die Vektoren wie folgt ordnen:
$\left| \left( \begin{array}{c} 0 \\ 3 \\ 2 \\ \end{array}\right) \right| < \left| \left( \begin{array}{c} \sqrt{2} \\ \sqrt{6} \\ 3 \\ \end{array}\right) \right| < \left| \left( \begin{array}{c} -1 \\ 3 \\ -3 \\ \end{array}\right) \right| < \left| \left( \begin{array}{c} -4 \\ \sqrt{3} \\ 0{,}1 \\ \end{array}\right) \right| < \left| \left( \begin{array}{c} -5 \\ -1 \\ -1 \\ \end{array}\right) \right| < \left| \left( \begin{array}{c} 4 \\ -2 \\ 3 \\ \end{array}\right) \right| $
9.728
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.283
Lernvideos
38.567
Übungen
33.604
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?

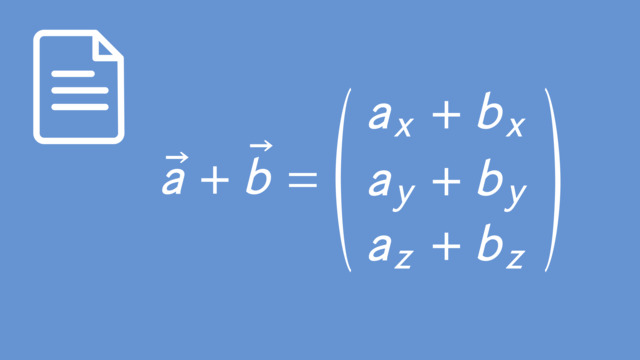









man, da habe ich aber mehr erwartet von dieser Seite bei dem Preis.
Es gibt ja kein einziges Arbeitsblatt zum Thema Vektoren.
Enttäuschend