Scharen von Wurzelfunktionen – Kurvendiskussion


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Scharen von Wurzelfunktionen – Kurvendiskussion
Hallo, ich bin Frank. Du erfährst heute von mir, wie man mit Funktionen, die einen Wurzelausdruck und einen Parameter enthalten, eine Kurvendiskussion durchführt. Funktionen mit einem Parameter nennt man Kurvenscharen. Du solltest bereits die Bestandteile einer Kurvendiskussion kennen und dich auch mit Wurzelfunktionen auskennen. Wir wiederholen zusammen die einzelnen Bestandteile der Kurvendiskussion. Ich erkläre dir, was man bei einer Kurvendiskussion mit einem Parameter und im Speziellen mit Funktionen mit Wurzelausdrücken beachten muss. Das Ziel der Kurvendiskussion ist es eine ungefähre Skizze der Funktion mit seinen wichtigsten Bestandteilen zu erhalten. Da wir hier aber durch den Parameter eine Kurvenschar haben, skizzieren wir spezielle Funktionen der Kurvenschar, indem wir vorher Werte für den Parameter auswählen. Am Ende wirst du staunen, was du alles schon kannst und was du neu dazu gelernt hast. Viel Spaß mit Wurzeln, Kurvendiskussion und Parametern.
Transkript Scharen von Wurzelfunktionen – Kurvendiskussion
Hallo, mein Name ist Frank und ich werde in diesem Video eine Kurvendiskussion mit einer Wurzelfunktion mit einem Parameter durchführen. Die einzelnen Punkte der Kurvendiskussion findest du hier auf der rechten Seite. Die Funktion, die ich betrachte, lautet fa(x)= √(x+a) - (x+a). Du siehst, hier ist ein Parameter in der Funktion drin und wie der sich auf die Funktion auswirken wird, das werden wir jetzt im Laufe dieses Videos sehen. Ich fange an mit dem Definitionsbereich. Für den Definitionsbereich muss der Term unter der Wurzel größer/gleich null sein. Ich schreibe mal auf x + a ≥ 0. Und das kann ich äquivalent umformen zu x ≥ -a. Das heißt, der Definitionsbereich ist die Menge der reellen Zahlen, welche größer/gleich minus a sind. Da dieser Definitionsbereich nicht symmetrisch ist, haben wir hier auch keine Symmetrie. Zu den Ableitungen, die erste Ableitung bekomme ich durch Ableitung der Wurzelfunktion, die Ableitung von Wurzeln ist eins geteilt durch zweimal Wurzel. Und der innere Term bleibt einfach stehen. Und die Ableitung von diesem Term ist eins, der Parameter a fällt hier beim Ableiten raus. Zweite Ableitung ist dann -1 / (4√(x+a)³). Jetzt schaue ich mir die Achsenschnittpunkte an, ich gucke erstmal die Nullstellen. Also fa(x) = 0. Das ist äquivalent dazu, dass Wurzel aus, ich schreibe die Funktion einfach ab, √(x+a) - (x+a) = 0 ist. Und durch Ausklammern erhalte ich √(x+a) * (1-√(x+a)) = 0. Wir haben jetzt hier ein Produkt, und ein Produkt wird null, wenn einer der Faktoren null wird, entweder der oder der. Das heißt, wir erhalten die beiden x-Koordinaten für die Nullstellen. x1=-a oder x2=1-a. Die schreibe ich hier mal hin: N1 (-a|0) und die Nullstelle N2(1-a|0). Zu dem y-Achsenschnittpunkt, hier setze ich in der Funktionsvorschrift für x null ein. Und wenn wir da oben schauen, Y, x null, erhalten wir √a - a. Was wir schon feststellen können ist, für negative a gibt es keine Y-Achsenschnittpunkte, da hier Wurzel aus a steht. Nachdem ich das alles gemacht habe, komme ich im Folgenden zu Extrema und Wendepunkten. Nachdem wir jetzt den Definitionsbereich, die Symmetrie, Ableitungen und Achsenschnittpunkte schon betrachtet haben, werde ich jetzt im Folgenden die Extrema mir anschauen. Für die Extrema muss notwendigerweise fa‘(xE)=0 sein. Ich übernehme die erste Ableitung, also 1 / (2√(xE+a) - 1 = 0. Das forme ich äquivalent um zu 2 * √(xE + a) = 1 und erhalte meine x-Koordinate ¼ - a. Um zu überprüfen, ob das jetzt wirklich ein Extremum ist, setze ich dieses ¼ - a in der zweiten Ableitung ein. Und das wäre minus eins durch, ich mache mal eine große Wurzel und vier mal davor, und jetzt kommt hier rein ¼ - a + a, das Ganze hoch drei. -a + a fliegt raus und wir bekommen hier raus -2, das ist ungleich null, also das was hier steht, wir haben also ein Extremum. Es ist kleiner null, das heißt wir haben einen Hochpunkt. Die x-Koordinaten des Hochpunktes haben wir hier, die hängen von dem Parameter a ab, also ¼ - a, die y-Koordinate bekommen wir, indem wir dieses ¼ - a in der Funktionsvorschrift einsetzen. Und ¼ - a + a = ¼ . √¼ = ½ , ½ - ¼ = ¼ . Du siehst also, die y-Koordinate des Hochpunktes hängt nicht von dem Parameter ab. Zu den Wendepunkten, da muss notwendigerweise die zweite Ableitung gleich null sein. Und da die zweite Ableitung- 1 / (4√(x+a)³) lautet sehen wir, die kann nie null werden, also haben wir keine Wendepunkte. Da wir das nun alles haben, können wir im Folgenden die Skizze anfertigen. Nachdem also die Punkte hier alle abgearbeitet sind, wir haben hier die Nullstellen, den y-Achsenabschnitt und den Hochpunkt jeweils in Abhängigkeit des Parameters a, werde ich jetzt die Funktion für verschiedene Parameter zeichnen. Ich habe hier unten das schon vorbereitet und auch das Koordinatensystem schon da. Ich fange an mit a = -1. Vorhin habe ich ja den Definitionsbereich angegeben, bei a = -1 startet die Funktion bei eins, das ist auch die erste Nullstelle, (1|0). Die zweite Nullstelle ist (2|0). Der Hochpunkt liegt bei (5/4|1/4). Einen y-Achsenabschnitt haben wir hier nicht, weil ja die Funktion für negative a, also Wurzel für negative a nicht definiert ist. Ich erhalte also diesen Funktionsverlauf und wie du siehst, geht die Funktion hier unten nach minus unendlich weg. Das Ganze mache ich jetzt auch für a = 0. Habe also die erste Nullstelle (0|0), die zweite Nullstelle (1|0), den Hochpunkt (1/4|1/4). Der y-Achsenabschnitt entspricht gerade der ersten Nullstelle. Ich zeichne die Funktion und auch hier geht die Funktion für x gegen plus unendlich nach minus unendlich. Und zu guter Letzt setze ich auch nochmal für a zwei ein. Aufgrund des Definitionsbereiches startet die Funktion dann hier, also die erste Nullstelle ist (-2|0), die zweite Nullstelle ist (-1|0). Der y-Achsenabschnitt ist (0|√2-2), das ist ungefähr -0,58, also ungefähr hier. Der Hochpunkt ist (-7/4|1/4), hier. Auch da zeichne ich die Funktion und erhalte diesen Verlauf. Was du hier erkennen kannst, ist dass die Funktionen alle sehr ähnlich aussehen. Ich habe ja vorhin bei den Hochpunkten schon erwähnt, dass die y-Koordinate sich nicht in Abhängigkeit von a verändert, das heißt die Funktionsgraphen werden entlang der x-Achse verschoben. Also zum Beispiel bei dem Funktionsgraphen von a = 2 ist es eine Verschiebung um zwei Längeneinheiten in negative x-Achsenrichtung. Ich fasse nochmal zusammen, was ich hier gemacht habe: Ich habe eine Kurvendiskussion mit einer Wurzelfunktion mit Parameter durchgeführt. Und die Ergebnisse die wir erhalten, hängen dann gegebenenfalls von dem Parameter ab. Und ich kann dann bei verschiedenen Parametern den Funktionsverlauf zeichnen, indem ich den Parameter in den Punkten einsetze. Ich hoffe, du konntest alles gut verstehen. Und freue mich über Fragen und Anregungen und bis zum nächsten Mal, dein Frank.
Scharen von Wurzelfunktionen – Kurvendiskussion Übung
-
Gib den Definitionsbereich der Wurzelfunktion an und untersuche die Funktion auf Symmetrie.
TippsBeachte: Die Wurzel ist nur für Zahlen größer oder gleich $0$ definiert.
Eine Funktion ist
- achsensymmetrisch zur y-Achse, wenn $f(-x)=f(x)$ ist, oder
- punktsymmetrisch zum Koordinatenursprung, wenn $f(-x)=-f(x)$ ist.
Der Definitionsbereich ist nicht symmetrisch.
LösungDer Definitionsbereich einer Funktion ist die Menge aller Werte, die für die Variable $x$ eingesetzt werden dürfen. Wir können uns also auch fragen, was nicht für $x$ eingesetzt werden darf.
Da eine Wurzel in der Funktion vorkommt, muss man sich klar machen, dass diese nur für Zahlen (Terme) größer oder gleich $0$ definiert ist: Dies führt zu der Ungleichung $x+a\ge 0$. Durch Subtraktion von $a$ erhält man $x\ge -a$.
Dann ist der Definitionsbereich der Funktionenschar gegeben durch:
$\mathbb{D}_{f_a}=\{x\in\mathbb{R}~:~x\ge -a\}$
Da der Definitionsbereich nur alle Zahlen größer oder gleich $-a$ umfasst, kann die Funktionenschar niemals symmetrisch sein.
-
Bestimme den Hochpunkt der Funktionsschar $f_a(x)=\sqrt{x+a}-(x+a)$.
TippsVerwende die Ableitung der Wurzelfunktion
$(\sqrt x)'=\frac1{2\sqrt x}$.
Bei Extrema muss für die 1. Ableitung $f'(x)=0$ gelten und für die 2. Ableitung an den ermittelten Stellen $f''(x_E) \neq 0$.
Wenn du zu einem gegebenen $x$-Wert den Funktionswert bestimmen möchtest, setzt du den $x$-Wert in die Funktionsgleichung ein.
LösungZunächst wollen wir die Funktion auf Nullstellen untersuchen. Es muss also gelten $f_a(x)=0$.
Das bedeutet $\sqrt{x+a}-(x+a)=0$. Durch Ausklammern von $\sqrt{x+a}$ erhält man
$\sqrt{x+a}\left(1-\sqrt{x+a}\right)=0$. Es muss also
- entweder $\sqrt{x+a}=0$ gelten (dies ist äquivalent zu $x=-a$)
- oder $1-\sqrt{x+a}=0$.
Die beiden Nullstellen sind dann $x_1=-a$ oder $x_2=1-a$. In welcher Weise du die Nullstellen nummerierst, ist natürlich nicht entscheidend.
Hier kann auch noch der y-Achsenabschnitt bestimmt werden. Hierfür wird $x=0$ in die Funktionsgleichung eingesetzt: $y=f_a(0)=\sqrt a-a$.
Kommen wir nun zu den Ableitungen. Die Ableitung der Wurzelfunktion ist
$(\sqrt x)'=\frac1{2\sqrt x}$.
Damit ist $f_a'(x)=\frac1{2\sqrt{x+a}}-1$. Die innere Ableitung ist dabei $1$.
Diese Ableitung kann als Potenz geschrieben und dann noch einmal abgeleitet werden:
$f_a'(x)=\frac12\left((x+a)^{-\frac12}\right)-1.$
Nun leiten wir ab:
$f_a''(x)=\frac12\cdot \left(-\frac12\right)\cdot(x+a)^{-\frac32}=-\frac1{4\sqrt{(x+a)^3}}$.
Hier ist schon zu sehen, dass die 2. Ableitung nie $0$ werden kann. Es kann also keine Wendepunkte geben.
Zur Untersuchung auf Extrema wird zunächst die Gleichung $f_a'(x)=0$ gelöst:
$\begin{array}{rclll} \frac1{2\sqrt{x+a}}-1&=&0&|&+1\\ \frac1{2\sqrt{x+a}}&=&1&|&\cdot\sqrt{x+a}\\ \frac12&=&\sqrt{x+a}&|&(~~)^2\\ \frac14&=&x+a&|&-a\\ \frac14-a&=&x \end{array}$
Um festzustellen, ob hier wirklich ein Extremum vorliegt und - wenn ja - welches, wird dieses Ergebnis in die 2. Ableitung eingesetzt:
$f_a''\left(\frac14-a\right)=-\frac1{4\sqrt{\frac14-a+a}}=-\frac12 < 0$.
Da die 2. Ableitung negativ ist, liegt ein Hochpunkt vor. Nun muss noch die y-Koordinate dieses Hochpunktes berechnet werden.
$f_a\left(\frac14-a\right)=\sqrt{\frac14-a+a}-(\frac14-a+a)=\sqrt{\frac14}-\frac14=\frac12-\frac14=\frac14$.
Damit ist der Hochpunkt $HP\left(\frac14-a\bigg\vert\frac14\right)$ gefunden.
-
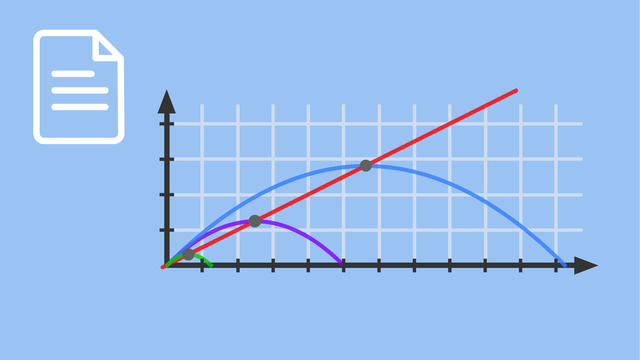
Entscheide, welcher Funktionsgraph zu welchem Parameter gehört.
TippsSchaue dir die gegebenen Informationen an: den Definitionsbereich, die Nullstellen sowie den Hochpunkt.
Setze jeweils den gegebenen Wert für den Parameter ein.
Zum Beispiel sind die Nullstellen für $a=0$ gegeben durch $x=0$ sowie $x=1$.
Für $a=2$ ist der Hochpunkt $HP\left(-1,75|0,25\right)$.
LösungWenn man zu einer Funktionenschar die Nullstellen, den y-Achsenabschnitt sowie die Extrema (und gegebenenfalls auch die Wendepunkte) berechnet hat, kann man diese für verschiedene Werte des Parameters $a$ in ein Koordinatensystem eintragen.
Übrigens: Diese Punkte (oder Stellen) müssen nicht von dem Parameter abhängen.
Wenn man dann die so erhaltenen Punkte miteinander verbindet, erhält man die Graphen von verschiedenen Funktionen der Funktionenschar.
Um zu erkennen, welcher Graph zu welchem Parameter gehört, kann man sich die Punkte anschauen. In diesem Beispiel genügt bereits ein Blick auf den Definitionsbereich. Die Graphen müssen in dieser Reihenfolge mit den Parametern versehen werden:
- $a=0$
- $a=-1$
- $a=2$
- $a=-3$
- $a=1$
-
Leite die Funktionenschar zweimal ab und gib die Achsenabschnitte an.
TippsDie Nullstellen erhältst du durch Lösen der Gleichung $f_a(x)=0$.
Den y-Achsenabschnitt erhältst du durch Einsetzen von $x=0$ in die Funktionsgleichung $y=f_a(0)$.
Verwende die Kettenregel
$(f(g(x)))'=f'(g(x))\cdot g'(x)$
sowie
$(\sqrt{x})'=\frac1{2\sqrt{x}}$.
LösungAchsenabschnitte
- Damit $f_a(x)=0$ ist, muss der Term unter der Wurzel $x^2+a^2=0$ sein. Da $a>0$ nach Voraussetzung gilt, kann die Summe der beiden Quadrate nie $0$ sein. Damit kann es keine Nullstellen geben.
- Zur Bestimmung des y-Achsenabschnittes wird $x=0$ in die Funktionsgleichung eingesetzt. So erhält man $f_a(0)=\sqrt{0^2+a^2}=a$.
Es ist $f_a(x)=\sqrt{x^2+a^2}$. Damit lässt sich $f_a'(x)$ wie folgt mit Hilfe der Kettenregel, $(f(g(x)))'=f'(g(x))\cdot g'(x)$, sowie $(\sqrt{x})'=\frac1{2\sqrt{x}}$ berechnen:
$f_a'(x)=\left(\sqrt{x^2+a^2}\right)'=\frac1{2\sqrt{x^2+a^2}}\cdot 2x=\frac x{\sqrt{x^2+a^2}}$.
Nun kann die zweite Ableitung berechnet werden:
$\left(\frac x{\sqrt{x^2+a^2}}\right)'=\frac{\sqrt{x^2+a^2}-\frac{x^2}{\sqrt{x^2+a^2}}}{\sqrt{x^2+a^2}^2}=\frac{a^2}{\sqrt{x^2+a^2}^3}$.
Dabei wurde die Quotientenregel verwendet.
-
Nenne die verschiedenen Bestandteile und Eigenschaften einer Kurvendiskussion.
TippsMan kann sicher eine Umkehrfunktion bestimmen, sofern es eine gibt.
Die Funktion $f_a(x)=\sqrt{x+a}-(x+a)$ besitzt übrigens keine Umkehrfunktion.
Der Punkt $(0|4)$ kann ein y-Achsenabschnitt sein, der Punkt $(4|0)$ nicht. Dort kann allerdings eine Nullstelle liegen.
LösungDie einzelnen Punkte einer Kurvendiskussion sind:
- Bestimmung des Definitionsbereichs
- Untersuchung der Funktion auf Symmetrie
- Ermittlung der ersten drei Ableitungen (manchmal genügen sogar schon die ersten beiden)
- Bestimmung der Nullstellen und des y-Achsenabschnitts
- Bestimmung der Extrema der Funktion
- Zeichnen einer Skizze in ein Koordinatensystem mithilfe der Ergebnisse aus den vorigen Schritten
-
Untersuche die Funktionenschar auf Extrema.
TippsDie erste Ableitung ist ein Bruch. Ein Bruch wird nur $0$, wenn der Zähler $0$ wird.
Setze die Lösung der Gleichung $f_a'(x)=0$ in die zweite Ableitung ein: $f''(x_E)$
Ist diese größer (kleiner) $0$, liegt ein Tiefpunkt (Hochpunkt) vor.
LösungFür Extrema muss $f_a'(x)=0$ sein, also
$\frac x{\sqrt{x^2+a^2}}=0$.
Dies ist äquivalent zu $x=0$.
Einsetzen von $x=0$ in die zweite Ableitung führt zu
$f_a''(0)=\frac{a^2}{\sqrt{0^2+a^2}^3}=\frac{a^2}{a^3}=\frac1a$
Da nach Voraussetzung $a>0$ ist, führt dies zu einem Tiefpunkt.
Die y-Koordinate des Tiefpunktes ist $f_a(0)=\sqrt{0^2+a^2}=a$.
Somit ist $TP(0|a)$ der Tiefpunkt der Funktionenschar.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9.957
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.313
Lernvideos
38.641
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









In der Lösung bei den multiple choice steht dass die Auswahl mit x kleiner gleich a falsch ist und in der Lösung soll sie richtig sein , warum?