Schar von Winkelfunktionen – Kurvendiskussion


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Schar von Winkelfunktionen – Kurvendiskussion
Wenn Du bereits eine Kurvendiskussion mit einer trigonometrischen Funktion durchgeführt hast, wird es Dich sicher interessieren, wie sich ein Parameter auf die Kurvendiskussion und damit auch auf den Funktionsgraphen auswirkt. Ein Parameter kann zu Verschiebungen entlang der x-Achse oder der y-Achse führen; er kann aber auch dazu führen, dass sich die Frequenz oder die Amplitude der Funktion verändern. All dies kannst Du bereits erkennen, wenn Du eine Kurvendiskussion durchführst, da die Nullstellen, Extrema und auch Wendepunkte von dem Parameter abhängen. Natürlich freue ich mich über Fragen und Anregungen von Dir. Bis zum nächsten Mal, Dein Frank.
Transkript Schar von Winkelfunktionen – Kurvendiskussion
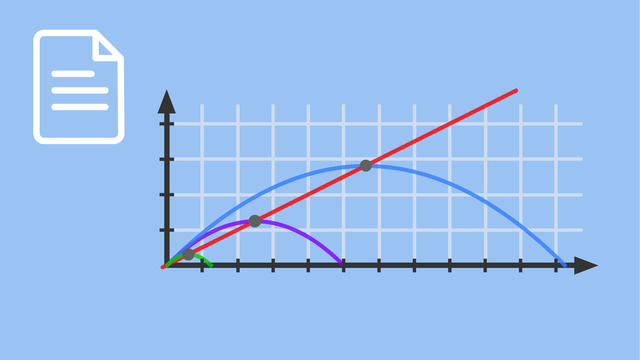
Hallo. Mein Name ist Frank. In diesem Video, werde ich mit Dir eine Kurvendiskussion mit einer trigonometrischen Funktion durchführen. Die trigonometrische Funktion hat hier ein Parameter a, den ich größer Null gewählt habe und ich schränke die Funktion auf das Intervall -Pi bis Pi ein, was jetzt aufgrund der Periodizität keine Einschränkung ist, aber es erleichtert mir im Folgenden die Rechnung. Und zunächst einmal, möchte ich Dir zeigen für den Parameter a = 1, wie der Faktor zwei und die Addition von eins den Verlauf der Sinusfunktion verändert. Dafür siehst Du hier links den Verlauf der Sinusfunktion und ich beginne mit dem Faktor zwei. Wenn ich die Funktion mit zwei multipliziere heißt das, die Nullstellen bleiben fest und die Funktion wird sowohl nach oben als nach unten um eine Längeneinheit gestreckt. Wenn der Faktor kleiner als eins wäre, würde die Funktion so zusammengestaucht werden. Das Addieren von eins führt dazu, dass der komplette Funktionsgraph um eins nach oben gehoben wird. Das siehst Du hier. Nun haben wir schon mal den Verlauf der Funktion für a = 1, also 2 sin(x) + 1, da eine Skizze stehen. Ich fange an mit den Ableitungen. Die erste Ableitung ist nach der Kettenregel, die zwei bleibt einfach mal stehen, die Ableitung von Sinus x ist Cosinus x, die innere Funktion schreibe ich einfach ab und mal ableiten der inneren Funktion, die schreibe ich hier hin. Und ebenso bekomme ich die zweite Ableitung 2a lasse ich stehen, die Ableitung von Cosinus x: minus Sinus und durch die Ableitung der inneren Funktion bekomme ich noch einen Faktor a rein, also habe ich insgesamt -2a²sin (ax). Und dann die dritte Ableitung auch wieder so. Die lautet dann -2 * a³, Ableitung von Sinus ist Cosinus, a x. Gut. Dann kann ich mich im Folgenden den Achsenschnittpunkten widmen. So, nun geht es weiter mit den Achsenschnittpunkten. Zunächst einmal schaue ich mir die X-Achsenschnittpunkte, also die Nullstellen an. fa(x) = 0. Ich erhalte also die Gleichung: 2 * sin (a * x) + 1 = 0. Und wenn ich jetzt die eins da rüberbringe, durch zwei teile erhalte ich also: sin (a * x) = - ½. Eine Lösung davon bekommst Du mit dem Taschenrechner. Also am Taschenrechner sin-1 eingeben und dann erhältst Du die Lösung a * x = - π/6. Und das ist jetzt nur eine der Basislösungen, die andere wäre gegeben durch a * x und deswegen habe hier den Index eins hinzugefügt. a * x2 = - 5π/6. Das heißt, wir bekommen zwei Nullstellen raus: x1 = -π/6a oder x2 = - 5π/6a. Gut. Die Achsenschnittpunkte haben wir jetzt, also die X-Achsenschnittpunkte, die Nullstellen bei - π/6a entsprechen der Y-Koordinate Null, deswegen heißt die Nullstelle Nullstelle und die zweite bei - 5π/6a entsprechend wieder die Y-Koordinate Null. Den Y-Achsenabschnitt bekomme ich wie immer dadurch, dass ich x = 0 einsetze, a * 0 = 0, Sinus von Null ist Null, 2 * 0 + 1 = 1. Du kannst hier schon erkennen, der Y-Achsenabschnitt ist unabhängig von dem Parameter a. Und hier in der Skizze siehst Du dann schon oder kannst es sehen, bei der Funktion für a = 1, die Nullstelle 1 bei -π/6, die Nullstelle 2 bei -5π/6. Dann mache ich weiter mit den Extrema. Notwendig für die Extrema, erste Ableitung der Funktion muss Null sein. Die erste Ableitung lautet 2 * a * cos(a * xE) = 0. Da dieser Faktor nie Null wird, muss cos(a * xE) Null werden, also brauchen wir die Nullstellen von Cosinus und vielleicht weißt Du die noch auswendig, die Nullstellen von Cosinus sind π/2 plus ein ganzzahlige Vielfache von π. Also hätten wir a * xE1 = - π/2, auf unserem Intervall hier. Und a * xE2 = π/2. Und wenn wir durch a teilen bekommen wir also xE1 = - π/2a oder xE2 = π/2a. Und jetzt schauen wir noch, ob das wirklich ein Extremum ist, also das hinreichende Kriterium f’'a(-π/2a) = hier ist die zweite Ableitung, also -2 * a² * sin (a * (-π/2a)). Dieses a kürze ich raus, also steht da sin(-π/2). Und sin(-π/2) = -1. Also hier kommt 2a² raus. Das ist größer Null, also haben wir einen Tiefpunkt. Und genauso f’'a(π/2a) = ich kürze das jetzt mal ab, da kommt dann raus -2a², das ist kleiner Null, das heißt, wir hätten da einen Hochpunkt. Gut. Die Extrema habe ich jetzt hier hingeschrieben. Also wir haben einen Tiefpunkt gefunden bei -π/2a. Und wenn ich -π/2a hier einsetze bekomme ich hier sin(-π/2), das ist -1. 2 * -1 +1 = -1. Und einen Hochpunkt bei π/2a. Und wenn ich π/2a hier einsetze bekomme ich sin (π/2) = 1. 2 * 1 + 1 = 3. Und für a = 1 kannst Du den Hochpunkt und den Tiefpunkt hier an der Skizze sehen. Ich mache weiter mit den Wendepunkten. Notwendig für die Wendepunkte: Zweite Ableitung muss Null sein. Die zweite Ableitung siehst Du hier. Also -2 * a² * sin(a * xW) = 0. Also dieser Term wird nicht Null. sin(a *xW) = 0. Und wenn Du die Nullstellen von Sinus noch weißt, weißt Du, dass entweder a * xW1 = -π ist oder a * xW2 = 0 oder a * xW3 = π. Das sind die drei Sinus Nullstellen auf unserem Intervall. Wenn wir durch a teilen bekommen wir xW1 = -π/a. xW2 = 0 / a, also null. Und xW3 = π/a. Das hinreichende Kriterium führe ich exemplarisch für einen dieser Werte durch. Also die dritte Ableitung an der Stelle -π/a ist gleich. Dritte Ableitung siehst Du hier, also -2 * a³ * cos(a * (-π/a)). A kürze ich raus, also cos(-π) und cos(-π) = 1, also komm 2 * a³ raus. Das ist ungleich Null, wir haben also eine Wendestelle, einen Wendepunkt gefunden, wie gesagt bei Null und π/a läuft das gleich. So, die Wendepunkte habe ich hier angeschrieben. Die x-Koordinaten haben wir gerade berechnet: -π/a, 0 und π/a. Und wenn ich zum Beispiel -π/a hier einsetze, steht dann, das a kürze ich raus, -π, sin(-π) = 0, also 1, analog dazu auch hier. Die Wendepunkte haben wir dann hier stehen. Und auch hier wieder, wenn Du a = 1 einsetzt, kannst Du die Wendepunkte bei -π, bei 0 und bei π auch schon in dem Funktionsgraphen sehen. Nun haben wir hier noch einen Parameter a. Und ich schaue mir jetzt noch an, wie sich der Verlauf der Funktion verändert, wenn ich verschiedene Werte für a nehme. Und dann fange ich einfach mal an mit a = 0,5; das siehst Du da. Und wie Du da feststellen kannst, durch den Faktor 0,5 wird die Funktion so auseinandergezogen. Das heißt also diese Schwingungen hier, das nennt man die Amplitude, bleibt gleich. Aber hier, die Frequenz, wird geringer. Oder anders ausgedrückt: Die Periode der Funktion verändert sich von 2π zu 4π. Und wenn ich für a zwei einsetze, das siehst Du jetzt auch hier, dann kannst Du erkennen, die Funktion wird so zusammengeschoben, auch da, die Amplitude bleibt gleich, aber die Frequenz wird höher. Oder anders ausgedrückt: Die Periode wird kleiner, in dem Fall π. So, dann fasse ich noch einmal zusammen, was ich in diesem Video gemacht habe: Ich habe eine Kurvendiskussion mit einer trigonometrischen Funktion, mit einem Scharparameter a durchgeführt. Die Ergebnisse, die wir hier erhalten hängen vom Parameter a ab und je nach Wahl des Parameters bekommen wir verschiedene Verläufe. Und wenn das a hier drin steht, wie in dem Beispiel, verändert sich die Frequenz. So, dann danke ich Dir, für Deine Aufmerksamkeit, hoffe, dass Du alles gut verstehen konntest und freue mich wie immer über Fragen und Anregungen, dein Frank. Bis zum nächsten Mal.
Schar von Winkelfunktionen – Kurvendiskussion Übung
-
Berechne die Nullstellen der Funktion.
TippsBeachte, dass der Taschenrechner auf „R“ oder „RAD“ für Bogenmaß eingestellt sein muss.
Der Taschenrechner gibt durch Umkehrung der Sinus-Funktion einen Wert aus. Es existieren weitere Lösungen der entsprechenden Gleichung auf Grund der Periodizität der Sinus-Funktion.
LösungEs muss die Gleichung $f_a(x)=0$ gelöst werden.
$\begin{aligned} &&2 \cdot \sin(ax)+1&=0&~|~&-1\\ &\Leftrightarrow&2 \cdot \sin(ax)&=-1&~|~&:2\\ &\Leftrightarrow&\sin(ax)&=-\frac12. \end{aligned}$
Die Umkehrung der Sinusfunktion mit dem Taschenrechner führt zu dem Ergebnis:
$ax=-\frac{\pi}6$.
Dabei ist zu beachten, dass der Taschenrechner auf „R“ oder „RAD“ für Bogenmaß eingestellt sein muss.
Auf Grund der Periodizität liegen auf dem oben angegebenen Intervall $[-\pi;\pi]$ zwei Nullstellen für $a=1$:
$x_1=-\frac{\pi}6$ und $x_2=-\frac{5\pi}6$.
Es existieren also 2 Nullstellen $N_1\left(-\frac{\pi}6|0\right)$ sowie $N_2\left(-\frac{5\pi}6|0\right)$.
-
Gib die Extrema und Wendepunkte der Funktion an.
TippsEs existieren
- ein Tiefpunkt,
- ein Hochpunkt und
- drei Wendepunkte.
Für Extrema, Tiefpunkte oder Hochpunkte, muss die Gleichung $\large{f_a'(x)=0}$ gelöst werden.
Für Wendepunkte muss die Gleichung $\large{f_a''(x)=0}$ gelöst werden.
Die Ableitung von $\large{\sin(ax)}$ ist mit der Kettenregel
$\large{(\sin(ax))'=a\cos(ax)}$.
LösungHier ist der Graph der Funktion für $a=1$ zu sehen.
Zunächst werden die ersten drei Ableitungen der Funktion benötigt:
$\begin{aligned} f(x)&=2\sin(ax)+1\\ f'(x)&=2a\cos(ax)\\ f''(x)&=-2a^2\sin(ax)\\ f'''(x)&=-2a^3\cos(ax). \end{aligned}$
Dabei wurde die Kettenregel verwendet. Der Faktor $a$ vor dem $x$ wird als innere Ableitung immer multipliziert.
Extrema $\rightarrow$ (n) $f_a'(x_E)=0$ und (h) $f_a''(x_E)\neq0$
$\begin{aligned} &&2a\cos(ax)&=0~|~:(2a)\\ &\Leftrightarrow&\cos(ax)&=0. \end{aligned}$
Da die Nullstellen von $\cos(x)$ auf dem Intervall $[-\pi;\pi]$ durch $x_1=-\frac{\pi}2$ und $x_2=\frac{\pi}2$ gegeben sind, gilt
$x_{E1}=-\frac{\pi}{2a}$ und $x_{E2}=\frac{\pi}{2a}$.
Ob wirklich Extrema vorliegen, kann man überprüfen, indem man die jeweilige x-Koordinate in der 2. Ableitung einsetzt.
- $f_a''\left(-\frac{\pi}{2a}\right)=-2a^2\sin\left(-a\frac{\pi}{2a}\right)=2a^2>0$. Also liegt ein Tiefpunkt vor. Die y-Koordinate ist $y=2\sin\left(-a\frac{\pi}{2a}\right)+1=-2+1=-1$. Somit ist der Tiefpunkt $TP\left(-\frac{\pi}{2a}|{-}1\right)$.
- $f_a''\left(\frac{\pi}{2a}\right)=-2a^2\sin\left(a\frac{\pi}{2a}\right)=-2a^2<0$. Also liegt ein Hochpunkt vor. Die y-Koordinate ist $y=2\sin\left(a\frac{\pi}{2a}\right)+1=2+1=3$. Somit ist der Hochpunkt $HP\left(\frac{\pi}{2a}|3\right)$.
$\begin{aligned} &&-2a^2\sin(ax)&=0~|~:(-2a^2)\\ &\Leftrightarrow&\sin(ax)&=0. \end{aligned}$
Die Nullstellen von $\sin(x)$ sind die ganzzahligen Vielfachen von $\pi$, also gibt es auf dem Intervall $[-\pi;\pi]$ die Nullstellen der 2. Ableitung $x_{W_1}=-\frac{\pi}a$, $x_{W_2}=0$ und $x_{W_3}=\frac{\pi}a$.
Ob es sich tatsächlich um Wendepunkte handelt, kann man überprüfen, indem man jeweils die x-Koordinate in der 3. Ableitung einsetzt.
- $f_a'''\left(-\frac{\pi}a\right)=-2a^3\cos\left(-a\cdot\frac{\pi}a\right)=-2a^3\cos\left(-\pi\right)=2a^3\neq0$, also liegt ein Wendepunkt vor. Die y-Koordinate ist $y=2\sin\left(-a\frac{\pi}a\right)+1=0+1=1$, also $WP_1\left(-\frac{\pi}a|1\right)$.
- $f_a'''\left(0\right)=-2a^3\cos\left(0\right)=-2a^3\neq0$, also liegt ein Wendepunkt vor. Die y-Koordinate ist $y=2\sin(0)+1=0+1=1$, also $WP_2\left(0|1\right)$.
- $f_a'''\left(\frac{\pi}a\right)=-2a^3\cos\left(a\cdot\frac{\pi}a\right)=-2a^3\cos\left(\pi\right)=2a^3\neq0$, also liegt ein Wendepunkt vor. Die y-Koordinate ist $y=2\sin\left(a\frac{\pi}a\right)+1=0+1=1$, also $WP_3\left(\frac{\pi}a|1\right)$.
-
Bestimme die Ableitungen der Funktion $g_a(x)=\frac12\cos(x+a)+2; ~x\in\left[-\pi;\pi\right]$.
TippsDie Ableitungen der trigonometrischen Funktionen sind
- $\large{(\sin(x))'=\cos(x)}$ und
- $\large{(\cos(x))'=-\sin(x)}$.
Die Kettenregel lautet $\large{(f(g(x)))'=f'(g(x))\cdot g'(x)}$.
LösungIm folgenden wird
- $(\sin(x))'=\cos(x)$,
- $(\cos(x))'=-\sin(x)$ und
- die Kettenregel $(f(g(x)))'=f'(g(x))\cdot g'(x)$
$\begin{align*} g_a(x)&=\frac12\cos(x+a)+2\\ g_a'(x)&=-\frac12\sin(x+a)\\ g_a''(x)&=-\frac12\cos(x+a)\\ g_a'''(x)&=\frac12\sin(x+a). \end{align*}$
-
Untersuche die Funktion auf Nullstellen, Extrema und Wendepunkte und gib diese für $a=2$ an.
TippsDie ersten drei Ableitungen sind:
$\begin{aligned} g_a'(x)&=-\frac12\sin(x+a)\\ g_a''(x)&=-\frac12\cos(x+a)\\ g_a'''(x)&=\frac12\sin(x+a). \end{aligned}$
Für Nullstellen, Extrema und Wendepunkte müssen Gleichungen gelöst werden:
- Nullstellen: $g_a(x)=0$,
- Extrema: $g_a'(x)=0$ und
- Wendepunkte: $g_a''(x)=0$.
Sowohl bei Extrema und Wendepunkten muss ein hinreichendes Kriterium überprüft werden:
- Extrema: $g_a''(x_E)\neq0$ und
- Wendepunkte: $g_a'''(x_W)\neq0$.
Ist die 2. Ableitung an der Stelle $x_E$ ungleich $0$, so ist sie
- entweder größer als $0$, dann liegt ein Tiefpunt vor,
- oder sie ist kleiner als $0$, dann liegt ein Hochpunkt vor.
LösungDas Bild zeigt den Graphen für $a=2$.
Die ersten drei Ableitungen sind:
$\begin{aligned} g_a'(x)&=-\frac12\sin(x+a)\\ g_a''(x)&=-\frac12\cos(x+a)\\ g_a'''(x)&=\frac12\sin(x+a). \end{aligned}$
- Nullstellen $\rightarrow g_a(x)=0$
Da der Wertebereich von $\cos(x)$ durch $[-1;1]$ gegeben ist und $-4$ nicht in diesem Wertebereich liegt, gibt es keine Nullstellen.
Der Wertebereich der Funktionenschar $g_a(x)$ ist, unabhängig von dem Scharparameter, $\mathbb{W}_{g_a}=[1,5;2,5]$. Daran ist bereits zu erkennen, dass die Funktion keine Nullstellen haben kann.
- Extrema $\rightarrow$ (n) $g_a'(x_E)=0$ und (h) $g_a''(x_E)\neq0$
Die Nullstellen von $\sin(x)$ sind die ganzzahligen Vielfachen von $\pi$. Also gilt $x=k\cdot \pi-a,~k\in\mathbb{Z}$. Somit gibt es zwei mögliche Extremstellen auf dem Intervall $[-\pi;\pi]$ für $a=2$, diese sind $x_{E_1}=-2$ und $x_{E_2}=\pi-2\approx 1,14$.
Ob dort tatsächlich Extrema vorliegen, kann man überprüfen, indem man die jeweilige x-Koordinate in der 2. Ableitung einsetzt.
- $g_a''(\pi-2)=-\frac12\cos(\pi-2+2)=\frac12>0$. Es liegt also ein Tiefpunkt vor mit der y-Koordinate $y=\frac12\cos(\pi-2+2)+2=1,5$. Somit ist $TP(1,14|1,5)$ ein Tiefpunkt.
- $g_a''(-2)=-\frac12\cos(-2+2)=-\frac12<0$. Es liegt also ein Hochpunkt vor mit der y-Koordinate $y=\frac12\cos(-2+2)+2=2,5$. Somit liegt bei $HP(-2|2,5)$ ein Hochpunkt vor.
- Wendepunkte $\rightarrow$ (n) $g_a''(x_W)=0$ und (h) $g_a'''(x_W)\neq0$
Da die Nullstellen von $\cos(x)$ durch $x=\frac{2k+1}2\cdot \pi,~k\in\mathbb{Z}$ gegeben sind, liegen für $a=2$ zwei mögliche Wendestellen auf dem Intervall $[-\pi;\pi]$. Diese sind $x_{W_1}=\frac{3\pi}2-2\approx2,71$ und $x_{W_2}=\frac{\pi}2-2\approx -0,43$.
Ob dort tatsächlich Wendepunkte vorliegen, kann man überprüfen, indem man die jeweilige x-Koordinate in der 3. Ableitung einsetzt.
- $g_a'''\left(\frac{3\pi}2-2\right)=\frac12\sin\left(\frac{3\pi}2-2+2\right)=\frac12\sin\left(\frac{3\pi}2\right)=-\frac12\neq0$. Also liegt ein Wendepunkt vor. Die y-Koordinate dieses Wendepunktes ist $y=\frac12\cos\left(\frac{3\pi}2-2+2\right)+2=\frac12\cos\left(\frac{3\pi}2\right)+2=2$. Damit lautet der Wendepunkt $WP_1(2,71|2)$.
- $g_a'''\left(\frac{\pi}2-2\right)=\frac12\sin\left(\frac{\pi}2-2+2\right)=\frac12\sin\left(\frac{\pi}2\right)=\frac12\neq0$. Also liegt ein Wendepunkt vor. Die y-Koordinate dieses Wendepunktes ist $y=\frac12\cos\left(\frac{\pi}2-2+2\right)+2=\frac12\cos\left(\frac{\pi}2\right)+2=2$. Damit lautet der Wendepunkt $WP_2(-0,43|2)$.
-
Beschreibe die Streckung und Verschiebung der Sinusfunktion.
TippsWird zu dem Funktionswert eine positive Zahl addiert oder davon subtrahiert, so erfolgt eine Verschiebung entlang der $y$-Achse.
Die Multiplikation mit dem Faktor $2$ bewirkt eine Veränderung des Wertebereiches von $\large{[-1;1]}$ für $\sin(x)$ zu $\large{[-2;2]}$ für $2\sin(x)$.
LösungZunächst wird die Auswirkung des Faktors $2$ auf die Sinusfunktion betrachtet. Dies ist gut an dem Wertebereich zu erkennen. Dieser ist $[-1;1]$ für $\sin(x)$. Durch die Multiplikation mit $2$ wird jeder Funktionswert mit $2$ multipliziert, also ist $[-2;2]$ der Wertebereich von $2\sin(x)$. Es handelt sich also um eine Streckung um den Faktor $2$.
Allgemein bedeutet ein positiver Faktor größer als $1$ eine Streckung und ein Faktor kleiner als $1$ eine Stauchung. Ist der Faktor negativ, wird die Funktion an der x-Achse gespiegelt.
Die Addition von $1$ zu dem Funktionswert führt zu einer Verschiebung um $1$ Einheit nach oben.
Somit ist der Wertebereich der Funktion $f(x)=2\sin(x)+1$ gegeben durch $\mathbb{W}_f=[-1;3]$.
-
Bestimme die Lösungen der trigonometrischen Gleichung auf dem Intervall $[-\pi;\pi]$.
TippsEs gilt
- $\large{\cos(x)=1\Leftrightarrow x=2k\cdot\pi~;~k\in\mathbb{Z}}$ und
- $\large{\cos(x)=-1\Leftrightarrow x=(2k+1)\cdot\pi~;~k\in\mathbb{Z}}$.
Die Nullstellen von $\large{\cos(x)}$ sind gegeben durch $\large{x=\frac{2k+1}2\cdot \pi,~k\in\mathbb{Z}}$.
Achte darauf, dass dein Taschenrechner auf „R“ oder „RAD“ für Bogenmaß eingestellt ist.
LösungEin Produkt wird $0$, wenn einer der Faktoren $0$ ist. Also gilt hier
- entweder ist $\sin(x)-1=0$, was äquivalent ist zu $\sin(x)=1$,
- oder $\cos(x)-a=0$, dies ist äquivalent zu $\cos(x)=a$.
Die Gleichung $\cos(x)=a$ ist nur lösbar für $a\in[-1;1]$. Hier muss eine Falluntersuchung durchgeführt werden
- Sei $a=1$, so führt dies zu der Lösung $x_{2_1}=0$,
- sei $a=-1$, so führt dies zu den Lösungen $x_{2_2}=-\pi$ und $x_{2_3}=\pi$ und
- sei $a=0$, so führt dies zu der Lösung $x_{2_4}=-\frac{\pi}2$. Die andere Stelle, an welcher der Kosinus den Wert $0$ annimmt, ist $x_{2_5}=\frac{\pi}2$.
- Für alle $a\in (0;1)$ gibt der Taschenrechner einen Wert zwischen $0$ und $\frac{\pi}2$ aus. Dieser sei $x_{2}$. Dann existiert eine weitere Stelle, und zwar $x_3=\pi-x_2$.
- Für alle $a\in (-1;0)$ gibt der Taschenrechner einen Wert zwischen $-\frac{\pi}2$ und $0$ aus. Dieser sei $x_2$. Dann existiert eine weitere Stelle, und zwar $x_3=x_2-\pi$.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9.892
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.669
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?









Hallo Katja.
Da eine Lösung (mit dem Taschenrechner) - pi/6 ist, erhältst Du die zweite Lösung auf [-pi;0], indem Du auf den rechten Rand, also -pi, pi/6 addierst (-> Basislösungen) und das ist gerade -5 pi/6.
Ich hoffe, das war verständlich.
Wie kommt man bei den Nullstellen auf die 5/6tel?