Gleichungen mit Sinus, Cosinus und Tangens
geometrische Gleichungen, sin x, cos x, tan x, Sinusfunktion, Cosinusfunktion
Inhaltsverzeichnis zum Thema
- Was ist eine trigonometrische Gleichung?
- Lösen von trigonometrischen Gleichungen
- $\sin(x)=c$
- $\cos(x)=c$
- $\tan(x)=c$
Was ist eine trigonometrische Gleichung?
Eine trigonometrische Gleichung ist eine Gleichung, in welcher mindestens eine trigonometrische Funktion Sinus, Cosinus oder Tangens vorkommt.
Um solche Gleichungen zu lösen, benötigst du einen Taschenrechner. Achte darauf, dass dieser auf DEG für degree, also Winkelmaß, eingestellt ist.
Lösen von trigonometrischen Gleichungen
$\sin(x)=c$
Eine trigonometrische Gleichung ist zum Beispiel durch $\sin(x)=0,5$ gegeben. Es werden also alle Werte für $x$ gesucht, für welche $f(x)=\sin(x)=0,5$ ist. Schaue dir den Graphen der Funktion $f(x)=\sin(x)$ an.
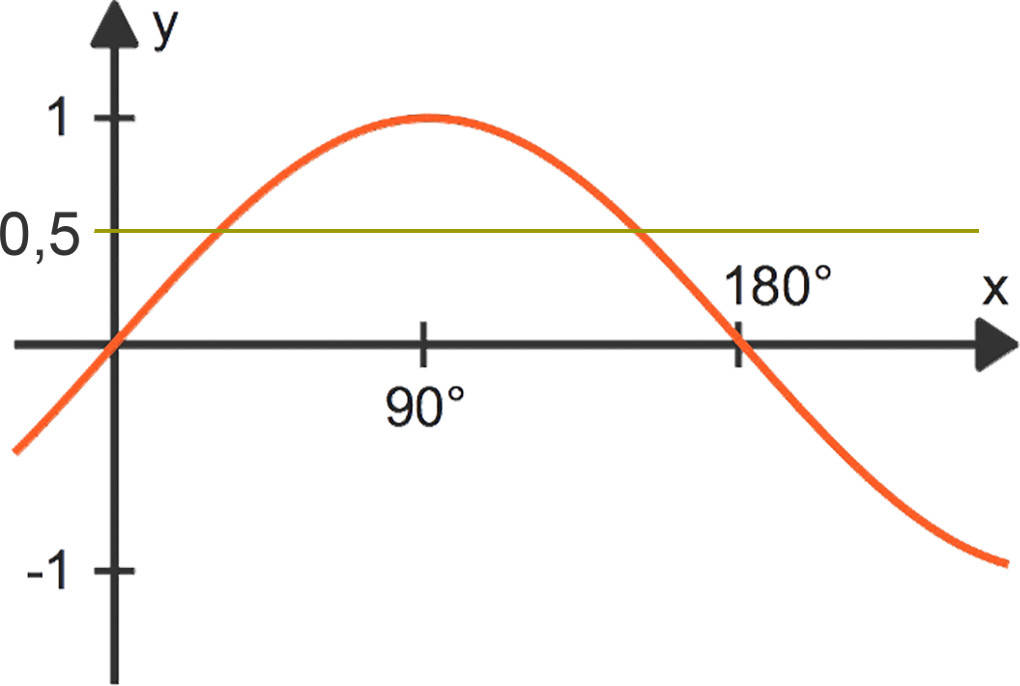
- Um eine Lösung der obigen Gleichung zu erhalten, verwendest du auf dem Taschenrechner die Umkehrfunktion von $\sin(x)$, den Arkussinus $\sin^{-1}$ oder $\arcsin$.
- Eine Lösung der Gleichung ist dann $x_1=sin^{-1}(0,5)=30^\circ$.
- Der Taschenrechner gibt für Gleichungen der Form $\sin(x)=c$, mit $c\in[-1;1]$, immer Werte zwischen $-90^\circ$ und $90^\circ$ aus.
- Wie du an dem Funktionsgraphen erkennen kannst, gibt es noch eine weitere Lösung. Diese erhältst du, indem du von $180^\circ$ die vom Taschenrechner ausgegebene Lösung, also $30^\circ$, subtrahierst: $x_2=180^\circ-30^\circ=150^\circ$.
- Das so erhaltene Lösungspaar $x_1=30^\circ$ sowie $x_2=150^\circ$ wird als Basislösung bezeichnet.
- Auf Grund der $360^\circ$-Periodizität der Sinusfunktion sind alle Lösungen der Gleichung dann gegeben durch:
$\quad~~~x_1^{(k)}=30^\circ+k\cdot 360^\circ$, $k\in\mathbb{Z}$ sowie
$\quad~~~x_2^{(k)}=150^\circ+k\cdot 360^\circ$, $k\in\mathbb{Z}$.
Ähnlich erhältst du alle Lösungen, wenn auf einer Seite der Gleichung eine negative Zahl steht: $\sin(x)=-0,5$.
- Dann ist $x_1=\sin^{-1}(-0,5)=-30^\circ$.
- Die andere Basislösung ist dann $x_2=-180^\circ+30^\circ=-150^\circ$.
- Auch hier erhältst du die Lösungsgesamtheit mit Hilfe der Periodizität.
$\quad~~~x_1^{(k)}= -30^\circ-k\cdot 360^\circ$, $k\in\mathbb{Z}$ sowie
$\quad~~~x_2^{(k)}= -150^\circ-k\cdot 360^\circ$, $k\in\mathbb{Z}$.
$\cos(x)=c$
- Der Taschenrechner gibt für Gleichungen der Form $\cos(x)=c$, mit $c\in[-1;1]$, immer Werte zwischen $0^\circ$ und $180^\circ$ aus.
- Die jeweils andere Basislösung erhältst du durch Vertauschen des Vorzeichens.
- Auch hier kannst du die Lösungsgesamtheit unter Verwendung der Periodizität der Cosinusfunktion angeben.
Beispiel: $\cos(x)=\frac1{\sqrt2}$
Dann ist
$x_1=\cos^{-1}\left(\frac1{\sqrt2}\right)=45^\circ$.
Nun ist $x_2=-45^\circ$ und
$\quad~~~x_1^{(k)}=45^\circ+k\cdot 360^\circ$, $k\in\mathbb{Z}$ sowie
$\quad~~~x_2^{(k)}=-45^\circ+k\cdot 360^\circ$, $k\in\mathbb{Z}$.
$\tan(x)=c$
- Die Tangensfunktion ist $180^\circ$-periodisch.
- Der Taschenrechner gibt einen Winkel zwischen $-90^\circ$ sowie $90^\circ$ aus. (Beachte, dass der Tangens weder für $90^\circ$ noch für $-90^\circ$ definiert ist.)
Beispiel: $\tan(x)=1$
- Die Taschenrechnerlösung ist $x=\tan^{-1}(1)=45^\circ$.
- Die Lösungsgesamtheit ist dann gegeben durch
$\quad~~~x^{(k)}=45^\circ+k\cdot 180^\circ$, $k\in\mathbb{Z}$.
Trigonometrische Gleichungen mit zwei Winkelfunktionen und demselben Argument
Wie kannst du trigonometrische Gleichung lösen, in der zwei verschiedene Winkelfunktionen mit demselben Argument vorkommen?
$(\cos(x))^3-2\cos(x)\cdot \sin^2(x)=0$
- Zuerst klammerst du $\cos(x)$ aus.
$\quad~~~\cos(x)\left(\cos^2(x)-2 \sin^2(x)\right)=0$
- Ein Produkt wird $0$, wenn einer der Faktoren $0$ wird. Also ist entweder $\cos(x)=0$ oder $\cos^2(x)-2 \sin^2(x)=0$.
- Die Nullstellen von $\cos(x)$ sind $x=(2k+1)\cdot 90^\circ$, $k\in\mathbb{Z}$, also die ungeraden Vielfachen von $90^\circ$.
- Nun bleibt noch der zweite Faktor. Wegen $\sin^2(x)+\cos^2(x)=1$, dies ist der trigonometrische Pythagoras, gilt $\cos^2(x)=1-\sin^2(x)$ und damit
$\quad~~~1-\sin^2(x)-2 \sin^2(x)=1-3\sin^2(x)=0$.
- Diese Gleichung kannst du wie folgt umformen.
$\quad~~~\begin{array}{rclll} 1-3\sin^2(x)&=&0&|&+3\sin^2(x)\\ 1&=&3\sin^2(x)&|&:3\\ \frac13&=&\sin^2(x)&|&\sqrt{~~~}\\ \pm\frac1{\sqrt3}&=&\sin(x)&|&\sin^{-1}(~~~)\\ \pm35,3^\circ&\approx&x \end{array}$
- Zu jeder der beiden Lösungen kannst du ebenso wie oben zuerst die fehlende Basislösung bestimmen und damit dann die Lösungsgesamtheit.
Trigonometrische Gleichungen mit zwei Winkelfunktionen und unterschiedlichen Argumenten
Eine solche Gleichung ist zum Beispiel gegeben durch
$\cos(x)-\sin\left(\frac x2\right)=0$.
Hier tauchen nicht nur zwei verschiedene Winkelfunktionen auf, sondern auch noch verschiedene Argumente.
- Zunächst wird
$\quad~~~\cos(x)=\cos\left(2\cdot\frac x2\right)$
$\quad~~~$mit Hilfe eines Additionssatzes umgeschrieben:
$\quad~~~\cos\left(2\cdot \frac x2\right)=1-2\sin^2\left(\frac x2\right)$.
- Damit kann die obige Gleichung wie folgt geschrieben werden:
$\quad~~~1-2\sin^2\left(\frac x2\right)-\sin\left(\frac x2\right)=0$
- Dies ist eine quadratische Funktion in $\sin(x)$. Wenn du
$\quad~~~z=\sin\left(\frac x2\right)$ $\quad~~~$substituierst, erhältst du die quadratische Gleichung $1-2z\^2-z=0$. * Diese kannst du mit der **p-q-Formel** lösen. Hierfür stellst du die Gleichung um $-2z\^2-z+1=0$ und dividierst durch $-2$.
$\quad~~~\begin{array}{rclll} -2z\^2-z+1&=&0&|&:(-2)\\\ z\^2+\frac12z-\frac12&=&0\\\ z_{1,2}&=&-\frac14\pm\sqrt{\frac1{16}+\frac12}\\\ z_1&=&-\frac14+\frac34=\frac12\\\ z_2&=&-\frac14-\frac34=-1 \end{array}$
- Zuletzt resubstituierst du. Du musst also die folgenden Gleichungen lösen:
$\quad~~~~\sin\left(\frac x2\right)=\frac12$ sowie
$\quad~~~~\sin\left(\frac x2\right)=-1$.
- Dabei gehst du so vor wie in den obigen Beispielen zu $\sin(x)=c$.
Alle Videos zum Thema
Videos zum Thema
Gleichungen mit Sinus, Cosinus und Tangens (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gleichungen mit Sinus, Cosinus und Tangens (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 Trigonometrische Gleichungen
Trigonometrische Gleichungen
 Gleichungen mit Sinus, Cosinus und Tangens mit zwei Winkelfunktionen desselben Arguments
Gleichungen mit Sinus, Cosinus und Tangens mit zwei Winkelfunktionen desselben Arguments
 Gleichungen mit Sinus, Cosinus und Tangens mit zwei Winkelfunktionen verschiedener Argumente
Gleichungen mit Sinus, Cosinus und Tangens mit zwei Winkelfunktionen verschiedener Argumente









