Von der Koordinatenform in die Parameterform


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Von der Koordinatenform in die Parameterform
Nach dem Schauen dieses Videos wirst du in der Lage sein, eine Ebenengleichung in Koordinatenform in Parameterform umzuwandeln.
Zunächst lernst du, welche Bedingungen du bedenken solltest, wenn du eine Ebenengleichung in Parameterform aufstellen möchtest. Anschließend siehst du an einem Beispiel, wie du bei der Umwandlung von Koordinatenform in Parameterform vorgehen kannst. Abschließend erfährst du, wie du deine Rechnung überprüfen kannst.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Ebenengleichung, Parameterform, Normalenform, Koordinatenform, Stützvektor, Richtungsvektor, Normalenvektor, Skalarprodukt und Vektorprodukt.
Bevor du dieses Video schaust, solltest du bereits das Skalarprodukt und das Vektorprodukt kennen. Außerdem solltest du grundlegendes Wissen zu Ebenengleichungen in Parameter-, Normalen- und Koordinatenform haben.
Von der Koordinatenform in die Parameterform Übung
-
Beschreibe die Umwandlung einer Ebene von der Koordinatenform in die Parameterform.
TippsEbenengleichung in Parameterform:
$E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$
Dabei ist $\vec{p}$ der Stützvektor und die beiden Vektoren $\vec{u}$ und $\vec{v}$ sind die Richtungsvektoren.
Der Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
LösungEine Ebene können wir angeben in:
- Parameterform
- Normalenform
- Koordinatenform
Ebenengleichung in Parameterform:
$E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$
Dabei stellt $\vec{p}$ den Stützvektor, $\vec{u}$ und $\vec{v}$ stellen die Richtungsvektoren dar.
Ebenengleichung in Normalenform:
$E$: $(\vec{x} -\vec{p}) \cdot \vec{n} = 0$
Dabei stellt $\vec{p}$ den Stützvektor und $\vec{n}$ den Normalenvektor dar.
Ebenengleichung in Koordinatenform:
$E$: $ax+by+cz=d \qquad(a, b, c, d \in \mathbb{R})$
Wir können sehen, dass die Koordinatenform eine etwas andere Darstellung der Ebene ist und ohne Vektoren auskommt.
Wir betrachten die Umwandlung einer Ebene von der Koordinatenform in die Parameterform. Um die Ebene in Parameterform anzugeben, brauchen wir:
- einen Stützvektor: Der Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
- zwei Richtungsvektoren: Die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ spannen die Ebene auf. Sie können mit den Parametern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.
Bestimmung eines Stützvektors
Um den Stützvektor zu konstruieren, benötigen wir einen beliebigen Punkt auf der Ebene. Wir können beispielsweise für die $x$- und $y$-Koordinate einfach $0$ wählen, wodurch sich die $z$-Koordinate ergibt. Wir erhalten also den Stützvektor:
$\vec{p} = \begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}$
Zwischenschritt: Bestimmung des Normalenvektors
Um die Richtungsvektoren zu ermitteln, stellen wir zunächst den Normalenvektor der Ebene auf. Diesen können wir einfach aus den Koeffizienten in der Koordinatenform ablesen.
Bestimmung zweier Richtungsvektoren
Die Richtungsvektoren müssen linear unabhängig sein und orthogonal zum Normalenvektor verlaufen. Um sicherzugehen, dass die Richtungsvektoren orthogonal zum Normalenvektor verlaufen, legen wir fest, dass ihr Skalarprodukt mit dem Normalenvektor jeweils gleich null sein soll.
Wir betrachten zunächst den Richtungsvektor $\vec{u}$ und notieren das Skalarprodukt:
$\vec{u} \cdot \vec{n} =\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} \cdot \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}$
Wir müssen nun die Koordinaten des Richtungsvektors geschickt so wählen, dass das Skalarprodukt null ergibt:
$\vec{u} \cdot \vec{n} =\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} \cdot \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} = u_1 \cdot n_1 + u_2 \cdot n_2 + u_3 \cdot n_3$
Der zweite Richtungsvektor $\vec{v}$ muss auch orthogonal zum Normalenvektor sein. Beim zweiten Richtungsvektor müssen wir aber außerdem darauf achten, dass er linear unabhängig zum ersten Richtungsvektor ist. Das bedeutet: Es darf keine reelle Zahl $t$ geben, mit der man $\vec{u}$ multiplizieren kann, um $\vec{v}$ zu erhalten. Dies können wir einfach dadurch erreichen, indem wir ihn so konstruieren, dass er einen Nulleintrag in einer anderen Zeile hat als Vektor $\vec{u}$. Wir erhalten dann genauso durch geschicktes Wählen der anderen beiden Koordinaten den zweiten Richtungsvektor $\vec{v}$.
Abschließend können wir die Parameterform der Ebene notieren:
$E$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
-
Vervollständige die Bestimmung der Richtungsvektoren aus der Koordinatenform.
TippsDen Normalenvektor kannst du einfach aus den Koeffizienten in der Koordinatenform ablesen.
In der Rechnung ist in der zweiten Zeile jeweils das Skalarprodukt aus den Richtungsvektoren und dem Normalenvektor notiert. Dieses muss jeweils null ergeben, da Richtungsvektoren und Normalenvektor orthogonal zueinander sind.
Für das Skalarprodukt gilt:
$\vec{u} \cdot \vec{n} =\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} \cdot \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} = u_1 \cdot n_1 + u_2 \cdot n_2 + u_3 \cdot n_3 =0$
LösungWir betrachten die Umwandlung einer Ebene von der Koordinatenform in die Parameterform an einem Beispiel:
$E$: $2x+4y-2z=-8$
Um die Ebene in Parameterform anzugeben, brauchen wir:
- einen Stützvektor: Der Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
- zwei Richtungsvektoren: Die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ spannen die Ebene auf. Sie können mit den Parametern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.
Bestimmung eines Stützvektors
Um den Stützvektor zu konstruieren, benötigen wir einen beliebigen Punkt auf der Ebene. Wir können beispielsweise für die $x$- und $y$-Koordinate einfach $0$ wählen, wodurch sich die $z$-Koordinate ergibt:
$E$: $2 \cdot 0+4 \cdot 0-2z=-8 \quad \leftrightarrow \quad -2z=-8 \quad \leftrightarrow \quad z = 4$
Wir erhalten also den Stützvektor $\vec{p} = \begin{pmatrix} 0 \\ 0 \\ 4\end{pmatrix}$.
Zwischenschritt: Bestimmung des Normalenvektors
Um die Richtungsvektoren zu ermitteln, stellen wir den Normalenvektor der Ebene auf. Diesen können wir einfach aus den Koeffizienten in der Koordinatenform ablesen:
$\vec{n} = \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix}$
Diese Werte müssen wir also in die Lücken des Normalenvektors eintragen.
Bestimmung zweier Richtungsvektoren
Die Richtungsvektoren müssen linear unabhängig sein und orthogonal zum Normalenvektor verlaufen. Um sicherzustellen, dass die Richtungsvektoren orthogonal zum Normalenvektor verlaufen, legen wir fest, dass ihr Skalarprodukt mit dem Normalenvektor jeweils gleich null sein soll.
Wir betrachten den Richtungsvektor $\vec{u}$ und notieren zunächst allgemein das Skalarprodukt mit dem Normalenvektor:
$\vec{u} \cdot \vec{n} =\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix}$
Wir müssen nun die Koordinaten des Richtungsvektors geschickt so wählen, dass das Skalarprodukt null ergibt. In unserem Fall haben wir die erste und letzte Koordinate gegeben. Da $2 \cdot 2 = 4$ und $0 \cdot (-2)=0$ ist, können wir die so erhaltene $4$ hervorragend ausgleichen, indem wir $-1$ als zweite Koordinate einsetzen:
$\vec{u} \cdot \vec{n} =\begin{pmatrix} 2 \\ -1 \\ 0\end{pmatrix} \cdot \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix} = 2 \cdot 2 + (-1) \cdot 4 + 0 \cdot (-2) = 0$
Unser erster Richtungsvektor lautet also $\vec{u} = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix}$.
Der zweite Richtungsvektor $\vec{v}$ muss auch orthogonal zum Normalenvektor sein. Beim zweiten Richtungsvektor müssen wir aber außerdem darauf achten, dass er linear unabhängig zum ersten Richtungsvektor ist. Das bedeutet, es darf keine reelle Zahl $t$ geben, mit der man $\vec{u}$ multiplizieren kann, um $\vec{v}$ zu erhalten. Dies können wir einfach dadurch erreichen, indem wir ihn so konstruieren, dass er einen Nulleintrag in einer anderen Zeile hat als Vektor $\vec{u}$. In unserem Fall haben wir bereits die ersten beiden Koordinaten gegeben und ergänzen:
$\vec{v} \cdot \vec{n} =\begin{pmatrix} 0 \\ 1 \\ 2\end{pmatrix} \cdot \begin{pmatrix} 2 \\ 4 \\ -2 \end{pmatrix} = 0 \cdot 2 + 1 \cdot 4 + 2 \cdot (-2) = 0$
Unser zweiter Richtungsvektor lautet also $\vec{v} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix}$.
Wir können jetzt die Parameterform der Ebene notieren:
$E$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
-
Entscheide, welche Parameterform zu welcher Koordinatenform gehört.
TippsDu kannst die Aufgabe mithilfe der Punktprobe lösen.
Achte auf die Vorzeichen.
LösungUm zu überprüfen, welche Parameterform zu welcher Koordinatenform gehört, können wir die Punktprobe verwenden. Diese kann zwar allgemein keine eindeutige Zuordnung bieten, aufgrund der begrenzten Anzahl an zuzuordnenden Paaren bietet sie in dieser Aufgabe jedoch die schnellste Lösung.
Wir gehen wie folgt vor:
- Wir wählen zwei beliebige Zahlen für die Parameter $r$ und $s$.
- Danach setzen wir diese Zahlen in die Parameterform ein und berechnen daraus den Punkt.
- Nun setzen diesen Punkt in die Koordinatenform ein.
- Wir überprüfen, ob die sich so ergebende Gleichung korrekt ist.
1. $E$: $\vec{x} = \begin{pmatrix} 0 \\ -4 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -6 \\ 0 \\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Wir wählen $r=1$ und $s=2$ und erhalten:
$\vec{x} = \begin{pmatrix} 0 \\ -4 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} -6 \\ 0 \\ 3 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} = \begin{pmatrix} -6 \\ -12 \\ 9 \end{pmatrix}$
Jetzt setzen wir nacheinander in die gegebenen Koordinatenformen ein:
Einsetzen in $E_1$ ergibt:
$3 \cdot (-6) - 1 \cdot (-12) + 4 \cdot 9 = -18 + 12 +36 = 30 \neq 0 \rightarrow$ passt nicht!
Einsetzen in $E_2$ ergibt:
$1 \cdot (-6) + 4 \cdot (-12) - 2 \cdot 9 = -6 -48 -18 = -72 \neq 10 \rightarrow$ passt nicht!
Einsetzen in $E_3$ ergibt:
$2 \cdot (-6) + 3 \cdot (-12) + 4 \cdot 9 = -12 -36 + 36 = -12 \rightarrow$ passt!
$\Rightarrow$ zugehörige Ebene: $E_3$: $2x + 3y +4z = -12$
2. $E$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ -5 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ -1 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Wir wählen $r=2$ und $s=-1$ und erhalten:
$\vec{x} = \begin{pmatrix} 0 \\ 0 \\ -5 \end{pmatrix} + 2 \cdot \begin{pmatrix} 4 \\ -1 \\ 0 \end{pmatrix} - 1 \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 8 \\ -3 \\ -7 \end{pmatrix}$
Nun setzen wir nacheinander in die verbliebenen Koordinatenformen ein:
Einsetzen in $E_1$ ergibt:
$3 \cdot 8 - 1 \cdot (-3) + 4 \cdot (-7) = 24 + 3 -28 = -1 \neq 0 \rightarrow$ passt nicht!
Einsetzen in $E_2$ ergibt:
$1 \cdot 8 + 4 \cdot (-3) - 2 \cdot (-7) = 8 - 12 + 14 = 10 \rightarrow$ passt!
$\Rightarrow$ zugehörige Ebene: $E_2$: $x +4y -2z = 10$
3. $E$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ -4 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Wir wählen $r=1$ und $s=1$ und erhalten:
$\vec{x} = \begin{pmatrix} 0 \\ 0 \\ -4 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix}$
Jetzt setzen wir nacheinander in die verbliebenen Koordinatenformen ein:
Einsetzen in $E_1$ ergibt:
$3 \cdot 4 - 1 \cdot (-2) + 4 \cdot (-1) = 12 +2 -4 = 10 \neq 0 \rightarrow$ passt nicht!
Einsetzen in $E_4$ ergibt:
$ 3 \cdot (-2) +2 \cdot (-1) = -6 -2 = -8 \rightarrow$ passt!
$\Rightarrow$ zugehörige Ebene: $E_4$: $3y + 2z = -8$
4. $E$: $\vec{x} = r \cdot \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 4 \\ 1 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Diese Ebene können wir nun automatisch der Ebene $E_1$ zuordnen!
$\Rightarrow$ zugehörige Ebene: $E_1$: $3x - y +4z =0$
-
Berechne die fehlenden Werte in der Parameterform.
TippsSetze den Stützvektor in die Koordinatenform ein und löse nach $d$ auf.
Um die beiden Richtungsvektoren zu vervollständigen, musst du erst den Normalenvektor aus den Koeffizienten in der Koordinatenform ablesen.
Beispiel Ebene 1:
Normalenvektor: $\vec{n} = \begin{pmatrix} 3 \\ 6 \\ -1 \end{pmatrix} $
Erster Richtungsvektor: $\begin{pmatrix} 2 \\ e \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 6 \\ -1 \end{pmatrix} = 2 \cdot 3 + e \cdot 6 + 0 \cdot (-1) = 6 + 6e = 0$
$ \qquad \Rightarrow e=-1$
LösungUm eine Ebene von der Koordinatenform in die Parameterform umzuwandeln, ermitteln wir einen Stützvektor aus der Koordinatenform, indem wir beispielsweise für die $x$- und $y$-Koordinate $0$ wählen, wodurch sich die $z$-Koordinate ergibt. Anschließend lesen wir als Zwischenschritt den Normalenvektor aus den Koeffizienten in der Koordinatenform ab. Da die Richtungsvektoren orthogonal auf dem Normalenvektor stehen, müssen wir sie so wählen, dass jeweils das Skalarprodukt aus Richtungsvektor und Normalenvektor null ergibt. Abschließend können wir die Parameterform der Ebene notieren:
$E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$
Dabei ist der Vektor $\vec{p}$ der Stützvektor und die Vektoren $\vec{u}$ und $\vec{v}$ sind die Richtungsvektoren.
Wir führen dies für die gegebenen Ebenen durch:
Ebene 1: $E_1$: $3x + 6y -z =1$
In diese Ebene wird der Stützvektor mit $\begin{pmatrix} 0 \\ 0 \\ d\end{pmatrix}$ eingesetzt:
$0+0-d=1 \quad \Leftrightarrow \quad d=-1$
Aus der Koordinatenform können wir außerdem direkt den Normalenvektor ablesen:
$\vec{n} = \begin{pmatrix} 3 \\ 6 \\ -1 \end{pmatrix}$
Nun bestimmen wir die Richtungsvektoren:
- erster Richtungsvektor: $\begin{pmatrix} 2 \\ e \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 6 \\ -1 \end{pmatrix} = 2 \cdot 3 + e \cdot 6 + 0 \cdot (-1) = 6 + 6e = 0 \quad \Leftrightarrow \quad e=-1$
- zweiter Richtungsvektor: $\begin{pmatrix} 0 \\ 1 \\ f \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 6 \\ -1 \end{pmatrix} = 0 \cdot 3 + 1 \cdot 6 + f \cdot (-1) = 6 - f = 0 \quad \Leftrightarrow \quad f=6$
Damit ergibt sich folgende Parameterform der Ebene:
$E_1$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 1 \\ 6 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Ebene 2: $E_2$: $x - 4y + 3z =4$
In diese Ebene wird der Stützvektor mit $\begin{pmatrix} d \\ 0 \\ 0\end{pmatrix}$ eingesetzt:
$d+0+0=4 \quad \Leftrightarrow \quad d=4$
Aus der Koordinatenform können wir zudem direkt den Normalenvektor ablesen:
$\vec{n} = \begin{pmatrix} 1 \\ -4 \\ 3 \end{pmatrix}$
Jetzt bestimmen wir die Richtungsvektoren:
- erster Richtungsvektor: $\begin{pmatrix} e \\ 0 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -4 \\ 3 \end{pmatrix} = e \cdot 1 + 0 \cdot (-4) + 1 \cdot 3 = e + 3 = 0 \quad \Leftrightarrow \quad e=-3$
- zweiter Richtungsvektor: $\begin{pmatrix} f \\ -1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -4 \\ 3 \end{pmatrix} = f \cdot 1 + (-1) \cdot (-4) + 0 \cdot 3 = f + 4 = 0 \quad \Leftrightarrow \quad f=-4$
$E_2$: $\vec{x} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} -4 \\ -1 \\ 0 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
Ebene 3: $E_3$: $-2x -y + 6z =-2$
In diese Ebene wird der Stützvektor mit $\begin{pmatrix} 0 \\ d \\ 0\end{pmatrix}$ eingesetzt:
$0-d+0=-2 \quad \Leftrightarrow \quad d=2$
Aus der Koordinatenform können wir außerdem direkt den Normalenvektor ablesen:
$\vec{n} = \begin{pmatrix} -2 \\ -1 \\ 6 \end{pmatrix}$
Nun bestimmen wir die Richtungsvektoren:
- erster Richtungsvektor: $\begin{pmatrix} 1 \\ e \\ 0 \end{pmatrix} \cdot \begin{pmatrix} -2 \\ -1 \\ 6 \end{pmatrix} = 1 \cdot (-2) + e \cdot (-1) + 0 \cdot 6 = -2 -e = 0 \quad \Leftrightarrow \quad e=-2$
- zweiter Richtungsvektor: $\begin{pmatrix} 0 \\ 6 \\ f \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -4 \\ 3 \end{pmatrix} = 0 \cdot (-2) + 6 \cdot (-1) + f \cdot 6 = -6 + 6f = 0 \quad \Leftrightarrow \quad f=1$
Damit ergibt sich folgende Parameterform der Ebene:
$E_3$: $\vec{x} = \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 6 \\ 1 \end{pmatrix} \qquad(r, s \in \mathbb{R})$
-
Benenne die in der Parameterform enthaltenen Vektoren.
TippsDer Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
Die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ spannen die Ebene auf. Sie können mit den Parametern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.
Der Normalenvektor taucht in der Ebenengleichung in Parameterform nicht auf.
LösungDie Parameterform
Die allgemeine Ebenengleichung in Parameterform lautet:
$E$: $\vec{x}=\vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \qquad(r, s \in \mathbb{R})$
Der Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
Die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ spannen die Ebene auf. Sie können mit den Parametern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.In unserer Formel gilt also:
$E$: $\vec{x} =\underbrace{\begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix}}_{\text{Stützvektor}} + r \cdot \underbrace{\begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix}}_{\text{Richtungsvektor}} + s \cdot \underbrace{\begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix}}_{\text{Richtungsvektor}} \qquad(r, s \in \mathbb{R})$
Hinweis: Der Normalenvektor taucht in der Ebenengleichung in Parameterform nicht auf. Er ist nur in der Normalenform der Ebene enthalten.
-
Überprüfe die Aussagen.
TippsNur eine der Aussagen ist korrekt.
Der Vektor $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ wird auch Nullvektor genannt. Seine Länge ist null. Er hat keine bestimmte Richtung.
Der Stützvektor $\vec{p}$ verläuft immer vom Ursprung zu einem beliebigen Punkt auf der Ebene (dem Stützpunkt).
Die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ spannen die Ebene auf. Sie können mit den Parametern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.LösungWir überprüfen die gegebenen Aussagen:
Aussage 1:
- Der Vektor $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $ ist als Stützvektor nicht möglich.
Aussage 2:
- Der Vektor $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $ ist als Richtungsvektor nicht möglich.
Aussage 3:
- Richtungsvektor und Stützvektor können nicht identisch sein.
Aussage 4:
- Ein Richtungsvektor darf maximal eine Nullkoordinate haben.
9.892
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.307
Lernvideos
38.669
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?



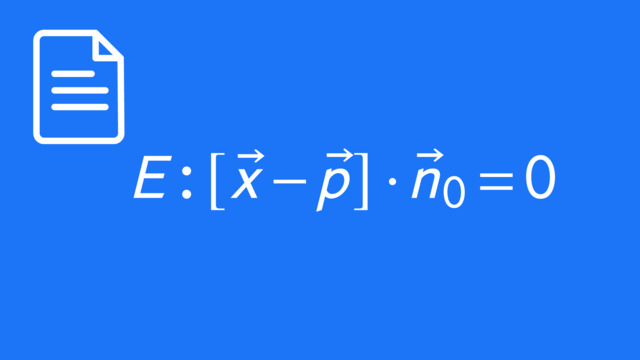










Danke!!!!