Verwendung von Zirkel und Geodreieck
Mit Hilfe von Geodreieck und Zirkel kannst du sehr vieles konstruieren. Hier lernst du die Konstruktion von Lot und Parallele kennen.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was sind Parallele und Lot?
Parallele und senkrechte Geraden sind jeweils Geraden, die sich in einer bestimmten Position zu einer anderen Geraden befinden.
Eine Parallele hat zu der anderen Geraden an jeder Stelle den gleichen Abstand. Zwei Geraden, die zueinander parallel sind, schneiden sich in keinem Punkt.
Hier siehst du zwei zueinander parallele Geraden $g$ und $h$.

Den Begriff des „Lotes“ findest du im Handwerk: Ein Lot ist ein an einem Faden aufgehängtes Metallstück zur Bestimmung einer Senkrechten.
Daraus erkennst du: Bei einem Lot handelt es sich um eine senkrechte Gerade. Ein Lot schneidet die Gerade also in einem Punkt. Würde man den Winkel zwischen den beiden Geraden messen, wäre er immer $90^\circ$.
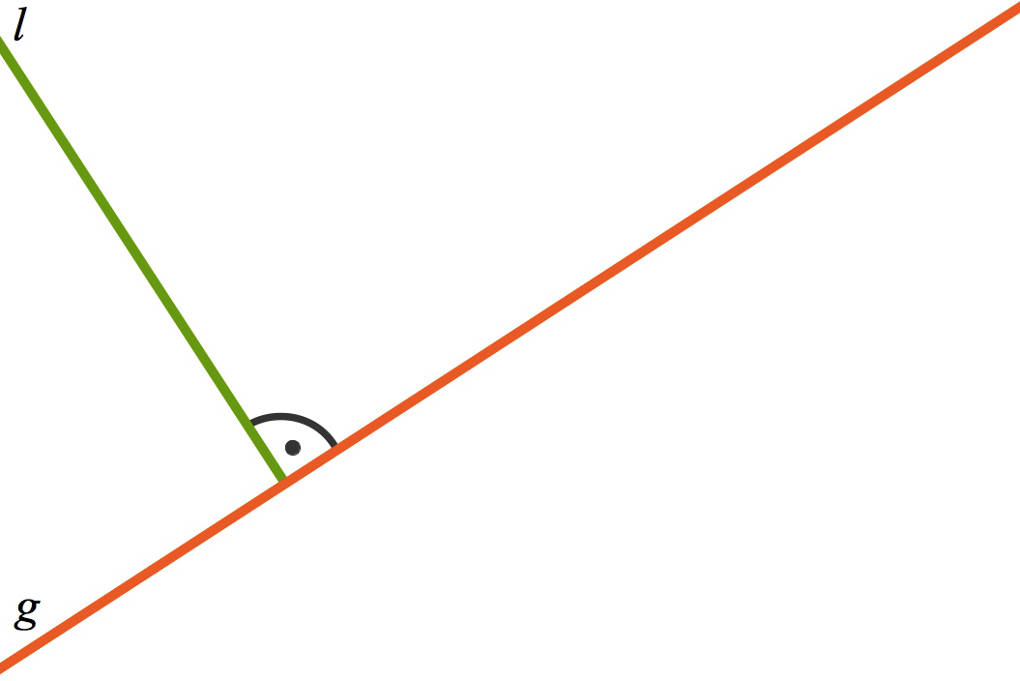
Konstruktion eines Lotes
Bei der Konstruktion eines Lotes kannst du entweder Lineal und Zirkel oder das Geodreieck verwenden.
Bei der Konstruktion mit dem Geodreieck legst du das Geodreieck mit der Mittellinie auf die Ausgangsgerade. Die lange Seite des Geodreiecks liegt nun senkrecht zu der Geraden. Jetzt kannst du Geodreieck so lange verschieben, bis es sich an dem Punkt befindet, an dem das Lot gezeichnet werden kann. Zeichne dort die zweite Gerade ein.
Beachte aber: Die Konstruktion mit dem Geodreieck ist zwar schneller und du findest sie vielleicht einfacher, allerdings ist sie auch ungenauer.
Bei der Konstruktion mit Zirkel und Lineal unterscheidet sich die Vorgehensweise etwas, je nachdem ob der Punkt, an dem das Lot anliegen soll, auf der Ausgangsgeraden liegt oder darüber.
Wir schauen uns nun die Konstruktion des Lots von einem Punkt $P$ auf die Gerade $g$ an. $P$ liegt nicht auf $g$.
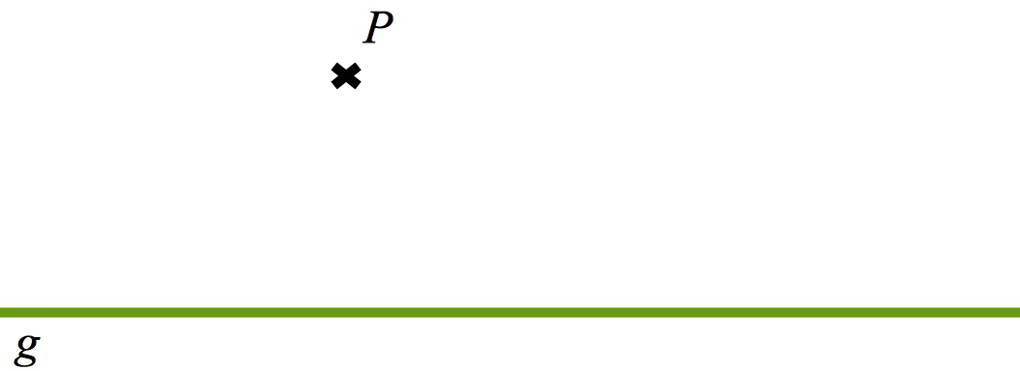
- Zeichne einen Kreisbogen um $P$, welcher die Gerade $g$ in zwei Punkten schneidet.
- Um jeden der beiden Punkte zeichnest du je einen Kreisbogen mit dem gleichen Radius. Diese Kreisbögen schneiden sich in zwei Punkten.
- Wenn du diese Punkte verbindest, erhältst du das Lot von dem Punkt $P$ auf die Gerade $g$.
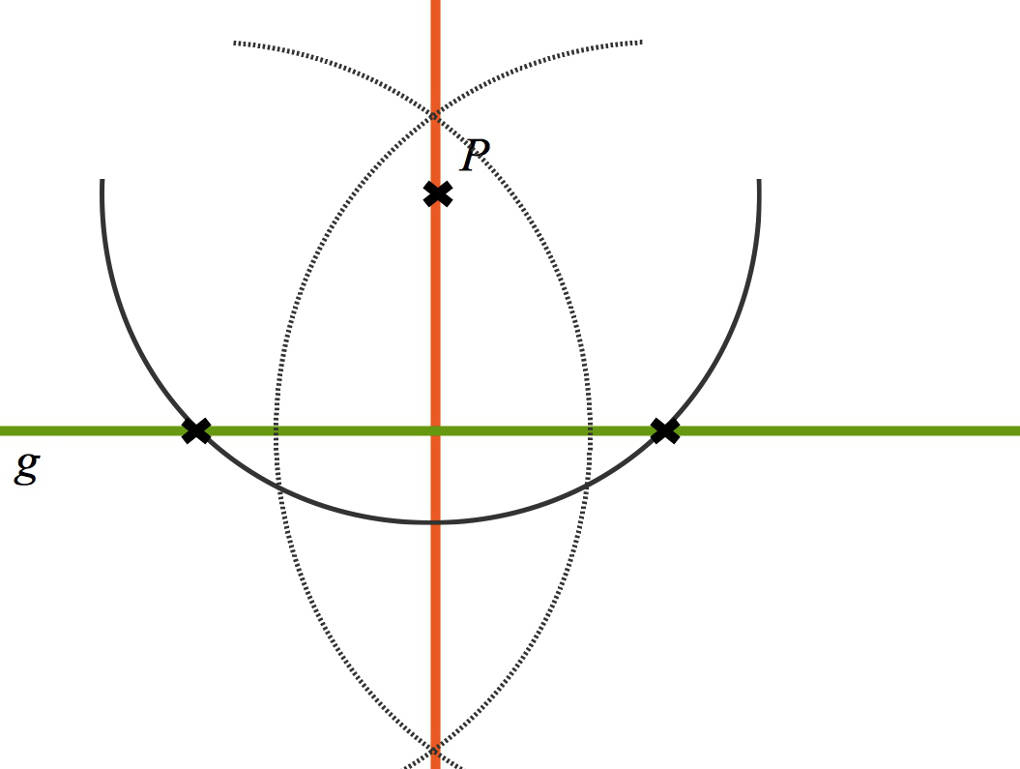
Liegt der Punkt $P$ auf der Geraden, gehst du bei der Konstruktion ganz ähnlich vor. Als Mittelpunkt für den Kreisbogen wählst du auch hier den Punkt $P$. Zeichnest du nun den Kreisbogen, erhältst du wieder zwei Schnittpunkte. Die folgenden Schritte sind die gleichen wie bei der Konstruktion mit einem Punkt über der Geraden.
Konstruktion einer Parallelen
Auch bei der Konstruktion einer Parallelen kannst du entweder Zirkel und Lineal oder das Geodreieck nutzen.
Bei der Konstruktion mit dem Geodreieck nutzt du diesmal die parallelen Hilfslinien. Sie befinden sich auf dem Geodreieck zwischen den Winkelskalen. Zur Konstruktion legst du ein Geodreieck mit der langen Seite an die Ausgangsgerade. Anschließend verschiebst du dein Geodreieck nach oben, bis eine der Hilfslinien sich mit der Ausgangsgeraden deckt. Nun kannst du die Parallele einzeichnen.
Auch hier gilt wieder, die Konstruktion mit dem Geodreieck ist etwas ungenau. Brauchst du also eine exakte Parallele, probiere doch einmal die Konstruktion mit Zirkel und Lineal.
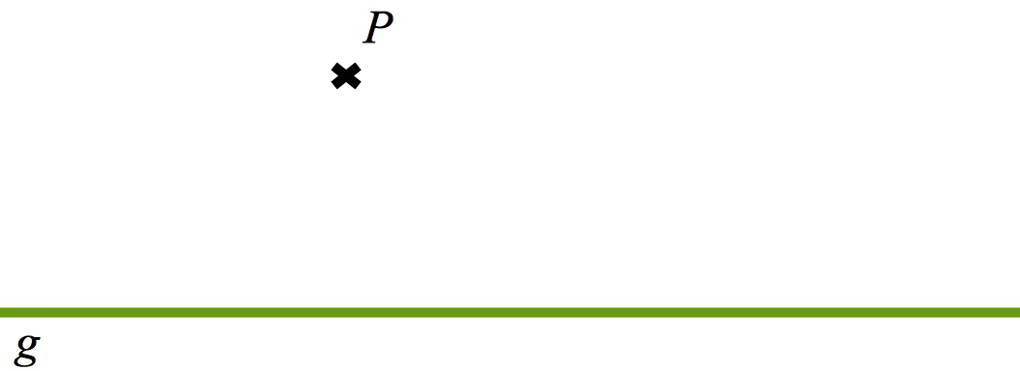
Zur Konstruktion einer Parallelen zu der Geraden $g$ durch den Punkt $P$ gehst du wie folgt vor:
Zunächst konstruierst du eine Senkrechte auf $g$ durch den Punkt $P$. Dies machst du so, wie du es beim Lot bereits gesehen hast.

Nun konstruierst du auf die gleiche Art eine Senkrechte $h$ auf diese Senkrechte. Somit ist die Gerade $h$ parallel zu der Geraden $g$.
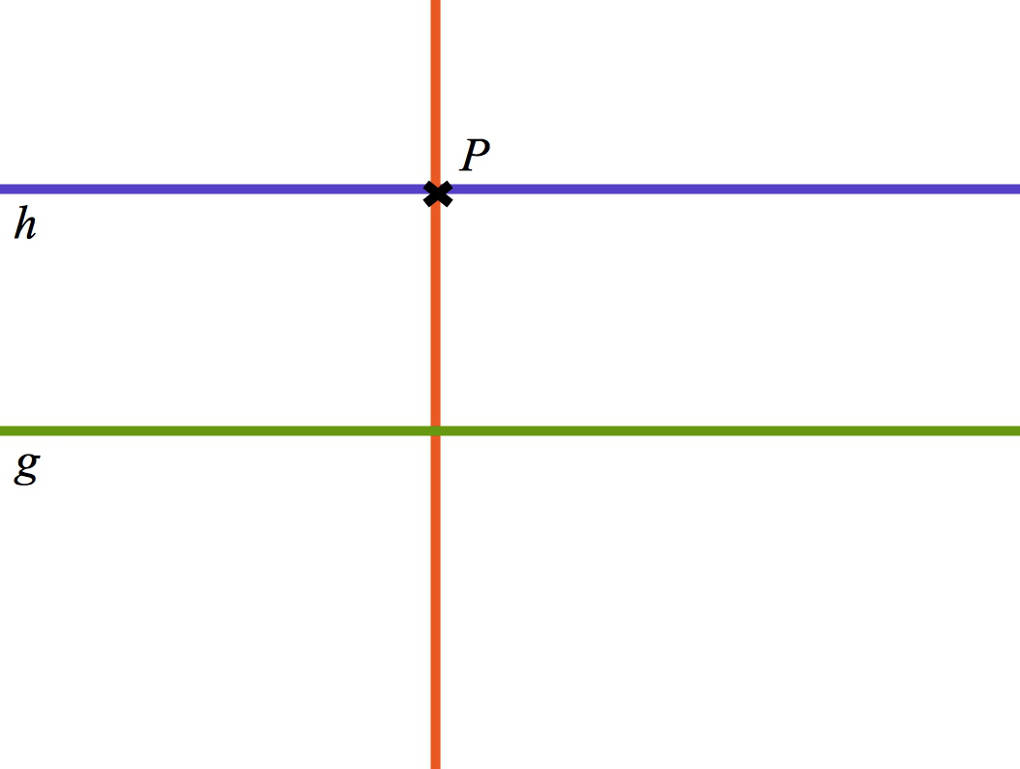
Schließlich kannst du auch eine Parallele in einem gegebenen Abstand zu der Geraden $g$ konstruieren:
- Fälle das Lot auf die Gerade $g$ in einem beliebigen Punkt der Geraden.
- Nun kannst du auf diesem Lot einen Punkt ermitteln, welcher den gegebenen Abstand zu der Geraden hat.
- Zuletzt konstruierst du in diesem Punkt wieder eine Senkrechte. Dies ist die gesuchte Parallele zu $g$.
Alle Videos zum Thema
Videos zum Thema
Verwendung von Zirkel und Geodreieck (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Verwendung von Zirkel und Geodreieck (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung






 Winkel und parallele Geraden mit dem Geodreieck zeichnen
Winkel und parallele Geraden mit dem Geodreieck zeichnen
 Grundkonstruktionen mit Zirkel und Lineal: Strecken und Winkel übertragen
Grundkonstruktionen mit Zirkel und Lineal: Strecken und Winkel übertragen
 Konstruktion einer Parallelen
Konstruktion einer Parallelen
 Konstruktion eines Lotes
Konstruktion eines Lotes









