Funktionsgleichungen
Die Funktionsgleichung einer Funktion sagt aus, dass jedem x genau ein Wert y zugeordnet werden kann. Hier erfährst du, worin sich explizite und implizite Funktionsgleichungen unterscheiden und wie so eine Gleichung dargestellt wird.
Inhaltsverzeichnis zum Thema
Was ist eine Funktion?
Eine Funktion ist eine spezielle Zuordnung. Bevor wir also verstehen, was eine Funktion ist, sollten wir kurz untersuchen, was überhaupt eine Zuordnung ist.
Was ist eine Zuordnung?
Bei einer Zuordnung stehen Größen zueinander in einer Beziehung:
- Du kannst jedem deiner Freunde die Namen seiner Geschwister zuordnen, sofern er welche hat.
- Anstatt jedem Freund die Namen seiner Geschwister zuzuordnen, könntest du ihm auch die Anzahl seiner Geschwister zuordnen.
Worin liegt der Unterschied zwischen diesen beiden Zuordnungen? Betrachten wir ein Beispiel:
- Paul hat zwei Geschwister: Luke und Phoebe.
- Niko hat eine Schwester: Lilly.
- Lucy hat zwei Geschwister: Anna und Jasper.
Bei der Zuordnung „Freund zu Namen der Geschwister“ wird Paul mehr als ein Element (Name) zugeordnet, nämlich Luke und Phoebe. Niko wird nur ein Name zugeordnet.
Bei der Zuordnung „Freund zu Anzahl der Geschwister“ gehört zu jedem der drei Freunde genau ein Element, nämlich zu Paul und Luca $2$ und zu Niko $1$.
Das ist ein wichtiger Unterschied. Denn eine Zuordnung, bei der einer Größe genau eine andere Größe zugeordnet wird, wird Funktion genannt.
Beispiel für eine Funktion
Paul liebt Pizza. Er geht mit seiner Familie oft in eine Pizzeria. Dort gibt es manchmal ein besonderes Angebot: Eine einfache Pizza mit Tomatensauce und Käse kostet $3,50~€$. Jeder Gast kann die Zutaten und auch die Anzahl der Zutaten selbst bestimmen. Jede weitere Zutat kostet $1,20~€$. Dadurch können verschiedene Preise zustande kommen, je nachdem, wie viele Zutaten gewählt werden:
- Paul überlegt sich, wie viel seine Pizza kostet, wenn er vier Zutaten auswählt: $1,20~€\cdot 4~+~3,50~€~=~8,30~€$.
- Seine Schwester Phoebe nimmt zwei Zutaten: $1,20~€\cdot 2~+~3,50~€~=~5,90~€$.
- Sein Bruder Luke nimmt fünf Zutaten: $1,20~€\cdot 5~+~3,50~€~=~9,50~€$.
- Seine Mutter nimmt ebenfalls zwei Zutaten. So ergibt sich wie bei seiner Schwester $5,90~€$.
- Sein Vater nimmt drei Zutaten: $1,20~€\cdot 3~+~3,50~€~=~7,10~€$.
Paul fällt auf, dass sich mit der Anzahl der Zutaten der Preis ändert:
$1,20~€ \cdot \underline{\qquad} + 3,50~€ = \underline{\qquad}$
Wenn Paul auf der linken Seite jeweils die Anzahl der Zutaten einsetzt und den Term berechnet, erhält er auf der rechten Seite das Ergebnis.
Diese Zuordnung ist eine Funktion.
Darstellungen von Funktionsgleichungen
In dem obigen Beispiel kann die Anzahl der Zutaten durch die Variable $x$ ersetzt werden:
$1,2\cdot x+3,5$.
Der Wert, also der zu bezahlende Betrag, der herauskommt, wird ebenfalls mit einer Variablen bezeichnet. Wir nehmen dafür $y$:
$y=1,2\cdot x+3,5$.
Dies ist eine Funktionsgleichung. Sie besagt, dass jedem $x$ genau ein Wert $y$ zugeordnet wird. Eine solche Funktionsgleichung wird als explizite Funktionsgleichung oder Funktionsgleichung in Normalform bezeichnet. Oft wird anstelle von „Funktionsgleichung“ auch kurz nur von „Funktion“ gesprochen.
Eine Funktion kannst du auch wie folgt schreiben:
- $f(x)=1,2\cdot x+3,5$ oder
- $f:~x~\rightarrow~1,2\cdot x+3,5$
Die Menge, in der sich die $x$ befinden, wird als Definitionsmenge oder Definitionsbereich bezeichnet und die Menge, in der sich die $y$ befinden, als Wertemenge oder Wertebereich.
Implizite Funktionsgleichungen
Eine Funktionsgleichung kann auch implizit gegeben sein: $2y+4x=8$.
Du siehst, dass in dieser Gleichung beide Variablen $x$ und $y$ auf der gleichen Seite stehen. Diese Gleichung hat nicht die Form wie die oben angegebenen Funktionsgleichungen. Du kannst sie jedoch durch Äquivalenzumformungen in die Normalform bringen:
$\begin{array}{rclll} 2y+4x&=&8&|&-4x\\ 2y&=&-4x+8&|&:2\\ y&=&-2x+4 \end{array}$
Dies ist eine Funktionsgleichung in Normalform.
Darstellung von Funktionen im Koordinatensystem
Um den Verlauf einer Funktion darzustellen, verwendest du ein Koordinatensystem. Ein Koordinatensystem hat ein horizontale Achse, die x-Achse, und eine vertikale Achse, die y-Achse.
Lass uns nochmal auf die Funktion $y=1,2x+3,5$ zurückkommen.
Wir wollen für diese Funktion nun eine Wertetabelle erstellen. Hierfür berechnest du zu einigen $x$ den zugehörigen $y$-Wert und erhältst somit Punkte $(x|y)$.
Zum Beispiel gehört zu $x=2$ der folgende $y$-Wert:
$y=1,2\cdot 2+3,5=2,4+3,5=5,9$.
Wenn du das für einige Werte gemacht hast, könnte dies so aussehen:
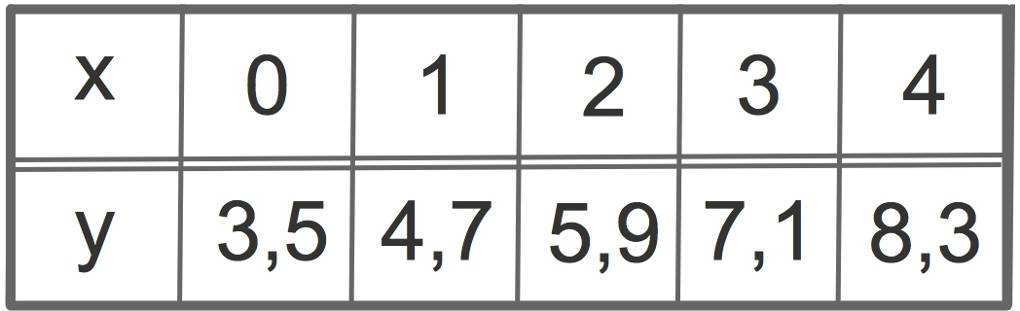
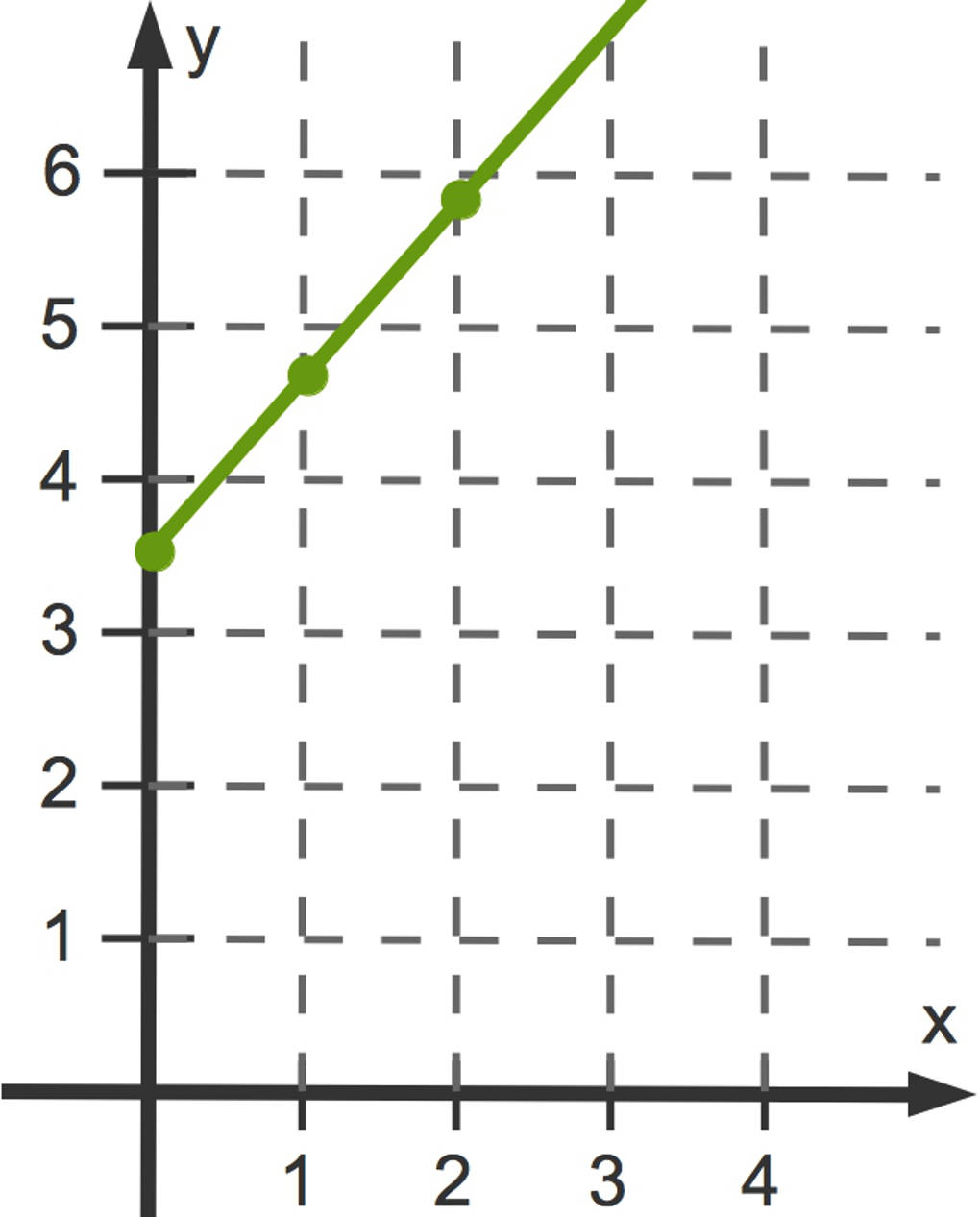
Jeden dieser Punkte kannst du in ein Koordinatensystem einzeichnen. Dies siehst du hier für die Punkte $(0|3,5)$, $(1|4,7)$ sowie $(2|5,9)$. Wenn du die Punkte miteinander verbindest, hast du den Funktionsgraphen gezeichnet. Hier ist es eine Gerade.
Alle Videos zum Thema
Videos zum Thema
Funktionsgleichungen (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Funktionsgleichungen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung



 Eigenschaften verschiedener Funktionstypen
Eigenschaften verschiedener Funktionstypen
 Lineare und nichtlineare Funktionen
Lineare und nichtlineare Funktionen
 Funktionsarten identifizieren
Funktionsarten identifizieren









