Teilchen als Welle
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Teilchen als Welle
Teilchen als Welle
In diesem Text soll nachvollzogen werden, wie Anfang des 20. Jahrhunderts die Idee aufkam, dass nicht nur das Licht sowohl Teilchen- als auch Wellencharakter habe, sondern dass dies überhaupt für alle Elementarteilchen gelten müsse. Diese Vorstellung wurde von dem französischen Physiker Louis de Broglie postuliert.
Die Teilcheneigenschaft des Lichts
In der klassischen Optik gab es bereits seit Längerem zwei Modelle, die dafür verwendet wurden, um die Phänomene des Lichts zu beschreiben: das Strahlen- und das Wellenmodell. Mit keinem der Modelle war man in der Lage, sämtliche Phänomene des Lichts zu beschreiben, aber beide zusammen ergänzten sich gut. So war es beispielsweise nicht möglich, die Interferenz und Polarisation von Licht mit dem Strahlenmodell zu erklären. Dabei war aber klar, dass das Strahlenmodell eine etwas grobe Vorversion des Wellenmodells war und das Wellenmodell das eigentlich gültige Modell des Lichts ist.
Andererseits gab es Experimente, die nicht mit dem Wellenmodell verstanden werden können, z. B. den Fotoeffekt, den Albert Einstein in seiner berühmten Veröffentlichung von 1905 diskutierte.
Einsteins Lichtquantenhypothese
Die Wechselwirkung zwischen Licht und Materie finden über Lichtquanten, die Photonen, statt. So wird Energie von den Elektronen in der Materie in diskreten „Energiepaketen“ von Photonen übertragen. Diese Tatsache deutet sehr stark auf einen Teilchencharakter. Diese Energie ist abhängig von der Frequenz $f$ des Lichts: $E = h \cdot f$. Der Proportionalitätsfaktor ist das plancksche Wirkungsquantum $h$.
Im Jahr 1922 hat der US-amerikanische Physiker Arthur Holly Compton Röntgenstrahlen auf Elektronen geschossen und ihr Streuverhalten untersucht. Auch er fand, dass diese Zusammenstöße sich mathematisch wie ein gewöhnlicher elastischer Stoß zwischen einem Photon und einem Elektron behandeln ließen. Dieser Effekt wird auch Compton-Effekt genannt. Mit dieser Erkenntnis verfestigte sich weiterhin die Vorstellung, dass Licht aus Teilchen bestehe.
In den 1920er-Jahren gab es also eine lebhafte Diskussion um die Frage nach der Natur des Lichts. Ist es nun Welle oder Teilchen?
Die Welleneigenschaft der Materie
Inmitten dieser Debatte hatte der französische Physiker Louis de Broglie die Idee, Einsteins Perspektive von den Füßen auf den Kopf zu stellen. Einstein hat für das Licht eine Eigenschaft, die auf Wellen bezogen wurde – die Frequenz –, auf Eigenschaften wie die Masse und den Impuls bezogen, die als für Teilchen typisch angesehen wurden. In der klassischen Vorstellung findet bei einer Welle ein Energietransport statt, aber kein Materietransport. Das bedeutet, dass kein Transport lokalisierter Materie gegebener Masse von einem Ort zu einem anderen stattfinden sollte.
De Broglie dreht die Perspektive Einsteins um und verallgemeinert sie zugleich vom Licht auf alle Materie: Zu jeder Masse gehört eine Frequenz und zu jedem Impuls gehört eine Wellenlänge – und umgekehrt. Damit wird vorstellbar, dass nicht nur Licht eine Masse haben könnte, sondern dass alles, was Masse hat, auch eine Frequenz hat und wellenartig ist.
Die Beziehung zwischen der Energie und der Frequenz von Licht, die von Einstein aufgestellt wurde, wird von De Broglie für beliebige Elementarteilchen wie Elektronen oder Protonen verallgemeinert. Dazu stützt er sich auf Einsteins Energie-Masse-Relation $E = m \cdot c^2$ aus der speziellen Relativitätstheorie.
$E = h \cdot f = m \cdot c^2 \quad \Leftrightarrow \quad m \cdot c = \dfrac{h \cdot f}{c}$
Gehen wir nun davon aus, dass die Ausbreitungsgeschwindigkeit $c$ einer Welle auch gleichzeitig die Geschwindigkeit eines Teilchens $v$ ist, dann können wir $m \cdot c = p$ durch den Impuls $p$ eines Teilchens ersetzen. Zusätzlich kennen wir die Beziehung $c = \lambda \cdot f$ zwischen der Wellenlänge $\lambda$, der Frequenz $f$ und der Ausbreitungsgeschwindigkeit $c$ einer Welle. Damit ergibt sich:
$p = \dfrac{h \cdot f}{c} \quad \Leftrightarrow \quad p = \dfrac{h \cdot f}{\lambda \cdot f} \quad \Leftrightarrow \quad p = \dfrac{h}{\lambda} \quad \Leftrightarrow \quad \lambda = \dfrac{h}{p}$
Materiewellen nach De Broglie
De Broglie postulierte 1924, dass sich Einsteins Erkenntnisse auf alle Elementarteilchen übertragen ließen und gültig seien. Demzufolge können einem Elementarteilchen, das die Energie $E$ und einen Impuls $p$ hat, eine Frequenz $f$ und eine Wellenlänge $\lambda$ zugeordnet werden.
$f = \dfrac{E}{h}~$ und $~\lambda = \dfrac{h}{p}$
Somit haben alle Elementarteilchen Welleneigenschaften.
Interessanterweise wurde unabhängig von de Broglie gerade ein Experiment durchgeführt, mit dem die Welleneigenschaften von Elektronen untersucht werden konnten. Clinton Davisson und Lester Germer schossen in den Jahren 1923–1927 Elektronen mit einer Energie von etwa $100~\text{eV}$ auf Nickeleinkristalle. Dies entspricht einer De-Broglie-Wellenlänge von ${\lambda = 1{,}2 ~\text{\AA} = 1{,}2\cdot 10^{-10}~\text{m}}$. Da diese Kristalle ein periodisches, sehr feinmaschiges Gitter bilden, bei dem die Atome einen Abstand etwa in der Größenordnung der von de Broglie postulierten Wellenlänge der Elektronen haben, sollte man Beugungs- und Interferenzeffekte sehen können. Tatsächlich fanden sie Interferenzerscheinungen und bestätigten damit den Wellencharakter von Elektronen. Auch Claus Jönsson hatte 1961 bei einem Doppelspaltexperiment mit Elektronen ihren Wellencharakter feststellen können.
Die Teilchenartigkeit von Wellen
Nachdem de Broglie alle Materie mit Welleneigenschaften versehen hatte, stellt sich die Frage, wie die typischen Eigenschaften von Teilchen in seinem Modell wiedergefunden werden können: Lokalisierung und Materietransport. De Broglie schlug vor, lokalisierte Materie im Rahmen der Wellentheorie als Energieklumpen mit Welleneigenschaft zu verstehen. Gemäß der klassischen Vorstellung findet bei einer Welle ein Energietransport statt, aber kein Materietransport.
Wenn der scharfe Unterschied zwischen Energie und Materie aufgehoben würde, indem Materie als Energieklumpen aufgefasst wird, sollte also auch etwas wie ein Materietransport im Rahmen einer Wellentheorie vorstellbar sein.
Seine Idee beruht auf den Eigenschaften von kohärenten und ebenen Wellen, die sich in Form von Wellenfronten ausbreiten. Dabei wird die Geschwindigkeit der Wellenfronten als Phasengeschwindigkeit bezeichnet.
Diese Wellen können miteinander interferieren und je nach Phasenverschiebung konstruktiv oder destruktiv interferieren, wodurch sich eine verstärkte oder ausgelöschte Resultante ergibt.
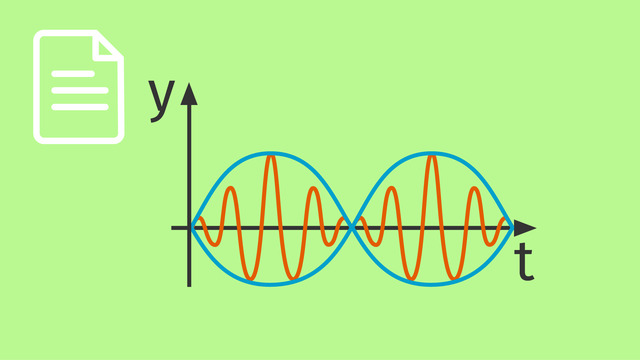
Werden nun Wellen mit unterschiedlicher Frequenz überlagert, kommt es zum Phänomen der Schwebung. Dadurch kommt es zur Amplitudenmodulation, wodurch sich eine einhüllende Welle um die laufende Welle bildet.
Auf diese Art und Weise können Wellenpakete entstehen, die eine lokalisierte Welle darstellen. Diese Wellenpakete breiten sich mit der Phasengeschwindigkeit der einhüllenden Welle aus – der sogenannten Gruppengeschwindigkeit $v_G$.
Zusammenfassung – Teilchen als Welle
- Am Anfang des 20. Jahrhunderts zeigte sich zum Beispiel durch den Fotoeffekt, dass Licht nicht nur als elektromagnetische Welle angesehen werden kann. Dem Licht wurde durch den Fotoeffekt auch Teilchencharakter zugeschrieben. Albert Einstein formulierte dies in seiner Lichtquantenhypothese, dass Licht in diskreten „Energiepaketen“, den Photonen, übertragen wird.
-
Einige Jahre später untersuchte Louis de Broglie die Welleneigenschaften von Teilchen wie Elektronen und schrieb ihnen eine Frequenz $f$ und eine Wellenlänge $\lambda$ zu:
$f = \dfrac{E}{h}$ und $\lambda = \dfrac{h}{p}$
Bei diesen Welleneigenschaften von Teilchen wie Elektronen konnten Interferenz- und Beugungsmuster nachgewiesen werden.
- Die Vorstellung der diskreten Lichtquanten kann mithilfe einer Überlagerung von Wellen unterschiedlicher Frequenzen erklärt werden. Durch Schwebung und Amplitudenmodulation bilden sich lokalisierte Wellenpakete, die sich mit einer Gruppengeschwindigkeit fortbewegen.
Häufig gestellte Fragen zum Thema Teilchen als Welle
Teilchen als Welle Übung
-
Nenne die Neuigkeiten aus der Welt der Wellen und Teilchen.
TippsBei der Compton-Streuung wurde mit Licht ein Elektron bewegt/angestoßen.
LösungDamals ging man davon aus, dass Licht eine Welle sei und sich auch nur wie eine solche verhält.
Man konnte aber zeigen, dass Wellen (nicht nur Licht) auch Teilcheneigenschaften haben. Dies nennt man „Welle-Teilchen-Dualismus"
Mit dem Beweis der Compton-Streuung galt dies ebenfalls als bewiesen, da bei der Compton-Streuung ein Teilchen, zum Beispiel ein Elektron, durch ein Photon angestoßen wurde. Dabei wurde ebenfalls wieder Licht frei.
Licht konnte also ein Teilchen bewegen, und musste dadurch selbst ein Teilchen sein.
Dass dies mit der geometrischen Optik vereinbar ist, erklärte De Broglie, indem er sagte: Die Strahlen, mit denen man in der geometrischen Optik arbeitete, verliefen senkrecht zur Ausbreitungsrichtung der Wellenfronten.
-
Beschreibe die dynamische Masse und die Trägheit.
TippsBei einer Gleichung ähnlich $m\cdot v= z$ , wobei $v$ maximal ist, kann $z$ nur größer werden, wenn $m$ stattdessen wächst.
LösungMit der dynamischen Masse wurde das Verständnis von Masse verändert.
Masse war nicht länger eine Konstante, sondern eine Größe die sich bei Geschwindigkeiten nahe der Lichtgeschwindigkeit veränderte.
Die Energiegleichung für die relativistische Energie
$W=mc^2$
zeigt, dass die Energie bei Lichtgeschwindigkeit nur noch von der Masse abhängig ist, bzw. andersherum steigende Energie eine steigende Masse zur Folge hat.
Die Masse wird also auch geschwindigkeitsabhängig.
Eine veränderte Masse sorgt dann auch für eine veränderte Trägheit, da Trägheit eben von der Masse abhängig ist.
-
Beschreibe De Broglies Erkenntnisse.
TippsÜberlege, ob bei den Gleichungen gekürzt werden könnte, und ob sie dann noch stimmen.
Welche neue Eigenschaft wurde Teilchen zugeordnet?
LösungDe Broglie hat viele Entdeckungen gemacht, die zum Teil erst mit dem Beweis der allgemeinen Relativitätstheorie bewiesen wurden.
Er fand heraus, dass die Energie eines Teilchens gleich der einer Welle ist
$mc^2=hf$,
und die Masse damit frequenzabhängig ist
$m=\dfrac{hf}{c^2}$.
Der entscheidende Beweis dafür wurde im Zuge der Relativitätstheorie geliefert, bei der nachgewiesen wurde, dass Licht durch Gravitation abgelenkt werden kann.
Die Wellenlänge die De-Broglie-Teilchen zuordnete, nennt man De-Broglie-Wellenlänge $\lambda=\dfrac{h}{p}$, wobei $p$ der Impuls eines Photons $mc$ ist.
-
Beschreibe, was Wellenpakete sind und was eine Phasenverschiebung bewirkt.
TippsÜberlege, wie die Y-Werte eines Wellendiagramms aussehen, wenn man 2 gleiche Wellen auf der X-Achse zueinander verschiebt. Daran kann man dann sehen, wie sie sich beeinflussen, wenn sie sich überlagern.
Überlege, was wechselnde Phasenverschiebung mit der Amplitude macht.
LösungÜberlagert man 2 oder mehr Wellen, so muss man aufpassen, mit welcher Phasenverschiebung dies geschieht.
Sollen sich 2 Wellen gleicher Frequenz und Amplitude verstärken (addieren), müssen sie gleichphasig sein, d.h., Wellenberg muss auf Wellenberg stehen.
Eine Auslöschung beider Wellen entsteht, wenn ihre Phasenverschiebung zueinander 180° beträgt, also Wellenberg auf Wellental steht.
Liegt die Phasenverschiebung dazwischen, ist die resultierende Amplitude ebenfalls zwischen der Summe beider Amplituden und 0.
Sind die Frequenzen unterschiedlich, wechselt die Phasenverschiebung ständig, da die Phasengeschwindigkeit der einen Welle größer ist als die der anderen (bei höheren Frequenzen sind die Wellenberge näher beieinander).
Ist dies der Fall, so entstehen Gruppen von Amplituden größer 0 und Gruppen mit Amplitude=0, welche sich abwechseln.
Die Gruppen mit Amplitude =0 gelten eher als Trennelemente zwischen den anderen Gruppen. Diese Gruppen, mit erst steigender, dann sinkender Amplitude, nennt man Wellenpakete.
-
Gib dein Wissen über Materiewellen wieder.
TippsBeim Fotoeffekt wird ein Elektron aus dem Valenzband gelöst, indem es ein Photon absorbiert.
LösungIm Bereich der Materiewellen haben wir De Broglie viel zu verdanken.
De Broglies Erkenntnis, wie, dass die Masse frequenzabhängig ist, dass also jedes Teilchen eine Frequenz besitzt, wurde bestätigt durch den Beweis der allgemeinen Relativitätstheorie.
Eine Neuerung war auch, dass die Masse eines Körpers nahe der Lichtgeschwindigkeit größer wird.
Zudem erklärte er die geometrische Optik damit, dass die „Strahlen" senkrecht zu den Wellenfronten verlaufen.
-
Leite die Gruppengeschwindigkeit her.
Tipps$x^{-1}$ bedeutet $\dfrac{1}{x}$.
LösungWenn sich mehrere Schwingungen verschiedener Frequenzen überlagern, entstehen also Wellenpakete mit Gruppengeschwindigkeiten. Aber wie groß ist diese nun? Schließlich besteht sie aus vielen Frequenzen.
Die Gruppengeschwindigkeit ist die Ableitung der Winkelgeschwindigkeit $\omega$ nach der Wellenzahl $k$.
Dabei ist :
$\omega=2\pi\cdot f$
$k=\dfrac{2\pi}{\lambda}$
Haben wir also ein Teilchen mit Impuls
$p=mv$
und Energie
$W=\dfrac{1}{2}\cdot mv^2$,
können wir dieses mit der Energie für Wellen
$W=\dfrac{p^2}{2m}$
in Beziehung setzen.
Mit der Planck'schen Beziehung
$W=hf$
und der De Broglie'schen Beziehung
$P=\dfrac{1}{\lambda}\cdot h$
kann nun für $\omega=2\pi f$ eingesetzt werden:
$\omega=2\pi f=2\pi\dfrac{W}{h}=2\pi \dfrac{p²}{2hm}=\dfrac{2\pi}{2hm}\cdot\dfrac{h^2}{\lambda^2}$.
Da wir nun wissen, wie $k$ aussieht, schreiben wir:
$\omega=\dfrac{hk^2}{4\pi m}$.
Das lässt sich nun nach $k$ ableiten. $k$ wieder einsetzen und kürzen ergibt.
$v=\dfrac{\partial\omega}{\partial k}=2k \dfrac{h}{4\pi m}=2\cdot 2\pi\dfrac{h}{\lambda 4\pi m}$,
also $v=\dfrac{p}{m}$.
Diese Gruppengeschwindigkeit entspricht der Geschwindigkeit für Teilchen. Die Geschwindigkeit der Wellenpakete ist also gleich der des Teilchens.
9.966
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.314
Lernvideos
38.641
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?