Unbestimmtheitsrelation


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Unbestimmtheitsrelation
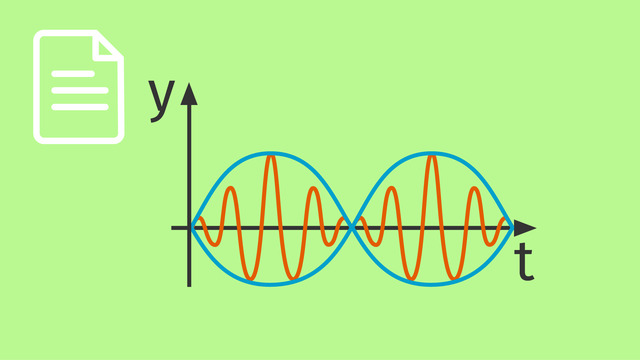
Dieses Video befaßt sich mit der Heisenbergschen Unbestimmtheitsrelation. Ausgangspunkt ist die Modellierung von Teilchenwellen als Überlagerung unendlich vieler Wellen verschiedener Frequenzen. Du erfährst zuerst, wie man zu dieser Modellierung kommt. Anschließend werden die Konsequenzen dieser Art der Darstellung besprochen.
Transkript Unbestimmtheitsrelation
Hallo und herzlich willkommen. Ich erkläre hier kurz ein Modell, was verständlich machen soll, was es mit der Unbestimmtheitsrelation und der Quantentheorie auf sich hat. Du solltest die Interferenzphänomene bei der Überlagerung von Wellen kennen, die Erklärung der akustischen Unschärfe, die Plancksche Beziehung, die De-Broglie-Wellenlänge und über die Quantelung elektromagnetischer Strahlung, genauso wie über die Welleneigenschaften von Teilchen, bescheid wissen. Mit der Bestätigung der Hypothese des Wellencharakters von Teilchen und des Quanten- oder Teilchencharakters elektromagnetischer Wellen, ergibt sich notwendig, dass man Modelle zur Beschreibung konstruieren muss, die kaum noch etwas mit unseren Alltagsvorstellungen verbindet. Eine schmale Brücke haben wir allenfalls mit der Vorstellung von Photonen, genauso wie Elementarteilchen, als sogenannte Wellenpakete, die man eigentlich Paketwellen oder Knotenwellen nennen müsste. Wir wissen ja, dass sich solche Wellenpakete als Resultanten von Welleninterferenz bilden können. Denn wenn man mehrere Wellen verschiedener, nicht zu weit auseinanderliegender Frequenzen überlagert, können Schwebungen entstehen. Und je mehr solcher Wellen aus einem begrenzten Frequenzintervall überlagert werden, desto klarer sind die resultierenden Amplitudenbäuche oder Gruppen voneinander abgesetzt. Und desto weniger sind es auch. Wenn wir dann alle möglichen Frequenzen innerhalb eines begrenzten Intervalls, das heißt also unendlich viele verschiedene überlagern, erhalten wir eine einzelne Gruppe, die sich wie ein vereinzeltes Paket in Raum und Zeit bewegt. Sicher ließe sich dieses Wellenpaket isoliert beschreiben. Mit einer bestimmten Gesamtlänge, einer bestimmten Frequenz, einem bestimmten Amplitudenverlauf und davor und dahinter nun so etwas wie eine Nullwelle. Aber das wäre willkürlich und wir müssten obendrein doch wieder die Bewegung dieses Pakets in Zeit oder Raum mathematisch beschreiben. Wir kommen also gar nicht umhin, die ganze Welle als eine Einheit zu beschreiben. Sie besteht ja nicht aus 3 Stücken, sondern ist eine. Darum hatte ich vorhin gesagt, man sollte diese Wellenform vielleicht eher Paketwelle oder Knotenwelle nennen. Da ihre charakteristische Amplitudenform die einer unendlich langen Geraden mit einer einzigen knotenartigen Verdickung ist. Dann bleibt uns aber nur übrig, die Welle als die Resultante einer Überlagerung unendlich vieler Wellen zu beschreiben, die sie auch ist. Da das Wellenpaket nur dann entsteht, wenn die überlagerten Wellen aus einem begrenzten Frequenzintervall stammen, ergibt sich eine Bedingung für die angeführte Formel. Die Frequenzen liegen in einem symmetrischen Bereich um eine mittlere Frequenz. Vom Phänomen der akustischen Unschärfe wissen wir, das es eine Beziehung zwischen der Breite des Frequenzintervalls und der zeitlichen Erstreckung des Wellenpakets gibt. Je breiter das Frequenzband aus dem die Wellen überlagern, umso kürzer die Dauer der resultierenden Schwingung. Und natürlich umgekehrt. Von Unschärfe muss man ja hier sprechen, weil wir niemals alle Frequenzen der beteiligten Wellen identifizieren könnten. Es sind ja unendlich viele. Das gilt für alle Wellenpakete dieser Art, nicht nur für Schallwellen und es ist der Schlüssel zum Verständnis der Heisenbergschen Unbestimmtheitsrelation. Wir hatten die allgemeinen Beziehungen für die Energiequanten und die Teilchenwellenlänge formuliert, müssen aber nun zugestehen, dass es Vereinfachungen sind. Tatsächlich sind ja nicht nur die Frequenzen unserer knotigen Welle über einen Bereich verschmiert, sondern damit zugleich auch die Größe des Energiequantums und des Impulses des Teilchens. Und natürlich ist das nicht mehr so überraschend, wenn man einmal anerkannt hat, dass die Energie von der Frequenz abhängt. Dann bedeutet eine Zusammensetzung des als Wellenpakets modellierten Objekts aus unendlich vielen Wellen unterschiedlicher Frequenz, dass es unendlich viele verschiedene Energiemengen hat. Und aus der De-Broglie-Formel folgt, dass es dann auch unendlich viele verschiedene Impulsquante hat. Diese Eigentümlichkeit führt schließlich auf das Prinzip der Komplementarität bestimmter Größenpaare in der Quantentheorie. Setzen wir die aus der Akustik bekannte Unschärfenbeziehung allgemein für Welleninterferenzen voraus, erhalten wir mit der Formel für die Unschärfe des Energiequantums einen Ausdruck, an dem ablesbar ist, dass die Bestimmung der Bewegungszeit umso ungenauer wird, je genauer wir das Energiequantum messen. Je kleiner wir die Unschärfe delta W eingrenzen können, desto weiter läuft uns das Unschärfemaß für die Zeit delta t auseinander. Außerdem erhalten wir mit der Formel für die Unschärfe der Impulsgröße einen Ausdruck, an dem ablesbar ist, dass die Bestimmung des Orts umso ungenauer wird, je genauer wir den Impuls messen. Je kleiner wir die Unschärfe delta p eingrenzen, desto weiter läuft das Unbestimmtheitsmaß für den Ort delta s auseinander. Da diese Abhängigkeiten symmetrisch sind, gilt natürlich auch das Umgekehrte. Genaue Ortsbestimmung lässt die Impulsgröße verschwimmen, genaue Zeitmessung die Energiemenge. Wir können also niemals alle messbaren Parameter unseres Objekts zugleich mit gewünschter Genauigkeit bestimmen. Das ist die mit der klassischen Physik nicht mehr erklärbare Konsequenz aus der Heisenbergschen Unbestimmtheitsrelation. Genauere Untersuchung ergibt nun, dass die Grenze noch etwas kleiner ist, als hier angegeben. Wenn nämlich die Hüllkurve dieses Wellenpakets von einer Gaussfunktion beschrieben wird, gilt die Unschärfe delta Omega x delta t = 1/2. Wobei Omega natürlich die Kreisfrequenz Omega = 2 pi x f ist. Damit ergibt sich für die quantenphysikalische Unbestimmtheit eine leicht korrigierte Beziehung. Außerdem ist natürlich selbstverständlich, dass wir mit diesen Beziehungen eine untere Grenze des Unbestimmtheitsmaßes beschreiben. Darum gilt allgemeiner, dass die Produkte der komplementären Größenunschärfen nicht kleiner als h Strich halbe sein können. Ich will mal kurz zusammenfassen. Die beiden Formulierungen der Heisenbergschen Unschärfebeziehungen beruhen auf der Modellierung der Teilchenwellen als Überlagerung unendlich vieler Wellen verschiedener Frequenzen aus einem Intervall. Damit gilt die allgemeine Unschärfebeziehung für Wellenpakete. Die Anwendung dieser Beziehung auf die Plancksche Formel, beziehungsweise die De-Broglie-Formel in angepasster Form, ergibt Ausdrücke die beschreiben, dass je 2 Größen sich in der erreichbaren Maßgenauigkeit komplementär zueinander verhalten. Energie und Zeit beziehungsweise Impuls und Ort. Bei diesen Paaren lassen sich niemals beide zugleich beliebig genau bestimmen. Soviel für diesmal. Viel Vergnügen beim Durchdenken und Verstehen und vielleicht bis zum nächsten Video.
Unbestimmtheitsrelation Übung
-
Gib die Probleme an, die sich aus dem „Welle-Teilchen-Dualismus“ in der Physik der Mikroobjekte ergeben.
TippsDie Untersuchung von Mikroobjekten zeigte, dass sie sich auf zwei üblicherweise nicht vereinbare Arten verhalten können.
LösungEinstein konnte 1905 den äußeren Photoeffekt damit erklären, dass er Licht-Teilchen einführte (Photonen). Zugleich zeigt Licht eindeutig Wellencharakter.
De Broglie behauptete 1924 und Davisson/Germer zeigten 1927 experimentell, dass Elementarteilchen (wie Elektronen) Welleneigenschaften besitzen. Zugleich verhalten sie sich immer wieder wie kompakte Teilchen.
Diese Einheit klassisch unvereinbarer Aspekte wird oft „Welle-Teilchen-Dualismus" genannt.
-
Benenne das Problem, das zur Einführung der Konzeption führt.
TippsWellen sind als in Raum und Zeit sich unendlich ausbreitende Schwingungen modellierbar, Teilchen nur als zusammenhängende Materie begrenzter Abmessungen.
LösungWenn Objekte Welleneigenschaften haben, müssen sie als in Raum und Zeit ausgebreitete Schwingungen dargestellt werden. Wenn Objekte Teilcheneigenschaften haben, müssen sie als geometrisch begrenzte Körper modelliert werden können. Man braucht etwas wie eine in Raum und Zeit begrenzte Schwingung als Modell.
-
Erkläre das Modell, mit dem Wellencharakter und Lokalisierbarkeit zugleich beschrieben werden können.
TippsÜberlagert man Wellen verschiedener Frequenz, ergeben sich manchmal resultierende Wellen mit schwankender Amplitude, die sich zu sog. Schwingungsbäuchen formen.
LösungBei der Überlagerung von Wellen verschiedener Frequenzen aus einem endlich großen Frequenzband ergeben sich Überlagerungsfiguren mit deutlich abgesetzten Wellengruppen. Überlagert man alle Wellen aus dem Kontinuum eines begrenzten Frequenzbandes, bildet sich eine einzelne solche Wellengruppe in Raum und Zeit aus (auch „Wellenknoten" oder „Wellenpaket" genannt).
-
Leite die Heisenberg'sche Relation aus dem Modell ab.
TippsDu musst die Frequenz-Wellenlängen-Beziehung für Wellen und die de-Broglie-Beziehung für Materiewellen für Unschärfe-Bedingungen formulieren, in die Formel der akustischen Umschärfe einsetzen und das Resultat mit der Geschwindigkeits-Zeit-Beziehung vereinfachen.
LösungMit der Ableitung wird sichtbar, wie aus zwei klassisch erklärbaren Voraussetzungen unter Annahme der de-Broglie-Beziehung die nicht-klassische Konsequenz folgt. Man geht am besten folgendermaßen vor:
- Man notiert die Formel für die akustische Unschärfe $\Delta{f} \cdot \Delta{t} = \frac{1}{2}$ (1).
- Man ergänzt die Frequenz-Wellenlängen-Beziehung $f = \frac{v}{\lambda}$ (2a) und die de-Broglie-Beziehung für Materiewellen $p = \frac{h}{\lambda}$ (2b).
- Man formuliert (2) für die Unschärfe-Bedingung um und erhält $\Delta{f} = \frac{v}{\Delta\lambda}$ (3a) bzw. $\Delta{p} = \frac{h}{\Delta\lambda}$ (3b).
- Man setzt (3a) in (1) ein und erhält $\frac{v}{\Delta\lambda} \cdot \Delta{t} = \frac{1}{2}$ (4), das
- man zweckmäßig auf beiden Seiten mit $h$ multipliziert: $\frac{h \cdot v}{\Delta\lambda} \cdot \Delta{t} = \frac{1}{2} \cdot h$ (5), denn das kann man leicht
- mithilfe von (3b) umformen in $\Delta{p} \cdot v \cdot \Delta{t} = \frac{1}{2} \cdot h$ (6), was dann
- mit der Geschwindigkeit-Zeit-Beziehung zu $\Delta{p} \cdot \Delta{x} = \frac{h}{2}$ wird.
-
Nenne die Formel der Unschärfe- oder Unbestimmtheits-Relation.
TippsUnschärfe heißt, die Messwerte bestimmter Größen können nicht punktgenau bestimmt werden, sondern nur annähernd. Man muss mit Werten aus einem gewissen Bereich rechnen.
LösungUnschärfe heißt hier, dass man die Messwerte nicht präzise vorausberechnen kann. Man kann nur gewisse mögliche Intervalle angeben.
Heisenbergs Konzept besagt, dass das Produkt der Intervalle für je zwei sog. komplementäre Größen (Ort und Impuls, Energie und Zeit) nicht kleiner als eine bestimmte untere Grenze werden kann.
-
Begründe die genauere Bestimmung der Unschärfegrenze.
TippsEmpirisch plausibel ist die Annahme, dass sich die Einhüllende der Wellengruppe am besten mit der Gaußschen Normalverteilung beschreiben lässt. Es ist eine in der Natur häufig auftretende Wahrscheinlichkeitsverteilung.
LösungSetzen wir als Form der Hüllkurve der Wellengruppe, mit der unser Wellen-Teilchen-Objekt modelliert wird, die Gauß'sche Normalverteilung über einem mittleren Ort $x=0$ und mit einer Standardabweichung von $\sigma=\frac{1}{\sqrt{2}}$ an, also etwa $f(x)=e^{-x^{2}}$, erhalten wir aus der Lösung der Schrödingergleichung:
$\Delta{\omega}\cdot\Delta{t}=\frac{h}{2}$ oder $\Delta{f}\cdot\Delta{t}=\frac{\hbar}{2}$,
woraus $\Delta{p}\cdot\Delta{x}=\frac{\hbar}{2}$ folgt.
Dass sich die Verteilung von messbaren Größen in der Natur oft einer Gauß'schen Normalverteilung fügt, ist eine empirisch bestätigte Beobachtung.
9.897
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.309
Lernvideos
38.669
Übungen
33.706
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?













Guten Morgen, David Brunner1000,
läßt sich ein auffälliger Punkt nennen, an dem Dein Verständnis strapaziert wird ? Dann könnte ich vielleicht zur Aufklärung verhelfen.
Grüße,
kalo
Wow das hat mich noch mehr verwirrt...