Wellenoptik – Reflexion, Brechung und Interferenz
Die Wellenoptik nutzt das Wellenmodell des Lichts, um Interferenz an dünnen Schichten und am Doppelspalt zu erklären.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Wellenoptik im Alltag
- Wellenmodell des Lichtes
- Reflexion von Wellen
- Brechung von Wellen
- Beugung und Interferenz von elektromagnetischen Wellen
- Der Doppelspaltversuch
- Interferenz an dünnen Schichten
Wellenoptik im Alltag
Hast du dich immer schon einmal gefragt, wo die farbigen Reflexe auf einem Datenträger, einem Ölfleck oder einer Seifenblase stammen? Dies kann dir die Wellenoptik erklären. Die Wellenoptik betrachtet die Ausbreitung des Lichtes als elektromagnetische Welle nach dem Wellenmodell des Lichtes. Mit diesem Modell erklärt die Wellenoptik eine Vielzahl von spannenden Effekten.
Wellenmodell des Lichtes
Das Wellenmodell des Lichtes sagt aus, dass sich Licht wie eine Welle verhält, also genau wie eine Wasserwelle oder Schallwelle. Dabei breitet sich natürlich die Lichtwelle viel schneller aus. Zu diesem Wellenverhalten gehört auch, dass jeder einzelne Punkt einer Wellenfront Ausgangspunkt einer neuen, kreisförmigen Elementarwelle mit gleicher Frequenz und Geschwindigkeit ist. Die Wellenfront ist dabei die Überlagerung dieser Elementarwellen. Erst durch dieses Verhalten ist die Beugung, Reflexion, Brechung und Interferenz des Lichtes erklärbar.
Reflexion von Wellen
Die Reflexion von Wellen nach Christiaan Huygens lässt sich durch das zeitlich versetzte Auftreffen der Wellenfront an der Reflexionsfläche erklären. Durch die Überlagerung der einzelnen Elementarwellen entsteht eine neue Wellenfront. Für die Ausbreitungsrichtung der neuen Wellenfront gilt: Einfallswinkel ist gleich Austrittswinkel. Genau wie auch beim Strahlenmodell des Lichtes.
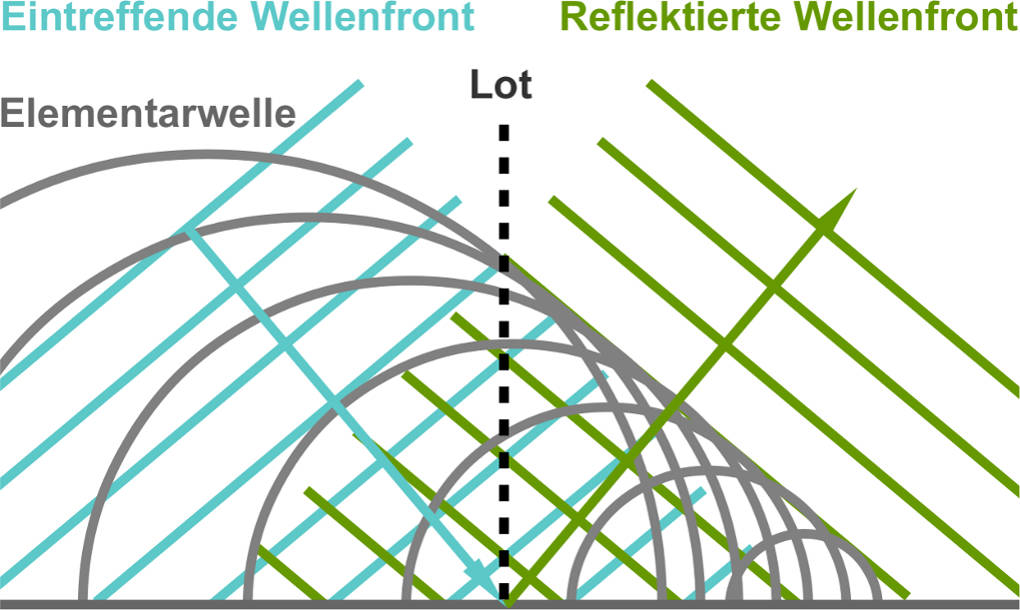
Brechung von Wellen
Auch die Brechung des Lichtes kann mit dem Wellenmodell des Lichtes erklärt werden. Die Ausbreitungsgeschwindigkeit einer Welle hängt vom Medium ab, durch welches sie sich bewegt. Während Schallwellen durch ein dichteres Medium stark beschleunigt werden, wird Licht als elektromagnetische Welle in optisch dichteren Medien verlangsamt. Bei der Brechung müssen wir zwei Fälle unterscheiden. Trifft die Wellenfront unter einem Winkel $\alpha \neq 90^\circ$ auf die Grenzfläche, trifft ein Teil der eingehenden Wellenfront als erstes auf die Grenzfläche. Dieser Teil wird auch früher abgebremst. Durch diese partielle Abbremsung der Welle, ändert diese ihre Ausbreitungsrichtung. Trifft eine Wellenfront jedoch zeitgleich, also gerade, auf die Oberfläche, dann wird sie verlangsamt, ändert jedoch nicht ihre Richtung.
Beugung und Interferenz von elektromagnetischen Wellen
Auch an Kanten entstehen an jedem Punkt der Wellenfront wieder neue Elementarwellen. Diese gelangen sogar in den Schattenraum hinter dem Hindernis. Dies nennt man Beugung von Wellen. Nur wegen diesem Effekt kannst du deine Wohnungsklingel in jedem Raum deines Hauses hören. Die entstehenden Elementarwellen überlagern sich wiederum hinter dem Hindernis und bilden neue lokal begrenzte Wellenfronten aus. Man spricht von Interferenz von Wellen. Diese kann konstruktiv sein, dabei verstärkten sich die Wellen, oder destruktiv, dann schwächen sich die Wellen gegenseitig ab.
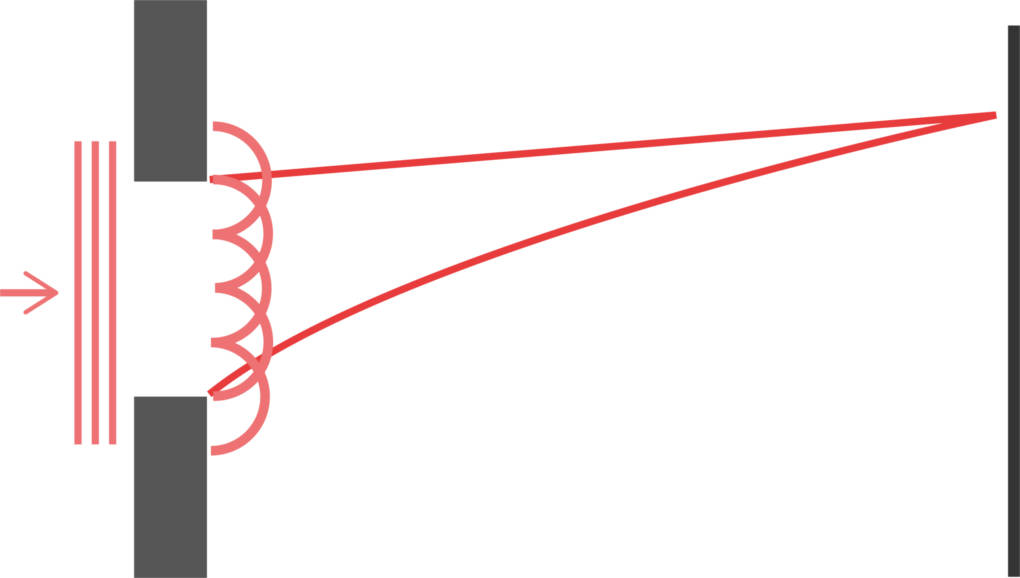
Der Doppelspaltversuch
Ein typisches Beispiel für die Interferenz und Beugung von Wellen ist der Doppelspaltversuch nach Thomas Young. Bei diesem Versuch läuft die kohärente Wellenfront auf zwei Spalte zu, deren Spaltbreite $b$ im Bereich der Wellenlänge $\lambda$ des eingesetzten Lichtes liegt. An diesen feinen Öffnungen tritt Beugung auf. Die entstehenden Elementarwellen an den beiden Öffnungen interferieren miteinander. Durch den kleinen Abstand $d$ der Spalte zueinander, tritt nun ein Gangunterschied bei den Elementarwellen auf. Auf dem Schirm zeigt sich ein Interferenzmuster.
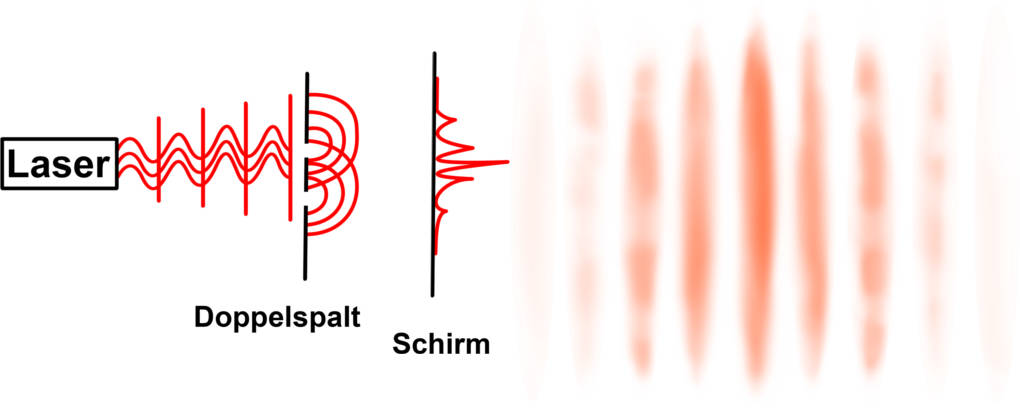
Ist dieser Gangunterschied $\Delta s$ gerade ein Vielfaches der Wellenlänge, tritt hinter dem Spalt ein Maximum durch konstruktive Interferenz auf. Ist der Gangunterschied gerade ein ungradzahliges Vielfaches der halben Wellenlänge, tritt ein Minimum durch destruktive Interferenz auf.
Für ein Maximum $\Delta s=n\cdot \lambda \text{ mit } n=0,1,2,3…$
Für ein Minimum $\Delta s=(n-\frac{1}{2}) \cdot \lambda \text{ mit } n=0,1,2,3…$
Interferenz an dünnen Schichten
Es gibt auch Interferenz an dünnen Schichten. Diese Schichten können die Haut einer Seifenblase, die Oberfläche einer CD oder auch die Glimmerschicht eines Kristalls sein. Trifft nun Licht auf die Oberfläche der Schicht, wird dieses nur partiell von dieser reflektiert. Auch an der Unterseite der Schicht tritt wieder partielle Reflexion auf. Aus einem Lichtstrahl werden nun zwei Lichtstrahlen mit einem Gangunterschied von $\Delta s$.
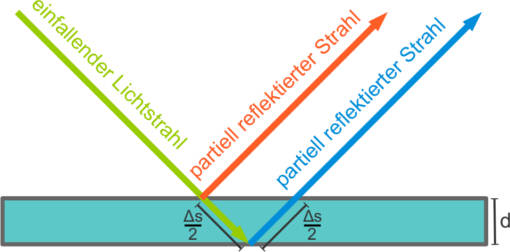
Wenn diese interferieren, zeigt sich auch hier ein Interferenzmuster. Setzt man statt einfarbigem (monochromatischen) Licht, weißes Licht ein, zeigt sich das Farbenspiel wie an der Oberfläche der Seifenblase. Da die Seifenblasenhaut wegen der Schwerkraft unten dicker ist als oben, zeigt sich hier sogar ein bewegtes Farbenspiel.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Wellenoptik – Reflexion, Brechung und Interferenz (8 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Wellenoptik – Reflexion, Brechung und Interferenz (9 Arbeitsblätter)
-
 Strahlenmodell und Wellenmodell der Optik
PDF anzeigen
Strahlenmodell und Wellenmodell der Optik
PDF anzeigen -
 Wellenmodell des Lichts
PDF anzeigen
Wellenmodell des Lichts
PDF anzeigen -
 Reflexion und Brechung einer Welle an der Grenzfläche zweier Medien
PDF anzeigen
Reflexion und Brechung einer Welle an der Grenzfläche zweier Medien
PDF anzeigen -
 Beugung und Interferenz
PDF anzeigen
Beugung und Interferenz
PDF anzeigen -
 Interferenz elektromagnetischer Wellen
PDF anzeigen
Interferenz elektromagnetischer Wellen
PDF anzeigen -
 Beugung und Interferenz von Licht am Doppelspalt
PDF anzeigen
Beugung und Interferenz von Licht am Doppelspalt
PDF anzeigen -
 Interferenz elektromagnetischer Wellen am Beugungsgitter – Übungen
PDF anzeigen
Interferenz elektromagnetischer Wellen am Beugungsgitter – Übungen
PDF anzeigen -
 Interferenz an dünnen Schichten
PDF anzeigen
Interferenz an dünnen Schichten
PDF anzeigen -
 Michelson-Interferometer
PDF anzeigen
Michelson-Interferometer
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie



















