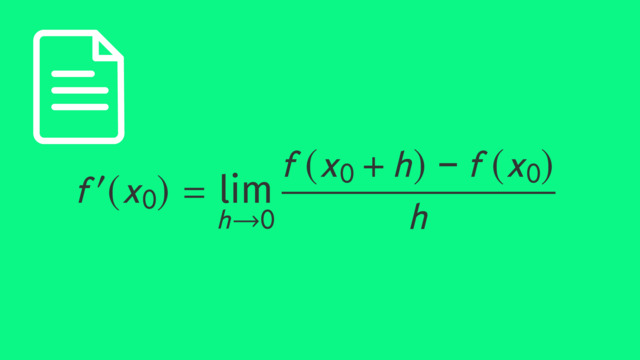Zweite Ableitung
- Was ist die zweite Ableitung?
- Wie wird die zweite Ableitung gebildet?
- Berechnung der zweiten Ableitung – Beispiel
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
5 Minuten verstehen
5 Minuten üben
2 Minuten Fragen stellen
Bereit für eine echte Prüfung?
Lerntext zum Thema Zweite Ableitung
Was ist die zweite Ableitung?
Die Bildung der ersten Ableitung einer Funktion ist bereits bekannt. Diese wird mit $f^\prime(x)$ bezeichnet, nach verschiedenen Regeln gebildet und ist ebenfalls eine Funktion.
Aus diesem Grund kann man von dieser Funktion auch wieder eine Ableitung bilden: Es wird also die Ableitung der ursprünglichen Funktion $f(x)$ abgeleitet. Diese sogenannte „zweite Ableitung“ wäre korrekt ausgedrückt $(f^\prime)^\prime(x)$ – vereinfacht nennt man sie aber $f^{\prime\prime}(x)$ (man sagt „f zwei Strich von $x$“). Da sich hier wieder eine Funktion ergibt, könnte man weitere Ableitungen bilden, die dann entsprechend mit $f^{\prime\prime\prime}(x)$ etc. bezeichnet werden.
Wie wird die zweite Ableitung gebildet?
Die zweite Ableitung wird wie die erste Ableitung abhängig von der vorliegenden Funktion anhand der Ableitungsregeln (u. a. Potenzregel, Faktorregel und Summenregel) bestimmt.
Berechnung der zweiten Ableitung – Beispiel
$f(x) = 3x^{4}+5x^{2}-2x+12 \newline f^\prime (x) = 12x^{3}+10x-2 \newline f^{\prime\prime} (x)= 36x^{2}+10$
Was bedeutet die zweite Ableitung?
Die erste Ableitung bezeichnet die Steigung der ursprünglichen Funktion. Bildet man nun die Ableitung der Ableitung, muss dies im Folgeschluss bedeuten, dass mit der zweiten Ableitung die Steigung der ersten Ableitung – also die Steigung der Steigung – bestimmt wird. Doch was heißt das konkret?
Die zweite Ableitung hilft, das Krümmungsverhalten der Funktion $f(x)$ zu untersuchen, denn sie gibt die Änderung der Steigung an. Mit der Berechnung von $f^{\prime\prime}(x)$ kann bestimmt werden, ob es sich um eine Rechtskrümmung oder eine Linkskrümmung handelt. Ebenfalls kann man mit der zweiten Ableitung – genau wie mit der ersten Ableitung – spezielle, charakteristische Punkte der Funktion bestimmen.
Wendepunkte
Wenn die zweite Ableitung einer Funktion an einer gegebenen Stelle gleich null ist, kann bei dieser Stelle ein Wendepunkt vorliegen. Das Grundprinzip ist hier das gleiche wie bei Extrempunkten und der ersten Ableitung. Wendepunkte sind Punkte, an denen sich die Krümmung des Funktionsgraphen ändert. Er wechselt hier von einer Rechtskrümmung in eine Linkskrümmung oder umgekehrt. Um Wendepunkte zu bestimmen muss also grundsätzlich die zweite Ableitung gleich null gesetzt werden.
Ein Beispiel aus der Praxis – was bedeutet die zweite Ableitung im Sachzusammenhang?
Eine Anwendung der zweiten Ableitung lässt sich in der Physik bzw. im Alltag einer jeden Person finden. Hierbei ist die Rede von der Darstellung des Wegs in Abhängigkeit von der Zeit oder als Frage formuliert:
Welchen Weg haben ein Auto/eine Person/ein Flugzeug zu einem bestimmten Zeitpunkt zurückgelegt?
Dabei bezeichnet $x$ die vergangene Zeit und $f(x)$ den zurückgelegten Weg.
| $x$ | $f(x)$ |
|---|---|
| $\text{Zeit}$ | $\text{Weg}$ |
Daraus lassen sich die Bedeutungen der Ableitung schlussfolgern:
| $f^\prime (x)$ | $f^{\prime\prime}(x)$ |
|---|---|
| $\text{Wegänderung} \rightarrow \text{Geschwindigkeit}$ | $\text{Geschwindigkeitsänderung} \rightarrow \text{Beschleunigung}$ |
Die erste Ableitung stellt also die Änderung des Wegs dar, was im Sachzusammenhang die Geschwindigkeit beschreibt. Die Geschwindigkeitsänderung wiederum (also die zweite Ableitung) bezeichnet man als Beschleunigung.
Folgende Zusammenhänge kann man nun außerdem feststellen:
- Wenn $f^{\prime\prime}(x)<0$ gilt, herrscht eine „negative Beschleunigung“ vor – es wird also gebremst und die Geschwindigkeit nimmt ab: $f^\prime (x)$ fällt.
- Wenn $f^{\prime\prime}(x)>0$ gilt, herrscht eine „positive Beschleunigung“ vor – es wird also beschleunigt und die Geschwindigkeit nimmt zu: $f^\prime (x)$ steigt.
- Wenn $f^{\prime\prime}(x)=0$ gilt, findet keine Beschleunigung statt und die Geschwindigkeit bleibt konstant: $f^{\prime\prime}(x)$ hat ein Maximum, Minimum oder einen Sattelpunkt, denn, wenn anschließend wieder beschleunigt wird, steigt die Geschwindigkeit über diesen Punkt hinaus. Wird anschließend wieder gebremst, fällt die Geschwindigkeit unter diesen Punkt ab.
Zweite Ableitung – Ausblick
Wenn du mehr darüber erfahren möchtest, welche Rolle die zweite Ableitung in der Mathematik spielt, Solltest du dich mit Wendepunkten auseinandersetzen. Potenzielle Wendestellen können berechnet werden, indem die zweite Ableitung gleich null gesetzt wird (notwendige Bedingung für einen Wendepunkt: $f^{\prime\prime}(x)=0$). Außerdem muss die dritte Ableitung ungleich null sein (hinreichende Bedingung für einen Wendepunkt: $f^{\prime\prime}(x)=0$ und $f^{\prime\prime\prime} (x) \neq 0$).
Zweite Ableitung – Zusammenfassung
- An der zweiten Ableitung einer Funktion $f^{\prime\prime}(x)$ lässt sich das Krümmungsverhalten des Funktionsgraphen ablesen.
- Für das Krümmungsverhalten von Funktionsgraphen gilt: $\newline f^{\prime\prime}(x)>0 \rightarrow f~ \text{ist linksgekrümmt} \newline f^{\prime\prime}(x)<0 \rightarrow f~ \text{ist rechtsgekrümmt}$
- Wendepunkte sind die Punkte einer Funktion, an denen die Steigung maximal bzw. minimal ist.
Zweite Ableitung Übung
-
Bestimme die zweite Ableitung.
TippsBestimme zunächst die erste Ableitung. Den erhaltenen Term leitest du nochmal ab.
Lösung$f(x)=10x^5-13x^3+4x+2$
$f^{\prime}(x)=50x^4-39x^2+4$
$f^{\prime\prime}(x)=200x^3-78x$
-
Bennene die Eigenschaften der Ableitungen.
TippsDie Steigung der Steigung ist die Änderung der Steigung.
LösungDie erste Ableitung gibt die Steigung der ursprünglichen Funktion an.
Die Ableitung der Ableitung, also die zweite Ableitung, gibt die Steigung der Steigung bzw. die Krümmung der Funktion an.
Für das Krümmungsverhalten der Funktion gilt:
$f^{\prime\prime}(x)>0 \rightarrow f$ ist linksgekrümmt
$f^{\prime\prime}(x)<0 \rightarrow f$ ist rechtsgekrümmt
-
Beschreibe das Vorgehen zur Bestimmung von Wendepunkten.
TippsDrei Aussagen sind richtig.
LösungUm die Wendepunkte zu bestimmen, geht man in drei Schritten vor.
Zunächst muss man die erste Ableitung gleich null setzen. Die Lösungen dieser Gleichung sind die potenziellen Wendestellen.
An den Wendestellen darf die dritte Ableitung nicht gleich null sein. Also setzt man die potenziellen Wendestellen in die dritte Ableitung ein und prüft, ob das Ergebnis ungleich null ist.
Liegt ein Wendepunkt vor, muss noch die $y$-Koordinate bestimmt werden. Dazu setzt man die Wendestellen in die ursprüngliche Funktion ein.
-
Bestimme den Wendepunkt.
Tipps$f''(x) = 6x - 12$
Eine potenzielle Wendestelle liegt bei $x=2$.
Lösung- Bilde zunächst die ersten drei Ableitungen:
$f'(x) = 3x^2 - 12x + 12$
$f''(x) = 6x - 12$
$f'''(x) = 6$
- Setze dann die zweite Ableitung gleich Null und bestimme die Lösung:
- Setze die potenzielle Wendestelle in die dritte Ableitung ein:
Es liegt eine Wendestelle bei $x=2$ vor.
- Bestimme die $y$-Koordinate durch Einsetzen in die ursprüngliche Funktion.
- Der Wendepunkt hat die Koordinaten $(2\vert 3)$.
-
Gib die Eigenschaft einer Funktion am Wendepunkt an.
TippsWenn du dir vorstellst, mit dem Fahrrad von $-\infty$ bis $+\infty$ auf dem Graphen zu fahren, ist der Wendepunkt der Punkt, an dem du den Lenker wendest, also über die Mitte von einer Seite auf die andere wechselst.
LösungDer Wendepunkt ist der Punkt, an dem dem der Graph der Funktion von einer Linkskrümmung in eine Rechtskrümmung übergeht oder andersherum.
-
Bestimme das Krümmungsverhalten.
TippsBilde die zweite Ableitung und prüfe, ob diese eine Nullstelle besitzt oder ob sie durchgängig das gleiche Vorzeichen hat.
Wenn die zweite Ableitung null ist, liegt keine Krümmung vor.
Lösung- $f(x)=x^2+3x-2$
Du kannst dir auch vorstellen, dass es sich um eine nach oben geöffnete Parabel handelt und wenn du diese mit dem Fahrrad abfährst, würdest du die ganze Zeit nach links lenken.
- $f(x)=-3x^4$
Der Graph ist ähnlich wie eine Parabel geformt und nach unten geöffnet. Wenn du diesen Graphen mit dem Rad abfährst, musst du die ganze Zeit nach rechts lenken.
- $f(x)=0,5x+7$
- $f(x)=x^3$
Der Graph hat einen S-förmigen Verlauf und wollte man entlang des Graphen fahren, müsste man in verschiedene Richtungen lenken.
9.460
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.245
Lernvideos
38.711
Übungen
33.574
Arbeitsblätter
24h
Hilfe von Lehrkräften
Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
