Kreise – Einführung
Mit Kreisen kannst du sehr schöne Muster erzeugen. Weißt du noch, was ein Kreis ist? Hier erfährst du Vieles über Kreise und Kreisfiguren.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Einführung
Zunächst einmal klären wir, was ein Kreis ist. Ein Kreis ist ein zweidimensionales Objekt, das keine Ecken hat. Es besteht aus einem geschlossenen Kreisbogen, der die Eigenschaft hat, dass alle Punkte auf ihm den gleichen Abstand zum Mittelpunkt $M$ haben. Diesen Abstand nennt man Radius oder kurz $r$. 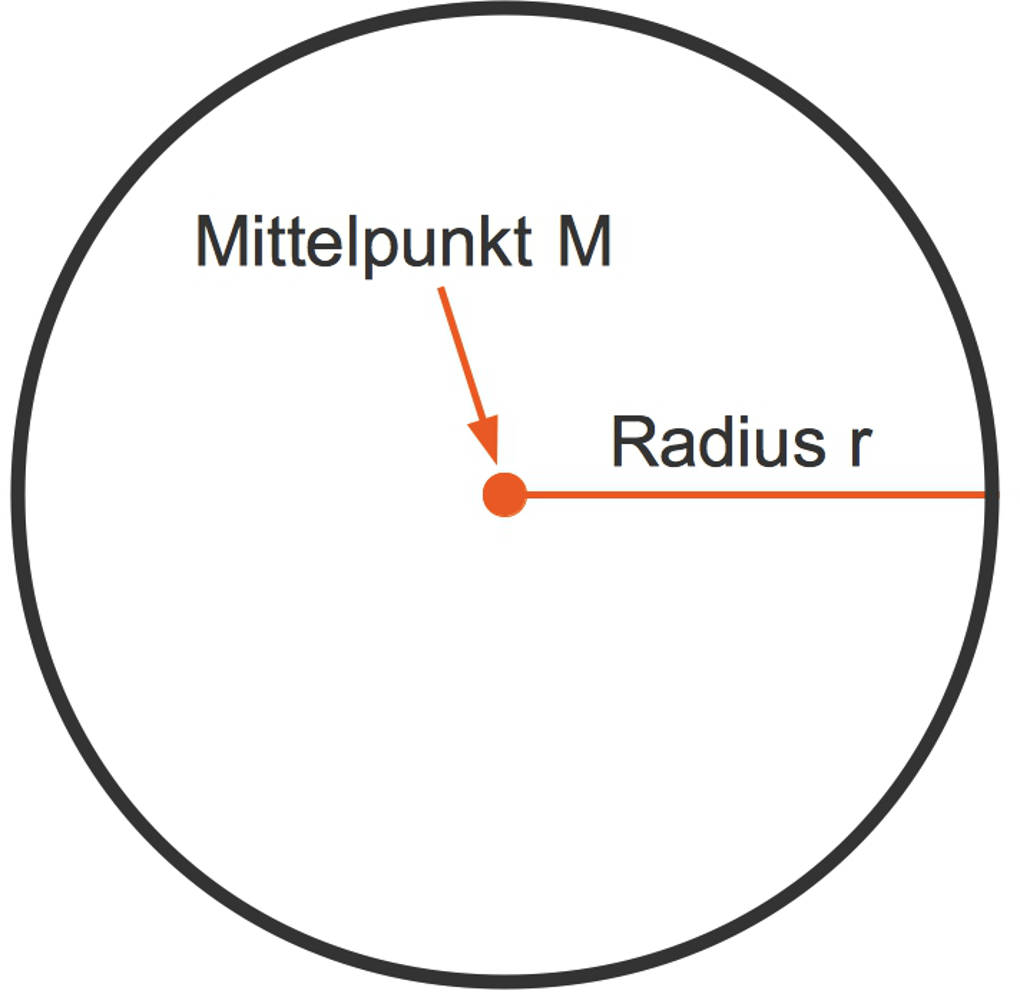
Kreisfiguren (Mandalas)
Der Name Mandala kommt aus dem Indischen und steht für „Kreis“. Eine alte indische Methode, um Konzentration und Ruhe zu finden. Wie zeichnest du ein Mandala? Du benötigst einen Zirkel, um einen Kreis zu zeichnen, sowie ein Geodreieck. Warum einen Zirkel? Na weil ein Mandala eine Kreisfigur ist. Die Konstruktion von Mandalas basiert auf Kreisen, die in gleichen Abständen zueinander in einen Kreis gezeichnet werden. Hier siehst du ein Mandala. Einzelne Flächen sind bereits ausgemalt. Du kannst nun dieses Mandala auf ein Blatt übertragen und auch noch die verbleibenden Flächen ausmalen: 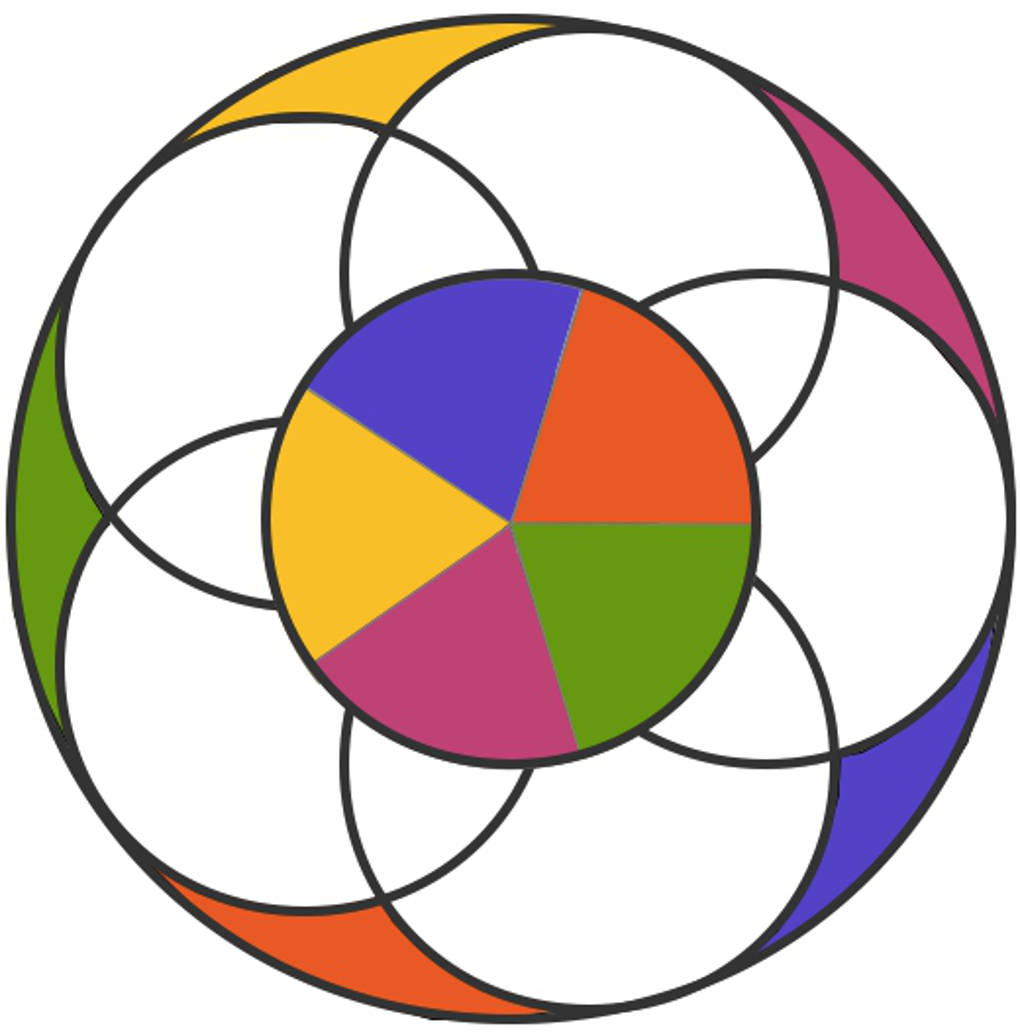
Alle Videos zum Thema
Videos zum Thema
Kreise – Einführung (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kreise – Einführung (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 Kreis – Definition, Begriffe und Konstruktion
Kreis – Definition, Begriffe und Konstruktion
 Kreisfiguren (Mandalas)
Kreisfiguren (Mandalas)









