Das ideale Gas und seine Gesetze

Inhaltsverzeichnis zum Thema

• Was ist ein ideales Gas? - Definition und Überblick
• Das ideale Gasgesetz
• Das Gesetz von Amontons
• Gesetz von Amontons in der Praxis
• Darstellung im Teilchenmodell
• Das Gesetz von Gay-Lussac
• Gesetz von Gay-Lussac in der Praxis
• Darstellung im Teilchenmodell
• Das Gesetz von Boyle-Mariotte
• Das Gesetz von Boyle-Mariotte in der Praxis
• Darstellung im Teilchenmodell

Was ist ein ideales Gas? - Definition und Überblick

In der Natur liegen alle Stoffe in den drei verschiedenen Aggregatzuständen fest, flüssig und gasförmig vor. Gasförmige Stoffe werden als Gase bezeichnet. Beispiele hierfür sind Wasserdampf und Luft, die wiederum ein Gasgemisch aus Stickstoff, Sauerstoff, Kohlenstoffdioxid und diversen Edelgasen wie Helium ist.

Alle Gase sind eigentlich reale Gase mit einer Vielzahl von Eigenschaften, die die Formeln zur exakten physikalischen Beschreibung kompliziert machen. In der Regel kannst du allerdings das Modell des idealen Gases verwenden, das auf folgende Vereinfachungen zurückgreift:

• Ein ideales Gas besteht nicht aus Atomen oder Molekülen sondern aus Punktteilchen ohne räumliche Ausdehnung.

• In einem idealen Gas gibt es keine inelastischen Stöße oder sonstige Wechselwirkungen zwischen den Teilchen. Es gibt lediglich elastische Stöße zwischen zwei Teilchen oder mit der Wand.

• Das ideale Gas verändert nicht seine Stoffmenge $n$ also die Anzahl seiner Gasteilchen $N$. Man spricht von einem geschlossenen System.

Ein ideales Gas gibt es nicht. Verdünnt man ein reales Gas allerdings weit genug, so kann man es recht gut mit dem einfachen idealen Gasgesetz beschreiben. Dieses gibt einen Zusammenhang zwischen den Zustandsgrößen Druck, Temperatur und Volumen an. Die Temperatur eines Gases entspricht im Teilchenmodell der Materie der Bewegungsenergie der Gasteilchen. Je heißer, desto schneller bewegen sich die Teilchen und desto mehr Kraft kann auf die Wände eines Gefäßes übertragen werden. Das Verhältnis zwischen ausgeübter Kraft $F$ und Fläche $A$ hast du schon als Druck kennengelernt.

$p=\frac{F}{A}$

Das ideale Gasgesetz

Ein ideales Gas wird durch die Formel

$\frac{p\cdot V}{T} = \text{const.}$

beschrieben. Das Produkt aus Druck $p$ und Volumen $V$ geteilt durch die Temperatur $T$ ist also eine Konstante (const.). Durch Festhalten einer der drei Zustandsgrößen findet man Zusammenhänge der übrigen beiden Größen und kann so aus dem idealen Gasgesetz weitere Gesetze ableiten.

Das Gesetz von Amontons

Sei nun $V$ ein konstantes Volumen. In der Realität könnte das zum Beispiel eine Druckflasche (Deodorant, Haarspray etc.) oder ein Einmachglas sein. Diese Gefäße sind fest und stabil, ihr Volumen lässt sich ohne Weiteres nicht ändern. In der Formel des idealen Gasgesetzes kannst du nun das Volumen $V$ ignorieren, da es unveränderlich ist, und es bleibt:

$\frac{p}{T}=\text{const.}$

übrig. Der Quotient aus Druck und Temperatur ist also konstant. Diesen Zusammenhang bezeichnet man als das Gesetz von Amontons.

Sinkt die Temperatur von $T_0$ auf $T_1$, so muss auch der Druck von $p_0$ auf $p_1$ sinken und umgekehrt. Du erhältst folglich einen linearen Zusammenhang $p\propto T$ und die Gleichung:

$\frac{p_0}{p_1}=\frac{T_0}{T_1}$.

Gesetz von Amontons in der Praxis

Legt man eine Haarspraydose in die Sonne, so erwärmt sie sich samt Inhalt. Da das Volumen konstant bleibt, erhöht sich auch der Druck. Im schlimmsten Fall kann die Dose deswegen sogar explodieren. Daher sollte man sie auch unbedingt von Wärmequellen fernhalten. Der umgekehrte Fall tritt beispielsweise beim Einmachen von Marmelade ein. Man füllt die fertige Marmelade sehr heiß in ein Einmachglas und verschließt es. Anschließend kühlt der Glasinhalt ab und der Druck sinkt; es bildet sich Unterdruck im Glas und es lässt sich nur schwer wieder öffnen. Dadurch und wegen des Zuckers in der Marmelade sind die Gläser dann lange haltbar.

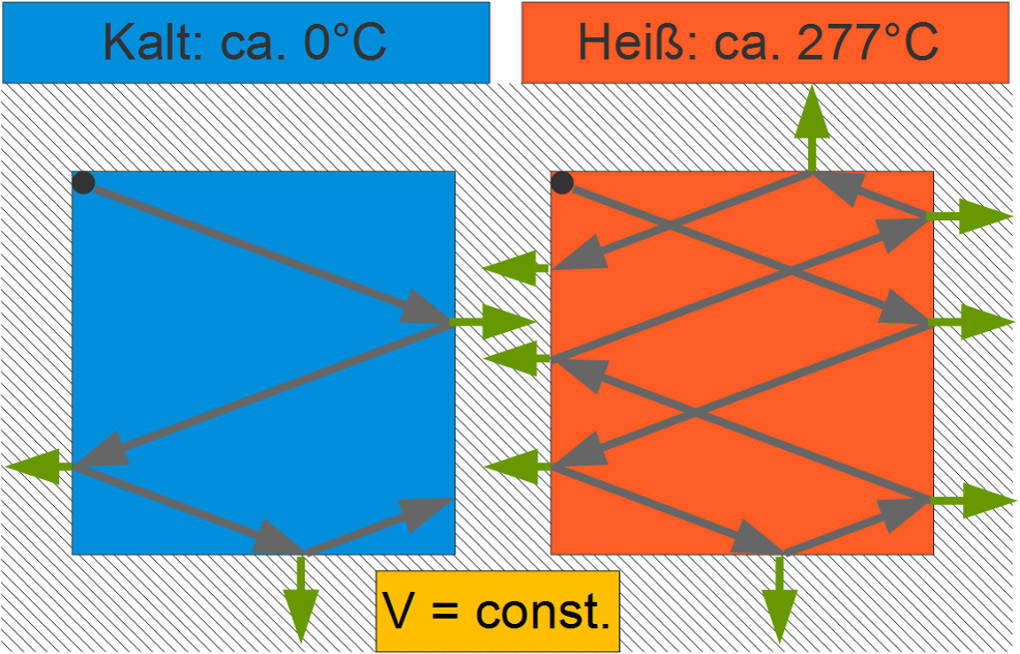
Darstellung im Teilchenmodell

Im Teilchenmodell können schnellere Teilchen in der gleichen Zeit mehr Kraft auf die Gefäßwand ausüben als langsamere Teilchen, da sie statistisch häufiger mit dieser zusammenstoßen und auch bei jedem Stoß mehr Energie Kraft übertragen.

Da das Volumen und damit die Fläche unverändert bleibt, folgt aus der Erhöhung der Kraft ein größerer Druck.

Das Gesetz von Gay-Lussac

Stelle dir nun ein System mit konstantem Druck vor, beispielsweise einen aufgeblasenen Luftballon. Unabhängig von seiner Größe herrscht immer ein Druckgleichgewicht zwischen dem Umgebungsdruck, der versucht, den Luftballon zusammenzudrücken, und dem Druck im Inneren, der versucht, den Luftballon aufzublähen. Der Druck im Luftballon ist stets gleich dem Umgebungsdruck und damit konstant. Im idealen Gasgesetz kannst du nun analog zu oben den konstanten Druck $p$ vernachlässigen und du erhältst:

$\frac{V}{T}=\text{const.}$

Der Quotient aus Volumen und Temperatur ist also ebenfalls konstant und bekannt als das Gesetz von Gay-Lussac.

Gesetz von Gay-Lussac in der Praxis

Steigt die Temperatur im Luftballon von $T_0$ auf $T_1$, wenn man ihn beispielsweise in die Sonne legt, so muss auch sein Volumen größer werden. Der Luftballon bläht sich von $V_0$ auf $V_1$ auf. Die entsprechende Gleichung lautet:

$\frac{T_0}{T_1}=\frac{V_0}{V_1}$.

Darstellung im Teilchenmodell

Im Teilchenmodell können schnelle Teilchen mehr Kraft auf die Luftballonwand ausüben. Da aber gleichzeitig der Luftballon und damit die Fläche wächst, bleibt der Druck konstant.

Das Gesetz von Boyle-Mariotte

Wenn du die Temperatur $T$ eines Systems konstant hältst, kannst du die Temperatur in der Formel des idealen Gases vernachlässigen und es bleibt der Zusammenhang

$p\cdot V=\text{const.}$,

der als das Gesetz von Boyle-Mariotte bekannt ist. Das Produkt aus dem Druck und dem Volumen ist konstant. Das bedeutet, dass sich der Druck von $p_0$ auf $p_1$ erhöht, wenn man das Volumen von $V_0$ auf $V_1$ verringert und umgekehrt. Du erhältst einen umgekehrt proportionalen Zusammenhang $V\propto \frac1{p}$ und die Gleichung:

$\frac{p_0}{p_1}=\frac{V_1}{V_0}$.

Das Gesetz von Boyle-Mariotte in der Praxis

Eine mit Wasser gefüllte versiegelte Spritze ist ein gutes Beispiel. Versuchst du den Kolben hineinzudrücken, also das Volumen zu verringern, so erhöht sich der Druck. Wäre die Spritze offen, so würde nun das Wasser herausspritzen. Dass dabei die Temperatur konstant bleibt, ist gewährleistet, wenn man möglichst langsam drückt. Man bezeichnet dies auch als adiabatische Volumenänderung.

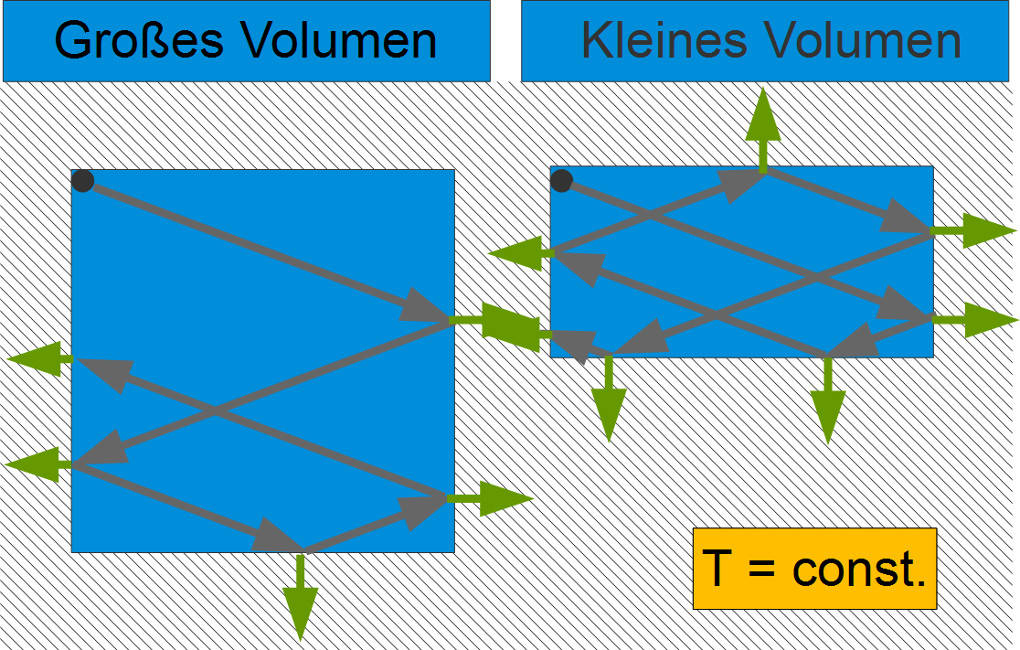
Darstellung im Teilchenmodell

Im Teilchenmodell bleibt die Bewegungsenergie der Teilchen während des gesamten Vorgangs gleich, da wir die Temperatur unverändert lassen. Verringert man dabei das Volumen, folgt daraus, dass die Teilchen viel häufiger miteinander und der Wand zusammenstoßen, also mehr Kraft auf die Wand wirkt. Gleichzeitig verringert sich die Fläche und folglich steigt der Druck.