Differenzialgleichungen der mechanischen Schwingungen
Harmonische, gedämpfte und erzwungene Schwingungen können durch Schwingungsgleichungen, deren Lösungen Schwingungsfunktionen sind, beschrieben werden.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Der harmonische Oszillator
- Gedämpfte und erzwungene Schwingungen
- Schwingungen berechnen
- Schwingungsgleichung
- Schwingungsfunktion
Der harmonische Oszillator
Du kennst bereits mechanische Schwingungen und ihre Grundgrößen. Es wirkt dabei eine rücktreibende Kraft. Wenn nur diese Kraft wirkt, dann wird von einer harmonischen Schwingung gesprochen.
 Die Schwingung müsste dann wegen der Energieerhaltung unendlich weitergehen.
Doch wenn du auf einer Schaukel ganz ruhig sitzt und keinen Schwung holst, dann schwingst du mit jeder Schwingung weniger hoch. Wie kann das sein? Du siehst, es gibt noch weitere Faktoren, die eine Schwingung beeinflussen.
Die Schwingung müsste dann wegen der Energieerhaltung unendlich weitergehen.
Doch wenn du auf einer Schaukel ganz ruhig sitzt und keinen Schwung holst, dann schwingst du mit jeder Schwingung weniger hoch. Wie kann das sein? Du siehst, es gibt noch weitere Faktoren, die eine Schwingung beeinflussen.
Gedämpfte und erzwungene Schwingungen
Du hast bereits etwas zu erzwungenen Schwingungen gelernt. Das sind Schwingungen, die immer wieder von außen angeregt werden. Wir haben auch festgestellt, dass eine alltägliche Schwingung nicht unendlich lang gleich bleibt. Es wirkt in der Realität immer eine Kraft, die der Schwingung entgegenwirkt: Die Reibung. Beim Schaukeln ist dies die Reibung in der Luft, der Luftwiderstand. Somit wird die Schwingung immer schwächer. Es handelt sich um eine gedämpfte Schwingung.
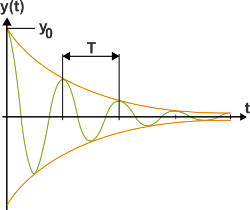
Diese beschreibt wie die harmonische Schwingung einen sinusförmigen Zeitverlauf, dessen Amplitude jedoch immer kleiner wird.
Schwingungen berechnen
Du weißt bereits, dass für eine harmonische Schwingung Energieerhaltung gilt und diese Schwingung einen sinusförmigen Zeitverlauf hat. Doch wie so oft reicht uns die qualitative Beschreibung nicht. Wir wollen sie auch berechnen können.
Schwingungsgleichung
Die Gesamtkraft die auf einen Körper wirkt, wird durch $F=m \cdot a = m \cdot \ddot y$ beschrieben. Denn die Beschleunigung $a$ entspricht der zweiten zeitlichen Ableitung des Weges $y$.
Im Fall einer gedämpften Schwingung setzt sich die Gesamtkraft aus zwei Komponenten zusammen:
- Die Dämpfung, sie kann durch die Kraft $F_D = - \beta \cdot v = - \beta \cdot \dot y$ beschrieben werden. $\beta$ entspricht dem Dämpfungsfaktor.
- Die Federkraft, diese wird nach dem Hook'schen Gesetz durch $F_H=-k \cdot y$ beschrieben.
Es gilt dann insgesamt:
$F= m \cdot \ddot y=- \beta \dot y- k \cdot y$ .
Etwas umgestellt folgt für die Schwingungsgleichung
$0=m \cdot \ddot y+ \beta \cdot \dot y+k \cdot y$.
Dies ist eine Differentialgleichung zweiter Ordnung, denn neben $y$ sind auch die erste und zweite zeitliche Ableitung enthalten.
Im Falle einer harmonischen Schwingung fällt die dämpfende Kraft einfach weg.
$0=m \cdot \ddot y+k \cdot y$ .
Bei einer erzwungenen harmonischen Schwingung wirkt noch eine periodische äußere Kraft auf den Körper ein. Für die Schwingungsgleichung folgt dann:
$m \cdot \ddot y+ k \cdot y = F_a \cdot \cos{(\omega_a \cdot t)}$ .
Dabei ist $\omega_a$ die Kreisfrequenz des Erregers.
Schwingungsfunktion
Die Schwingungsfunktion ist eine Lösung der Schwingungsgleichung. Je nachdem, ob es sich um eine harmonische oder eine gedämpfte Schwingung handelt, folgen hier unterschiedliche Ergebnisse:
Für die Schwingungsfunktion der harmonischen Schwingung gilt:
$y(t)=A \cdot \sin{(\omega \cdot t + \phi)}$.
Für die gedämpfte Schwingung gilt:
$y(t)=A \cdot e^{-\delta \cdot t} \cdot \sin{(\omega\cdot t + \phi)}$.
Dieser unterscheidet sich dadurch von der Lösung der harmonischen Schwingung, dass auch der Dämpfungsfaktor beachtet wird.
Durch zweimaliges Ableiten und Einsetzen in die entsprechende Differentialgleichung kannst du überprüfen, dass die Ansätze die Schwingungsgleichung lösen.
Energie von harmonischen Schwingungen
Für eine harmonische Schwingung gilt die Energieerhaltung. Diese besagt, dass die Gesamtenergie als Summe der Einzelenergien immer konstant bleibt. Die kinetische und die potentielle Energie werden ständig ineinander umgewandelt.
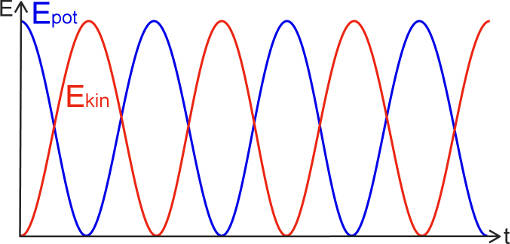
Für die kinetische Energie gilt:
$E_{kin} = \frac{1}{2} \cdot m \cdot v^2 = \frac{1}{2} \cdot m \cdot \dot y$ .
Für die potentielle Energie, hier die Federenergie gilt:
$E_{pot}=\frac{1}{2} \cdot k \cdot y^2$.
Es ist möglich, mithilfe der Schwingungsfunktion eine Gleichung für die Gesamtenergie zu finden:
$E=\frac{1}{2} \cdot k \cdot A^2$ .
Überlagerung harmonischer Schwingungen
Es kann die *Überlagerung harmonischer Schwingungen betrachtet werden. Dabei entsteht eine resultierende Schwingung. Diese ist abhängig von Frequenz und Phasenverschiebung der überlagernden Schwingungen.
Bei gleicher Frequenz ergibt sich als resultierende wieder einer harmonische Schwingung. Diese ergibt sich durch Addition der einzelnen Schwingungen, wobei das Vorzeichen der jeweiligen Auslenkung beachtet werden muss.
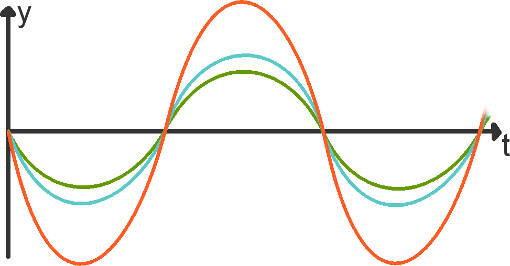
Bei unterschiedlichen Frequenzen kann die resultierende durch punktweise Addition der Auslenkungen erhalten werden. Sie ist in diesem Fall aber nicht harmonisch.
Gekoppelte Schwinger
Als gekoppelte Schwinger werden Pendel bezeichnet, zwischen denen ein Energieaustausch stattfinden kann. Sie werden durch eine Feder miteinander verbunden.
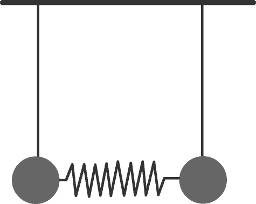
Je nachdem, wie die Pendel am Anfang ausgelenkt werden, folgen drei Möglichkeiten:
- Sie schwingen mit gleicher Amplitude und gleicher Phase (Gleichsinnig).
- Sie schwingen mit gleich großer Amplitude, aber in Gegenphase (Gegensinnig).
- Die Schwingungsenergie wandert zwischen den Pendeln hin und her. Hat eines die maximale Energie, dann steht das andere still (Schwebungsfall).
Alle Videos zum Thema
Videos zum Thema
Differenzialgleichungen der mechanischen Schwingungen (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Differenzialgleichungen der mechanischen Schwingungen (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie








 Mechanische Schwingung
Mechanische Schwingung
 Harmonische mechanische Schwingung
Harmonische mechanische Schwingung
 Energie eines harmonischen Oszillators
Energie eines harmonischen Oszillators
 Mathematische Beschreibung des Federpendels
Mathematische Beschreibung des Federpendels
 Erzwungene mechanische Schwingung
Erzwungene mechanische Schwingung









