Elektromagnetische Induktion

Inhaltsverzeichnis zum Thema

• Was ist Induktion?
• Wie funktioniert elektromagnetische Induktion?
  • Induktionsspannung durch Bewegung
  • Induktionsspannung durch Feldänderung
• Induktionsgesetz
  • Vereinfachung des Induktionsgesetzes in der Schule
• Lenz’sche Regel und ihre Bedeutung für die Induktion
• Selbstinduktion einer Spule
• Elektromagnetische Induktion im Alltag
  • Induktion durch Bewegung: Die Wirbelstrombremse
  • Induktion durch Bewegung: Der Generator
  • Induktion durch Feldänderung: Der Induktionsherds
  • Anwendung der Lenz’schen Regel auf eine Spule
  • Selbstinduktion: Der Transformator

Was ist Induktion?

Bei der elektromagnetischen Induktion handelt es sich um ein Phänomen, bei dem

• die Bewegung eines Leiters durch ein homogenes Magnetfeld oder
• die Änderung des vom Leiter umschlossenen Magnetfeldes

eine elektrische Spannung erzeugen. Durch die elektrische Induktion kann also eine Spannung in einem Stromkreis ohne eigene Spannungsquelle induziert werden. Diese Spannung wird als Induktionsspannung bezeichnet.

Wie funktioniert elektromagnetische Induktion?

Induktionsspannung durch Bewegung

Wird eine Leiterschleife in einem zeitlich konstanten Magnetfeld bewegt und somit ihre vom Magnetfeld durchsetzte Fläche geändert, so kann man zwischen den Enden des Leiters eine Spannung, nämlich die Induktionsspannung messen. Man kann aber auch eine Leiterschleife in einem Magnetfeld enger ziehen, um so die durchsetzte Fläche zu verkleinern. Auch dann misst man zwischen den Enden des Leiters eine Spannung.

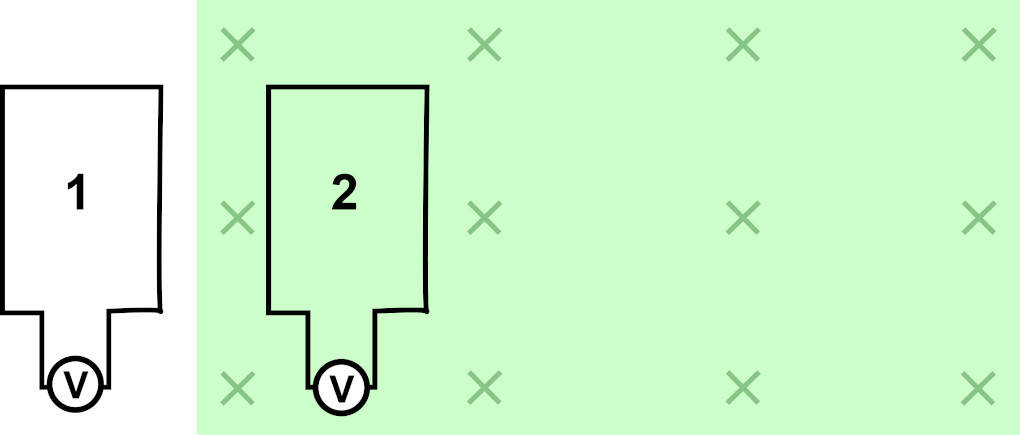
Dieser Vorgang heißt elektromagnetische Induktion und die Spannung wird als Induktionsspannung bezeichnet. Der Betrag der induzierten Spannung hängt dann von der Änderungsgeschwindigkeit der wirksamen Fläche ab. Die wirksame Fläche ist in diesem Fall die vom homogenen Magnetfeld durchsetzte Fläche der Leiterschleife.

Beachte: Es entsteht nur eine Induktionsspannung durch Bewegung, also beim Ändern der Fläche. Sobald sich die Schleife komplett im Magnetfeld befindet oder du ihre Größe nicht mehr änderst, wird die Induktionsspannung gleich Null.

Induktionsspannung durch Feldänderung

Elektromagnetische Induktion können wir auch beobachten, wenn sich das von einer Leiterschleife umfasste magnetische Feld zeitlich ändert. Das Magnetfeld kann man zeitlich ändern, indem man einen Permanentmagneten in eine Leiterschleife oder Spule hinein bewegt. Dabei hängt der Betrag der induzierten Spannung von der Änderungsgeschwindigkeit der magnetischen Flussdichte ab.

Beachte: Es entsteht nur eine Induktionsspannung durch Feldänderung, also solange sich das von der Leiterschleife umschlossene Magnetfeld ändert. Sobald das von der Leiterschleife umschlossene Magnetfeld gleich bleibt, wird die Induktionsspannung gleich Null.

Induktionsgesetz

In einer Leiterschleife oder Spule wird eine Spannung induziert, solange sich das Magnetfeld, das die Fläche der Leiterschleife oder Spule durchsetzt, zeitlich ändert. Das Maß für das Magnetfeld, das die Fläche einer Leiterschleife oder Spule durchsetzt, ist der magnetische Fluss $\phi$ und ist wie folgt definiert:

$\phi=\vec{B}\cdot \vec{A}$

Dabei ist $B$ die magnetische Flussdichte und $A$ die wirksame Fläche. Damit kann die zeitliche Änderung des Magnetfeldes, das die Fläche der Leiterschleife oder Spule durchsetzt, durch die zeitliche Änderung

• der wirksamen Fläche oder
• der magnetischen Flussdichte

realisiert werden. Der Betrag der Induktionsspannung ist von der Schnelligkeit und der Stärke dieser Änderung abhängig. Davon ausgehend kann man wie Michael Faraday das Induktionsgesetz ableiten.

Für eine einzelne Leiterschleife gilt:

$U_\text{i}=-\dfrac{\text{d}\Phi}{\text{d}t}$

Für eine Spule wird mit der Windungszahl $N$ multipliziert:

$U_\text{i}=-N\cdot \dfrac{\text{d}\Phi}{\text{d}t}$

Eine Induktionsspannung $U_\text{i}$ wird folglich durch einen zeitlich veränderlichen magnetischen Fluss $\frac{\text{d}\Phi}{\text{d}t}$ erzeugt und ist proportional zur Anzahl der Leiterschleifen $N$. Warum dort außerdem ein Minuszeichen steht, wirst du in dem Abschnitt zur Lenzschen Regel erfahren.

Du siehst an den Gleichungen, dass du eine Induktionsspannung an den Enden einer Leiterschleife erzeugen kannst, wenn du die Fläche ($\dot{\vec{A}}$), die vom Magnetfeld durchsetzt ist, änderst oder eben jenes Magnetfeld ($\dot{\vec{B}}$) selbst.

Insbesondere bedeutet dies, dass die induzierte Spannung gleich Null ist, es also keine Induktionsspannung gibt, wenn der magnetische Fluss konstant ist. Zur Erinnerung: Die Ableitung einer Konstante ist gleich Null.

Vereinfachung des Induktionsgesetzes in der Schule

Für ein homogenes Magnetfeld ($\vec{B} = \text{konst.}$ und $\vec{B} \perp \vec{A}$) kannst du den magnetischen Fluss durch deren Skalarprodukt ausdrücken:

$\Phi=\vec{B}\cdot\vec{A}=B\cdot A$

Die zeitliche Ableitung oder Änderung des magnetischen Flusses entspricht dann:

$\dfrac{\text{d}\Phi}{\text{d}t}=\dot{\Phi}=\dot{(\vec{B}\cdot\vec{A})}=\dot{\vec{B}}\vec{A}+\vec{B}\dot{\vec{A}}$

Die Schreibweise $\dot{\Phi}$ ist kürzer und damit übersichtlicher. Beide Schreibweisen sind aber gleichwertig, verwende bitte die Schreibweise aus deinem Unterricht.

Lenz’sche Regel und ihre Bedeutung für die Induktion

Wie für alle Prozesse in abgeschlossenen Systemen gilt auch für Induktionsvorgänge die Energieerhaltung:

• Eine Leiterschleife wird im zeitlich konstanten Magnetfeld bewegt und so eine Spannung induziert. Damit wird ein Induktionsstrom hervorgerufen. Dieser ist so gerichtet, dass er eine der Bewegungsrichtung entgegengesetzte Kraft hervorruft. Die mechanische Energie wird in elektrische Energie umgewandelt.
• Bei zeitlicher Änderung des von einer Spule umfassten magnetischen Feldes wird Spannung induziert. Damit wird ein Induktionsstrom hervorgerufen. Dieser ist so gerichtet, dass er ein der Verstärkung des magnetischen Flusses entgegenwirkendes Magnetfeld hervorruft. Die Energie des magnetischen Feldes wird in elektrische Energie umgewandelt.

Die Lenzsche Regel besagt:

„Die Induktionsspannung ist immer der Ursache ihrer Entstehung entgegen gerichtet.“ (Minuszeichen)

Dies ist eine Folgerung aus der Energieerhaltung. Vereinfacht würde man sagen:

Würde die Lenz’sche Regel nicht gelten, würde sich durch gegenseitige Induktion ein elektrischer Strom immer weiter verstärken und wir würden praktisch elektrische Energie erzeugen. Da jedoch Energie weder erzeugt noch vernichtet werden kann, muss die Lenz’sche Regel gelten.

Selbstinduktion einer Spule

Dieses Phänomen bezeichnet man auch als Selbstinduktion einer Spule, also die Induktionswirkung eines stromdurchflossenen Leiters auf sich selbst. Die Induktivität $L$ ist das Verhältnis zwischen induzierter Spannung $U_\text{i}$ und der Änderung der Stromstärke $\dot{I}$:

$L=\frac{-U_\text{i}}{\dot{I}}=N\cdot\frac{\dot{\Phi}}{\dot{I}}$

Speziell für die lange Spule gilt:

$L=\mu\cdot\frac{A}{l}\cdot N^2$

Die Induktivität einer Spule ist abhängig von der Fläche $A$, der Länge $l$ und der Windungszahl $N$ und damit von ihrer Bauform. Die magnetische Permeabilität $\mu$ ist eine Naturkonstante.

Elektromagnetische Induktion im Alltag

Induktion durch Bewegung: Die Wirbelstrombremse

Schauen wir uns nun etwas genauer an, was passiert, wenn man einen Leiter in ein Magnetfeld und wieder hinausbewegt. In einem Leiter gibt es frei bewegliche Elektronen. Bewegst du den Leiter nun in das Magnetfeld eines Permanentmagneten, so wird eine Spannung induziert, die die Elektronen antreibt. Es entsteht ein Wirbelstrom, der wiederum selbst ein Magnetfeld erzeugt, das nach der Lenz'schen Regel dem Feld des Permanentmagneten entgegen gerichtet ist. Die beiden Felder stoßen sich ab und dadurch wird die Bewegung des Leiters in das Magnetfeld gebremst.

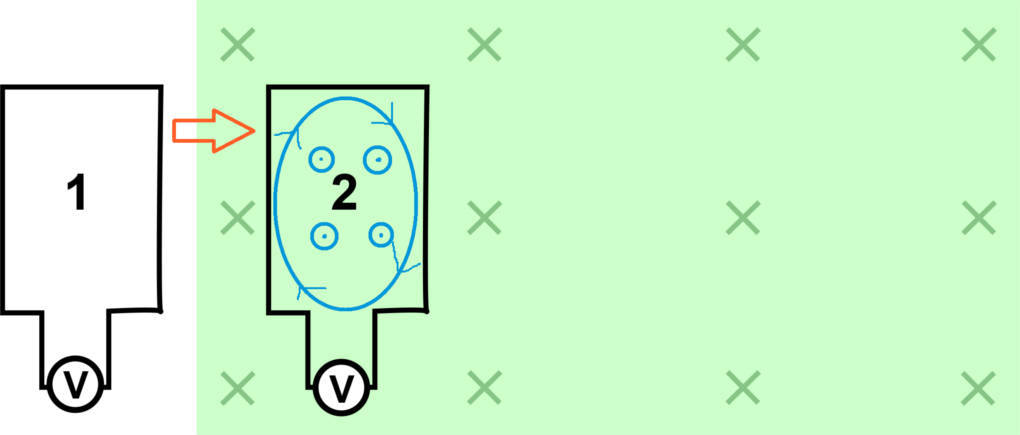
Befindet sich der Leiter mit seiner ganzen Fläche innerhalb des Magnetfeldes, wird die Induktionsspannung gleich Null. Bewegst du nun den Leiter weiter, verlässt er das Magnetfeld wieder. Beim Verlassen des Magnetfeldes wird die Richtung des Wirbelstroms umgekehrt und ein Magnetfeld erzeugt, das in dieselbe Richtung wie das des Permanentmagneten zeigt. Dadurch wird der Leiter angezogen und somit ebenfalls gebremst. Beide Effekte sorgen also für eine Abbremsung des bewegten Leiters aufgrund der induzierten Wirbelströme. Anwendung findet dieses Prinzip in Form einer Wirbelstrombremse bei Zügen.

Induktion durch Bewegung: Der Generator

Der magnetische Fluss ist das Skalarprodukt der Flussdichte und der durchsetzten Fläche und damit abhängig vom Winkel zwischen ihnen. Auch das Drehen einer Leiterschleife in einem Magnetfeld führt somit zu einer Induktionsspannung, da sich der Winkel permanent ändert. Du kannst also mechanische Bewegungsenergie in elektrische Energie umwandeln. Das ist die Umkehrung eines Elektromotors und entspricht der Funktionsweise eines Generators.

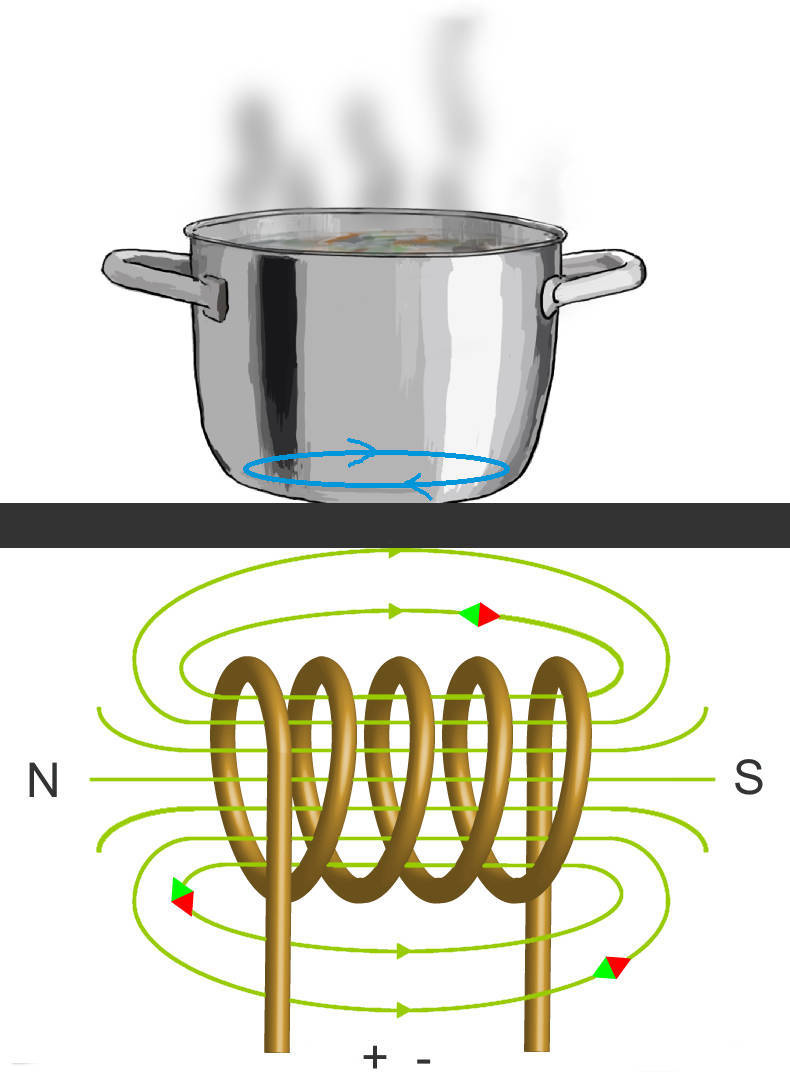
Induktion durch Feldänderung: Der Induktionsherds

Unterhalb der Kochplatte eines Induktionsherds befindet sich eine Spule, die an einer Wechselspannungsquelle angeschlossen ist. Das Vorzeichen der angelegten Spannung kehrt sich also ständig um und infolgedessen auch der Stromfluss durch die Spule. Fließt ein Wechselstrom durch eine Spule, so wird ein zeitlich veränderliches Magnetfeld bzw. ein magnetischer Fluss erzeugt. Aufgrund der elektromagnetischen Induktion bildet sich daher ein Wirbelstrom in dem metallenen Topf auf dem Herd. Dieser hat einen ohmschen Widerstand, sodass schließlich durch die Wirbelströme Wärme entsteht, die du zum Kochen nutzen kannst.

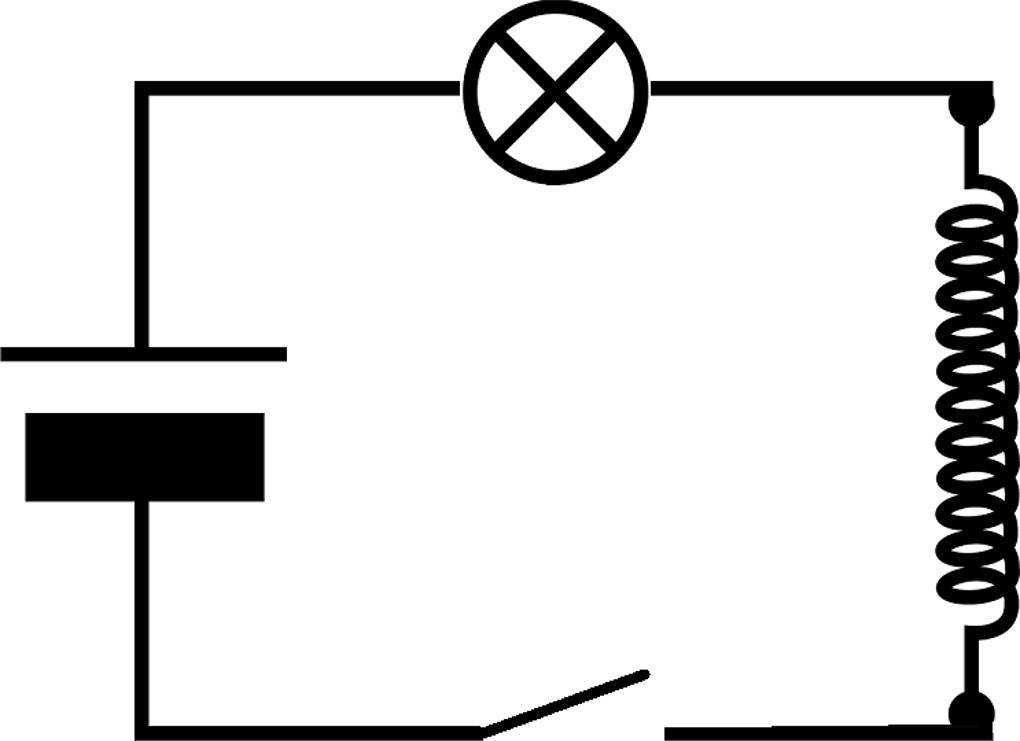
Anwendung der Lenz’schen Regel auf eine Spule

Stell dir eine Spule in einem Schaltkreis mit Schalter vor. Legst du den Schalter um, kann ein Strom $I$ durch die Spule fließen und erzeugt ein homogenes Magnetfeld in ihrem Inneren. Das sich aufbauende Magnetfeld ($\dot{\vec{B}}$) erzeugt nun nach dem allgemeinen Induktionsgesetz eine Induktionsspannung in den Leiterschleifen der Spule. Dies zieht einen Induktionsstrom nach sich, der aufgrund der Lenz'schen Regel ihrer Ursache, also dem Anwachsen des Stromes in der Spule, entgegen gerichtet ist. Der Strom erreicht daher nicht sofort seine volle Stärke und das Magnetfeld entsteht daher nicht instantan, sondern kann sich erst mit der Zeit vollständig aufbauen. Befindet sich zusätzlich eine Glühbirne im Schaltkreis, so wirst du erkennen, dass sie nur allmählich heller wird. Schaltest du den Strom wieder aus, wird die Glühbirne nicht sofort ausgehen, sondern allmählich dunkler werden.

Selbstinduktion: Der Transformator

Die Abhängigkeit der Induktivität einer Spule von ihrer Windungszahl macht man sich bei einem Transformator zu Nutze. Ein Transformator wird verwendet, um elektrische Wechselspannungen umzuwandeln. Dazu wird beispielsweise ein Eisenkern mit zwei Spulen umwickelt, die sich nur in der Anzahl ihrer Windungen ($N_1$, $N_2$) unterscheiden. Nun kannst du an eine der Spulen eine Wechselspannung anlegen. Diese erzeugt ein veränderliches Magnetfeld im Eisenkern, welches wiederum eine Wechselspannung in der zweiten Spule induziert. Hat die zweite Spule weniger Windungen ($N_2 < N_1$), so ist auch der Betrag der induzierten Spannung kleiner. In der Praxis wird mit einem Transformator die Hochspannung der Überlandleitungen in Niedrigspannung des Haushalts umgewandelt.