Differenzialgleichungen der mechanischen Wellen

Inhaltsverzeichnis zum Thema

• Was sind mechanische Wellen?
• Gleichung der harmonischen Welle
• Was sind Differenzialgleichungen?
• Die Wellengleichung

Was sind mechanische Wellen?

Mechanische Schwingungen sind sich wiederholende, periodische Bewegungen eines Körpers oder Teilchen um seine Ruhelage. Überträgt der Körper bzw. das Teilchen dabei Energie an benachbarte Materie und setzt sich dieser Vorgang wie beim Domino-Effekt fort, so entsteht eine mechanische Welle.

Die Ausbreitung solcher Wellen geschieht dabei nach dem sogenannten Huygens’schen Prinzip und benötigt immer ein Medium, das aus gekoppelten Teilchen besteht, wie z. B. Flüssigkeiten oder Luft. Schallwellen, Wellen im Wasser oder auch Erdbeben sind mechanische Wellen.

Stell dir ein Stadion vor. Tausende Menschen bewegen sich auf ihren Plätzen. Das kann ziemlich chaotisch aussehen wie ein riesiger Ameisenhaufen! Doch plötzlich beginnt eine La-Ola-Welle. Dadurch, dass sich die einzelnen Menschen zeitversetzt erheben und wieder setzten, entsteht der Eindruck einer fließenden Welle. So ähnlich kannst du dir das auch mit mechanischen Wellen vorstellen.

Um Wellen zeitlich und örtlich berechnen zu können, wird ein mathematisches Modell benötigt. Doch wie lässt sich so eine Welle darstellen?

Gleichung der harmonischen Welle

Zunächst sieh dir eine Welle zu einer bestimmten Zeit $t_0$ an. Sie kann mit einer Sinusfunktion beschrieben werden und besitzt bestimmte Kenngrößen. Die Auslenkung nach oben und nach unten wird als Amplitude $A$ bezeichnet. Die Wellenlänge $\lambda$ bestimmt, ob und wie die Sinuskurve in x-Richtung gestaucht oder gestreckt wird.

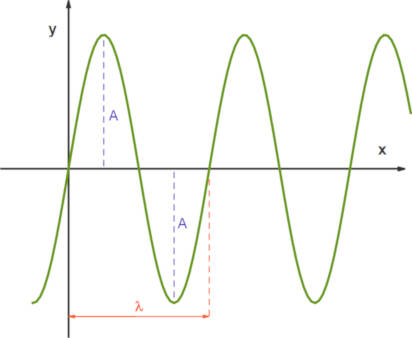
Diese Streckung $b$ kannst du mit folgender Formel berechnen:

$ |b|=\frac{2\cdot \pi}{\lambda} $

Mit diesen Informationen lässt sich die Sinusfunktion aufstellen:

$ f(x) = A\cdot \sin(\frac{2\cdot \pi}{\lambda}\cdot x) $

Diese eindimensionale Welle soll sich nun mit einer konstanten Ausbreitungsgeschwindigkeit $v$ nach rechts bewegen (verschieben). Die horizontale Verschiebung $c(t)$ der Sinuskurve hängt also von der Zeit ab. Mathematisch kannst du das zunächst so formulieren:

$ y = A\cdot \sin(\frac{2\cdot \pi}{\lambda}\cdot (x-c(t))) $

Nach einer Periodendauer $T$ ist die verschobene Welle wieder identisch mit der Ausgangswelle. Innerhalb dieser Zeit legt sie die Wellenlänge $\lambda$ zurück. Es gilt daher:

$ v=\frac{\lambda}{T} $

In einer beliebigen Zeit $t$ legt sie also die Strecke von $c(t)=v\cdot t=\frac{\lambda}{T}\cdot t$ zurück.

Jetzt kannst du die Gleichung der sich bewegenden Welle komplett aufschreiben. Sie hängt vom Ort $x$ und der Zeit $t$ ab:

$ f(x;t) = A\cdot \sin(\frac{2\cdot \pi}{\lambda}\cdot (x-\frac{\lambda}{T}\cdot t)) $

Was sind Differenzialgleichungen?

Bei einer normalen Gleichung wird oft eine oder mehrere Zahlen $x$ gesucht, die die Gleichung erfüllt. Bei Differenzialgleichungen werden nicht Zahlen, sondern Funktionen gesucht. Das kann zum Beispiel so aussehen:

$ f(x) = f^\prime (x) $

Gesucht sind also alle Funktionen, die mit ihrer ersten Ableitung übereinstimmen. Die $e$-Funktion erfüllt diese Bedingung.

Wenn eine Funktion von mehreren Variablen abhängt, so kann diese partiell, also in Teilen abgeleitet werden. Dafür sieh dir die Funktion $f(x;t)=2\cdot x + t$ an. Leitest du diese nach $x$ ab, dann stell dir vor, $t$ sei eine konkrete Zahl. Die partielle Ableitung nach $x$ wird als $f_x$ bezeichnet:

$ f_x = 2 $

Für die partielle Ableitung nach $t$ ist $x$ konstant:

$ f_t = 1 $

Diese Funktion würde also z. B. folgender partiellen Differenzialgleichung genügen:

$ 2\cdot f_t = f_x $

Tatsächlich erfüllen Wellenfunktionen eine bestimmte partielle Differenzialgleichung. Diese kannst du über die partiellen Ableitungen der vorher aufgestellten Wellenfunktion herleiten.

Die Wellengleichung

Die Wellenfunktion

$ f(x;t) = A\cdot \sin(\frac{2\cdot \pi}{\lambda}\cdot (x-\frac{\lambda}{T}\cdot t)\\ $

kannst du mit der Wellenzahl $k:=\frac{2\cdot\pi}{\lambda}$ und der Kreisfrequenz $\omega = \frac{2\cdot\pi}{T}$ einfacher schreiben:

$ f(x;t) = A\cdot \sin(k\cdot x-\omega t) $

Diese wird nun zweimal partiell nach $x$ und zweimal partiell nach $t$ abgeleitet:

$ f_x = k\cdot A\cdot cos(k\cdot x-\omega t)\\ f_{xx}=-k^{2}\cdot A \cdot sin(k\cdot x-\omega t)\\ \\ f_t = -\omega\cdot A\cdot cos(k\cdot x-\omega t)\\ f_{tt}=-\omega^{2}\cdot A \cdot sin(k\cdot x-\omega t) $

Dabei kannst du erkennen, dass die zweiten partiellen Ableitungen fast mit der Ausgangsfunktion übereinstimmen:

$ f_{xx}=-k^{2}\cdot f(x,t))\\ f_{tt}=-\omega^{2}\cdot f(x,t) $

Stellst du die Gleichungen nach $f(x,t)$ um und setzt sie anschließend gleich, erhältst du folgenden Ausdruck:

$ \frac{1}{k^{2}}\cdot f_{xx}=\frac{1}{\omega^{2}}\cdot f_{tt} $

Alle Funktionen $h$ der Form

$ h(x,t)= f(x+vt)+g(x-vt) $

mit zweimal partiell differenzierbaren beliebigen Funktionen $f$ und $g$ genügen dieser partiellen Differentialgleichung. Sie können eine eindimensionale Welle mit der Ausbreitungsgeschwindigkeit $v$ darstellen.

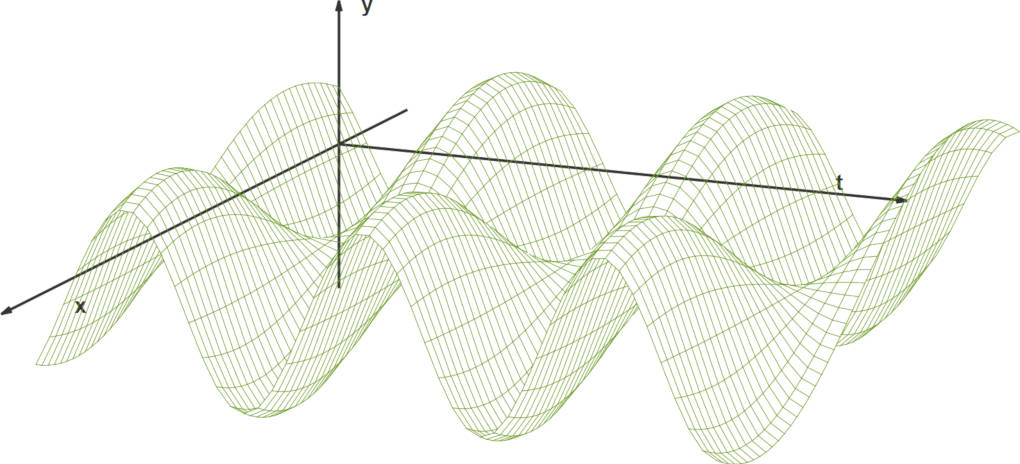
Beispiel: Wird für $f$ die Sinus- und für $g$ die Kosinusfunktion gewählt sowie $v=6\frac{m}{s}$, so ergibt sich folgende Funktion $h$:

$ h(x,t)= sin(x-6y)+cos(x+6y) $

Ihr Graph sieht im zeitlichen und räumlichen Verlauf wie folgt aus: